Ядро линейного преобразования

A.

Сравнивая это равенство с равенством (4), получаем:

,

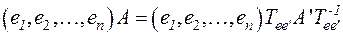откуда 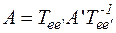и .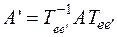

Две квадратные матрицы А и В порядка п называются подобными, если существует такая квадратная невырожденная матрица Т того же порядка, что 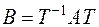. При этом обычно говорят, что матрица В получается путем трансформирования матрицы А с помощью матрицы Т.

Итак, при переходе к новому базису матрица А линейного преобразования A трансформируется с помощью матрицы Т перехода к новому базису.

Ранее мы охарактеризовали подпространство конечномерного пространства как линейную оболочку. Но возможны и другие истолкования подпространства.

Пусть, 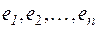– какой-либо базис пространства 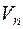, 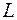– множество векторов, координатные строки, которых в базисе 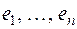образуют всевозможные решения заданной системы линейных однородных уравнений:

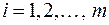, (1)

Легко убедиться, что L образует подпространство пространства V _n.

Условимся такое подпространство L называть подпространством, заданным системой уравнений (1), а базис подпространства решений системы (1) — фундаментальной системой решений.

Оказывается, что всякое подпространство может быть задано некоторой системой линейных однородных уравнений.

Введем понятия ядра линейного преобразования пространства V _n, понятия, тесно связанного с системой линейных однородных уравнений. В дальнейшем мы будем предполагать для большей простоты выводов, что число т уравнений системы (1) равно числу п неизвестных; если бы было 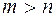, то некоторые уравнения системы (1) были бы следствиями остальных, и мы могли бы часть уравнений отбросить так, чтобы получилась система из п уравнений, равносильная первоначальной; если бы было 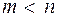, то мы могли бы добавить к системе (1) такие уравнения, чтобы получилась система из п уравнений, равносильная первоначальной.

Итак, пусть A — произвольное линейное преобразование пространства V _n, заданное в базисе 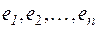матрицей п-го порядка. Назовем ядром линейного преобразования A множество всех векторов х, для которых A .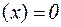

Будем обозначать ядро: Ker A: .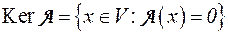

Обозначим через 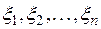координаты вектора х и через координаты образа A 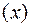(при данном базисе). Ранее мы получили, что 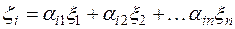, . Следовательно, вектор х тогда и только тогда принадлежит ядру линейного преобразования A 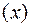, когда его координатная строка является решением системы линейных однородных уравнений , .

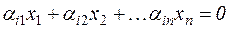Мы видим отсюда, что ядро линейного преобразования A представляет собой подпространство, заданное системой линейных однородных уравнений с матрицей А.

Образом линейного преобразования A, называется множество:

.

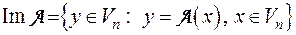Отметим некоторые свойства:

1. Ker A – подпространство и Im A – подпространство.

Если их линейная комбинация содержится в ядре:

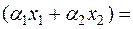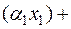A 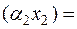A A 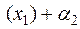A A 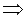принадлежит ядру.

2. Два вектора имеют один образ 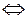их разность принадлежит ядру:

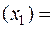A 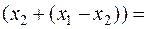A A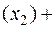

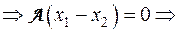
3. Отображение A инъективно тогда и только тогда, когда ядро A состоит из нулевого вектора (то есть любые неравные векторы имеют разные образы при отображении A).

4. A сюръективно: . (образ = пространству).

5. Для того чтобы A было изоморфизмом необходимо и достаточно, чтобы 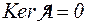, а .

Теорема 1. Если ранг матрицы А, задающей линейное преобразование A в базисе 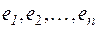пространства 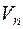, равен 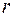, то размерность ядра равна : .

(Отсюда вытекает, что матрица линейного преобразования имеет один и тот же ранг при любом базисе пространства V _n. Благодаря этому ранг матрицы А называют также рангом линейного преобразования пространства.)

Доказательство. Для случая r = n теорема очевидна. В этом случае система линейных однородных уравнений с матрицей А будет иметь нулевое решение, поэтому ядро будет нулевым. В случае r = 0 теорема также очевидна: здесь равенство A 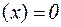выполняется для любого вектора х, вследствие чего ядро совпадает с V _n.

Пусть 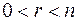. Обозначим ядро через 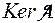= L и предположим для определенности, что неравный нулю минор А порядка r находится в левом верхнем углу матрицы А. Тогда образы 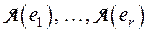_г первых r векторов базиса будут линейно независимы, так как первые r столбцов матрицы А линейно независимы. Возьмем из ядра L произвольную линейно независимую систему векторов . Покажем, что система векторов 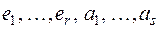также линейно независима.

Пусть имеет место соотношение

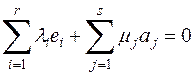, где 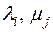– числа.

Тогда

или пользуясь соответствующими свойствами линейного преобразования:

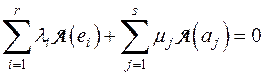, но , так как 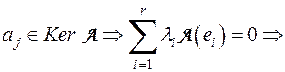в силу линейной независимости 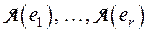, все = 0 и соотношение будет иметь вид 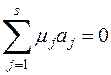. Но это возможно (вследствие линейной независимости 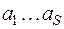) только когда все .

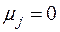В n -мерном пространстве максимальное число линейно независимых векторов равно n, так как .

Покажем, что в ядре существует хотя бы одна линейно независимая система, состоящая из k = n-r векторов.

Так как минор, не равный нулю лежит в левом верхнем углу матрицы А, то мы можем ограничиться первыми r уравнениями системы, задающей подпространство :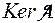

, ,

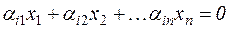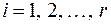где неизвестные 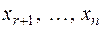, являются свободными. Придавая свободным неизвестным произвольные числовые значения, получим соответствующие значения для главных неизвестных .

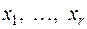Так действуя мы получим бесконечное множество решений. Рассмотрим такие k решений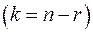

, (*)

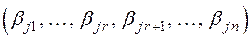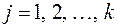чтобы определитель k-го порядка: .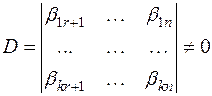

Пусть, например, 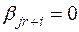при , тогда

.

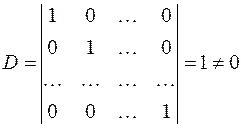Система решений (*) – линейно независима, так как матрица решений (*) имеет ранг равный k.

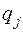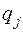Пусть – вектор, координатная строка которого . Следовательно, принадлежит 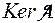и система векторов 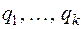– линейно независима, так как система решений линейно независима.

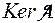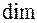
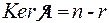Итак, в – имеется максимальное число линейно независимых векторов: , то есть , а 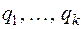– образуют базис ядра ■.

Пример: Подпространство 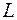четырёхмерного вещественного пространства, задается системой уравнений:

.

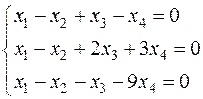Найти базис подпространства .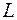

Решение.

1. Найдем ранг матрицы:

~

;

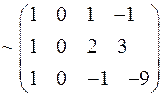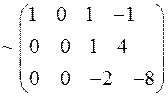
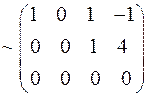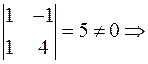ранг = 2.

Таким образом третье уравнение можно отбросить и считать свободными неизвестные 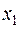и :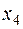

.

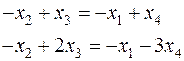Пусть .

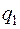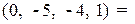
Получим решения: (1, 1, 0, 0) = ; , которые образуют фундаментальную систему решений, т.к. определитель составленный из значений свободных неизвестных 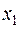и 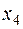: 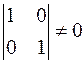. Итак векторы 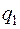и образуют базис подпространства 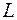, а размерность dim 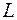=2.

Обращаем внимание на то, что если ранг матрицы А системы линейных однородных уравнений равен числу п неизвестных, то фундаментальной системы решений не существует, так как в этом случае получается только нулевое решение, которое не может быть линейно независимым.

Теперь мы можем доказать следующую теорему.

Теорема 2. Всякое подпространство пространства 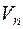может быть задано как множество решений некоторой системы линейных однородных уравнений.

Доказательство. Для нулевого подпространства утверждение очевидно – такое подпространство можно задать системой линейных однородных уравнений с п неизвестными ранга п. Утверждение очевидно и для несобственного подпространства — все пространство 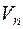можно задать системой линейных однородных уравнений с п неизвестными с коэффициентами, равными нулю. Поэтому следует рассмотреть случай, когда L ненулевое подпространство размерности 0 < т < п. Пусть базис 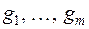подпространства L следующим образом выражается через базис 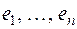пространства :

. .

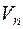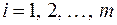Составим систему линейных однородных уравнений:

(*)

коэффициентами i-ro уравнения этой системы являются координаты вектора 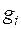. В силу линейной независимости векторов 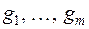их координатные столбцы

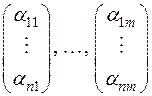
также линейно независимы и потому ранг системы линейных уравнений (*) равен т. Отсюда система линейных однородных уравнений должна обладать фундаментальной системой 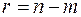решений:

.

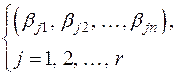Мы утверждаем, что система линейных однородных уравнений

(**)

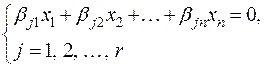как раз и задает подпространство L.

Действительно, ранг системы уравнений (**) равен, очевидно, r, и координатные столбцы являются решениями этой системы. Так как столбцы линейно независимы и их число равно 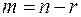, то отсюда следует, что столбцы образуют фундаментальную систему решений системы линейных однородных уравнений (**).

Таким образом, векторы 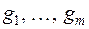образуют базис подпространства заданного системой уравнений (**), и в то же время они образуют базис L. Тем самым подпространства L и должны совпадать, что и требовалось доказать ■.

Пример. Рассмотрим трехмерное пространство 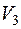геометрических векторов, имеющих начало в точке О прямоугольной системы координат OXYZ. В качестве базиса возьмем векторы 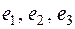, лежащие соответственно на осях OX, 'OY, OZ, имеющие положительные направления, и с длинами, равными единице. Двумерное подпространство L пространства 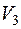будет задаваться системой линейных однородных уравнений ранга 1 или, если ограничиться линейно независимыми уравнениями, одним линейным однородным уравнением 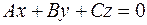. Из аналитической геометрии известно, что такое уравнение есть уравнение плоскости, проходящей через начало О прямоугольной системы координат. Мы видим, что двумерное пространство L представляет собой множество геометрических векторов, исходящих из точки О и лежащих на одной плоскости.

Аналогичным образом получается, что одномерное подпространство пространства 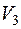представляет собой множество геометрических векторов, исходящих из точки О и лежащих на одной прямой, проходящей через О, и это подпространство задается системой двух линейных однородных уравнений с тремя неизвестными.

В аналитической геометрии всякая плоскость в пространстве задается линейным (в общем случае неоднородным) уравнением относительно текущих координат х, у, z. В теории линейных пространств аналогичную роль играет так называемое линейное многообразие или гиперплоскость.

Дата добавления: 2015-05-29