
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Простейшие свойства линейного преобразования
|
|
|
|
1. Линейное преобразование A пространства V переводит всякую линейную комбинацию векторов 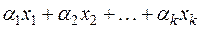 в линейную комбинацию
в линейную комбинацию  A
A 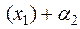 A
A 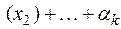 A
A 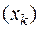 их образов с теми же коэффициентами из поля Р.
их образов с теми же коэффициентами из поля Р.
Доказательство. Сперва убедимся в справедливости утверждения для случая k=2:
A 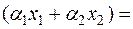 A
A 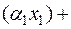 A
A 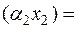
 A
A 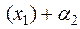 A
A 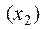
Теперь, предполагая, что утверждение доказано для k-1, где 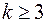 , докажем это для k векторов.
, докажем это для k векторов.
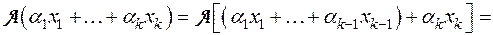
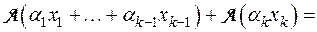
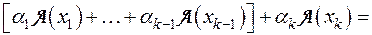
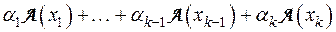 ■.
■.
2. Если A — линейное преобразование пространства V, то 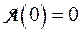 ,
, 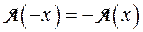 , т. е. при линейном преобразовании A образом нулевою вектора является нулевой вектор, а образом противоположного вектора –х является вектор –
, т. е. при линейном преобразовании A образом нулевою вектора является нулевой вектор, а образом противоположного вектора –х является вектор –  противоположный образу
противоположный образу  .
.
Доказательство.
Так как A - линейное преобразование пространства V, то 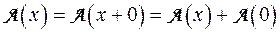 , откуда
, откуда 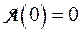 . Точно так же, рассматривая равенство
. Точно так же, рассматривая равенство 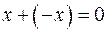 , получаем:
, получаем: 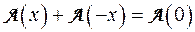 , но
, но 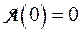 . Следовательно,
. Следовательно, 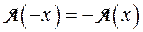 ■.
■.
3. Совокупность L всех образов  векторов х линейного пространства V, получающихся при данном линейном преобразовании, есть некоторое подпространство.
векторов х линейного пространства V, получающихся при данном линейном преобразовании, есть некоторое подпространство.
Доказательство. Возьмем из L два произвольных вектора 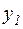 и
и 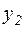 и возьмем произвольное число α из поля Р. Достаточно убедиться, что
и возьмем произвольное число α из поля Р. Достаточно убедиться, что 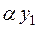 и
и 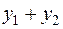 принадлежат L. Т.к.
принадлежат L. Т.к. 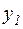 и
и 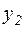 являются образами некоторых векторов
являются образами некоторых векторов  и
и 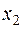 , то
, то 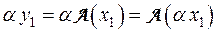 и
и  ,т.е.
,т.е. 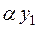 и
и 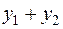 представляют собой образы векторов
представляют собой образы векторов 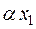 и
и 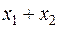 , в силу чего
, в силу чего 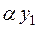 и
и 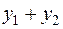 . принадлежат L ■.
. принадлежат L ■.
До сих пор линейное пространство V предполагалось как конечномерным, так и бесконечномерным. Ограничиваясь теперь n -мерным линейным пространством V n покажем, что линейное преобразование такого пространства тесно связано с квадратными матрицами n -го порядка и с линейными преобразованиями n неизвестных.
Пусть 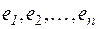 некоторый базис пространства V n и A – линейное преобразование V n. Образы A (
некоторый базис пространства V n и A – линейное преобразование V n. Образы A ( ) векторов базиса, очевидно, должны выражаться через базис:
) векторов базиса, очевидно, должны выражаться через базис:
 i = 1, 2, …, п,
i = 1, 2, …, п,
где 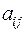 - число из поля Р. Составим квадратную матрицу n -го порядка:
- число из поля Р. Составим квадратную матрицу n -го порядка:
|
|
|
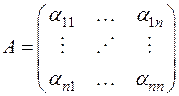
столбцы которой являются координатными столбцами соответствующих образов векторов базиса. Эту матрицу А мы будем называть матрицей линейного преобразования A в данном базисе 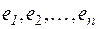 и будем также говорить, что линейное преобразование A в данном базисе
и будем также говорить, что линейное преобразование A в данном базисе 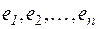 задается матрицей А. Таким образом, при данном базисе каждому линейному преобразованию A пространства V n соответствует однозначно определенная квадратная матрица А порядка п.
задается матрицей А. Таким образом, при данном базисе каждому линейному преобразованию A пространства V n соответствует однозначно определенная квадратная матрица А порядка п.
Покажем, что это соответствие является не только однозначным, но и взаимно однозначным. Предварительно докажем следующую теорему:
Теорема 1. Для произвольно заданной системы п векторов 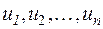 существует одно и только одно линейное преобразование A пространства V n, переводящее векторы базиса
существует одно и только одно линейное преобразование A пространства V n, переводящее векторы базиса 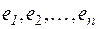 соответственно в векторы
соответственно в векторы 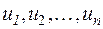 .
.
Доказательство. Возьмем произвольный вектор
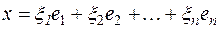 поставим ему в соответствие вектор
поставим ему в соответствие вектор  обозначим это соответствие через A и покажем, что оно является линейным преобразованием пространства V n. Прежде всего очевидно, что A есть преобразование V n. Остается доказать, что преобразование A линейно.
обозначим это соответствие через A и покажем, что оно является линейным преобразованием пространства V n. Прежде всего очевидно, что A есть преобразование V n. Остается доказать, что преобразование A линейно.
Умножим вектор х на произвольное число α из поля P 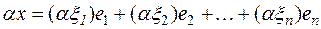 . Согласно введенному соответствию имеем
. Согласно введенному соответствию имеем
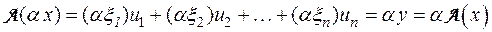 .
.
Возьмем еще один вектор 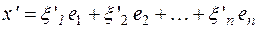 . Образом этого вектора является, очевидно,
. Образом этого вектора является, очевидно, 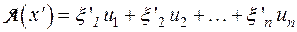 . Составим сумму
. Составим сумму  .
.
Отсюда получается, что
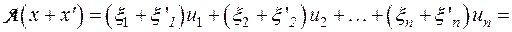
 .
.
Итак, A — линейное преобразование пространства V n. Покажем, что 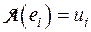 . Обратимся к равенству
. Обратимся к равенству
 =
= 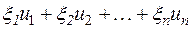 .
.
и положим 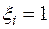
 при
при 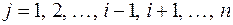 , тогда получим, что A
, тогда получим, что A 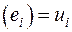 , i = 1, 2, …, п.
, i = 1, 2, …, п.
Для завершения доказательства теоремы остается убедиться в единственности линейного преобразования A, переводящего каждый вектор 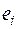 базиса в соответствующий вектор
базиса в соответствующий вектор  . Пусть имеется еще одно линейное преобразование A’ пространства V n, переводящее вектор
. Пусть имеется еще одно линейное преобразование A’ пространства V n, переводящее вектор 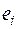 в
в  :
: 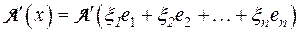 =
= 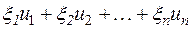 . Тогда для произвольного вектора х получаем, пользуясь свойством 1 линейного преобразования:
. Тогда для произвольного вектора х получаем, пользуясь свойством 1 линейного преобразования: 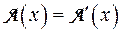 , для любого вектора х, аэто означает, что линейные преобразования A и A’ равны ■.
, для любого вектора х, аэто означает, что линейные преобразования A и A’ равны ■.
|
|
|
Теорема 2. Д ля всякой квадратной матрицы порядка п с элементами из поля Р существует одно и только одно такое линейное преобразование A пространства V n, которое в данном базисе 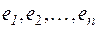 задается этой матрицей А.
задается этой матрицей А.
Доказательство. Составим систему векторов 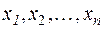 , координатные столбцы которых являются соответствующими столбцами матрицы А:
, координатные столбцы которых являются соответствующими столбцами матрицы А:  , где
, где  ,
, 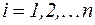 .
.
На основании теоремы 1 мы можем построить линейное преобразование A пространства V n, переводящее 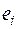 в
в 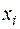 :
: 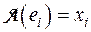 ,
, 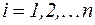 , и такое преобразование будет единственным. Очевидно, что это линейное преобразование A будет задаваться матрицей А в базисе
, и такое преобразование будет единственным. Очевидно, что это линейное преобразование A будет задаваться матрицей А в базисе 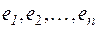 ■.
■.
Итак, мы установили взаимно однозначное соответствие (при заданном базисе) между множеством Ω всех линейных преобразований пространства V n и множеством М всех квадратных матриц n -го порядка с элементами из поля Р.
Пример. Рассмотрим двумерное пространство V2 геометрических векторов на плоскости, исходящих из начала прямоугольной системы XOY. В качестве базиса возьмем векторы 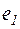 и
и 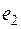 с длиною, равной единице, лежащие соответственно на осях ОХ и OY и направленные в положительную сторону. Поставим в соответствие каждому вектору х его проекцию у на прямую, проходящую через начало О и образующую с осью ОХ угол в 60°. По свойствам проекции это преобразование
с длиною, равной единице, лежащие соответственно на осях ОХ и OY и направленные в положительную сторону. Поставим в соответствие каждому вектору х его проекцию у на прямую, проходящую через начало О и образующую с осью ОХ угол в 60°. По свойствам проекции это преобразование  является линейным. Найдем матрицу этого преобразования A в базисе
является линейным. Найдем матрицу этого преобразования A в базисе 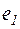 и
и 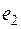 . Пользуясь некоторыми очевидными геометрическими соображениями, получаем, что конец вектора
. Пользуясь некоторыми очевидными геометрическими соображениями, получаем, что конец вектора  имеет своими координатами
имеет своими координатами  . Аналогичным образом находим, что конец вектора
. Аналогичным образом находим, что конец вектора  имеет своими координатами
имеет своими координатами 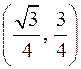 .
.
Следовательно,
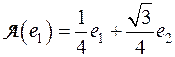 ,
, 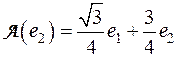
откуда A в базисе  задается матрицей
задается матрицей
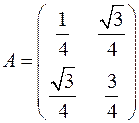 .
.
Посмотрим, как выражаются координаты образа 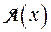 через координаты прообраза х при линейном преобразовании A пространства V n. Для этой цели введем следующее обозначение. Пусть
через координаты прообраза х при линейном преобразовании A пространства V n. Для этой цели введем следующее обозначение. Пусть
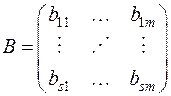
некоторая прямоугольная (в частности, квадратная) матрица, элементы которой уже не числа, а векторы пространства V n. Мы будем через A (B) обозначать матрицу
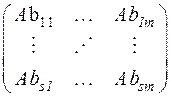
элементы которой являются образами соответствующих элементов матрицы В при линейном преобразовании 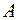 . Докажем следующую лемму.
. Докажем следующую лемму.
Лемма. Если  числовая матрица, состоящая из т строк, а В — вышеупомянутая «векторная» матрица из s строк и т столбцов, то
числовая матрица, состоящая из т строк, а В — вышеупомянутая «векторная» матрица из s строк и т столбцов, то
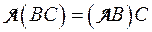
где 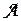 — линейное преобразование пространства V n.
— линейное преобразование пространства V n.
|
|
|
Доказательство. Пользуясь правилом перемножения
матриц, получаем, что
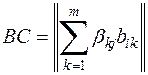
Отсюда
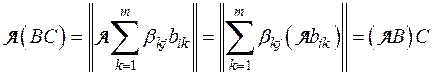 .
.
что и требовалось доказать ■.
В силу самого определения матрицы А линейного преобразования мы можем написать, что
A 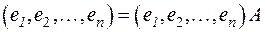 (1)
(1)
где 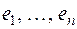 — базис V n. Возьмем теперь произвольный вектор
— базис V n. Возьмем теперь произвольный вектор
 .
.
Тогда для его образа A (х) получается на основании леммы, что

или, пользуясь равенством (1)
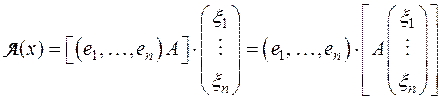 .
.
С другой стороны, обозначая координаты образа A (х) через  имеем
имеем 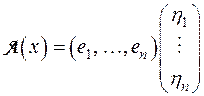 .
.
Откуда следует, что 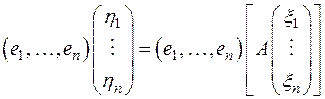 ,
,
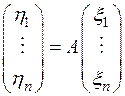 (2)
(2)
т. е. координатный столбец образа  , равен произведению матрицы А линейного преобразования A в данном базисе на координатный столбец прообраза х.
, равен произведению матрицы А линейного преобразования A в данном базисе на координатный столбец прообраза х.
Из равенства (2) получается, что
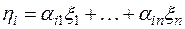 ,
,  ,
,
т. е. линейное преобразование A пространства V n вызывает линейное преобразование координат 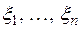 произвольного вектора x в координаты
произвольного вектора x в координаты  его образа
его образа 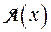 , причем матрицей этого линейного преобразования координат является А.
, причем матрицей этого линейного преобразования координат является А.
Вообще говоря, при переходе к другому базису матрица линейного преобразования пространства V n изменяется. Найдем, по какому закону изменяется при этом матрица линейного преобразования.
Пусть 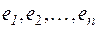 и
и 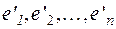 — два каких-нибудь базиса пространства V n,
— два каких-нибудь базиса пространства V n,  — матрица перехода от первого базиса ко второму,
— матрица перехода от первого базиса ко второму, 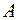 – матрица линейного преобразования A пространства V n в первом базисе и
– матрица линейного преобразования A пространства V n в первом базисе и 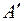 — матрица того же линейного преобразования A в во втором базисе. Тогда имеют место следующие равенства:
— матрица того же линейного преобразования A в во втором базисе. Тогда имеют место следующие равенства:
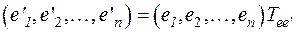 (3)
(3)
A 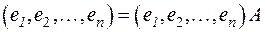 (4)
(4)
A  (5)
(5)
Подставляя в обе части равенства (5) выражение 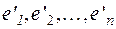 из равенства (3), получаем:
из равенства (3), получаем:
A 
или, пользуясь доказанной выше леммой:
A [ 
 .
.
Умножим обе части последнего равенства справа на обратную матрицу 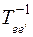 :
:
|
|
|
|
|
Дата добавления: 2015-05-29; Просмотров: 1974; Нарушение авторских прав?; Мы поможем в написании вашей работы!