Линейное преобразование пространства

В тесной связи с линейными преобразованиями неизвестных (переменных) находятся так называемые линейные преобразования линейного пространства или линейные операторы. Понятие оператора играет важную роль в различных областях математики.

Пусть V – линейное (конечномерное или бесконечномерное) пространство над числовым полем Р и пусть каждому вектору х, этого пространства ставится в соответствие вполне определенный вектор у того же пространства. Мы будем у называть образом вектора х, а вектор х — прообразом, вектора у. Обозначая соответствие через A, мы часто будем записывать образ вектора х в виде . Отметим, что соответствие A хотя и является однозначным, но может быть и не взаимно однозначным: каждый вектор x должен обладать вполне определенным образом у = , но один и тот же образ может получаться и для различных прообразов. Отметим еще, что образы могут не исчерпывать всех векторов пространства V.

Такое соответствие A называется преобразованием линейного пространства V или оператором. В частности, соответствие называется линейным преобразованием (или линейным оператором) пространства V, если оно обладает следующими двумя свойствами:

1. , т. е. образ произведения произвольного вектора х на любое число α, из Р равен произведению образа на.то же самое число α.

2. - образ суммы двух произвольных векторов x₁ и x₂ равен сумме их образов.

Примеры.

1. Рассмотрим трехмерное пространство V₃ геометрических векторов имеющих начало в одной и той же точке О. Поставим в соответствие каждому такому вектору его проекцию на координатную плоскость XOY прямоугольной системы XYZ и обозначим это соответствие, как и выше, через A. Из векторной алгебры известно, что если x₁ и x₂ — произвольные векторы V₃, α – произвольное вещественное число, то проекция произведения α x₁ равна проекции вектора x₁ умноженной на число α, а проекция суммы x₁+x₂ равна сумме проекций векторов x₁ и x₂. Таким образом,рассматриваемое преобразование A пространства V₃ является линейным.

2. Рассмотрим пространство V многочленов от х с вещественными коэффициентами и возьмем в качестве преобразования этого пространства оператор дифференцирования: D (f(x))= 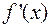, где 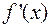— производная многочлена f(x). В силу известных свойств дифференцирования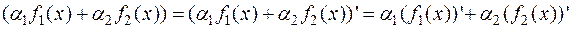: D =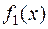

= D + D 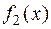т. е. оператор дифференцирования является линейным преобразованием пространства V.

3. Если обратиться к пространству вещественных функций вещественного аргумента х, бесконечно дифференцируемых на отрезке 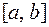, то и здесь оператор дифференцирования оказывается линейным преобразованием пространства.

4. Пусть V – произвольное (конечномерное или бесконечномерное) линейное пространство над числовым полем Р. Рассмотрим преобразование пространства V, ставящее в соответствие каждому вектору х тот же самый вектор х. Это так называемое тождественное или единичное преобразование, и мы его обозначим через Е: Е (х)= x. Легко проверить, что Е является линейным преобразованием пространства V.

5. Далее, для того же пространства V рассмотрим преобразование O, ставящее в соответствие каждому вектору x нулевой вектор O х = 0. Это так называемое нулевое или тривиальное преобразование. Нетрудно проверить, что оно является линейным преобразованием пространства V. '

Отметим простейшие свойства линейного преобразования пространства V.

Дата добавления: 2015-05-29