Обратные преобразования

Пусть и 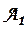— два линейных преобразования пространства 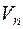. Назовем преобразование 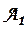обратным относительно , если 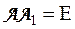. Обратное преобразование 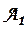мы будем обозначать через .

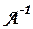Назовем линейное преобразование невырожденным, если оно в некотором базисе задается невырожденной матрицей.

Легко заметить, что невырожденное преобразование в любом базисе должно задаваться невырожденной матрицей, так как ранг матрицы линейного преобразования не зависит от выбора базиса.

Теорема. В кольце Q тогда и только тогда существует обратное преобразование 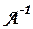для линейного преобразования , когда невырожденное. При этом обратное преобразование задается в том же базисе обратной матрицей .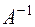

Доказательство. Пусть — невырожденное преобразование. Тогда оно задается невырожденной матрицей А, для которой существует обратная матрица 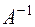. В том же базисе матрица 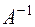будет задавать некоторое линейное преобразование 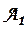. Так как 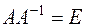, где Е — единичная матрица n -го порядка, то в силу изоморфизма между кольцом Q и кольцом М будут выполняться и равенства 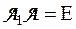, откуда .

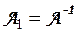Обратно, пусть для линейного преобразования существует в кольце Q обратное преобразование 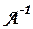. Тогда если задается матрицей А и 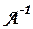задается матрицей 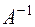то в силу изоморфизма между кольцом Q и кольцом М равенству 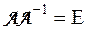должно соответствовать равенство 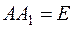, откуда 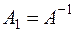, и матрица А является невырожденной, в силу чего и линейное преобразование невырожденное ■.

литература

1. Ван дер Варден Б.Л. Алгебра. - СПб.: Лань, 2004. - 624 с.

2. Привалов И.И. Аналитическая геометрия. - СПб.; М.; Краснодар: Лань, 2007. - 304 с.

3. Цубербиллер О.Н. Задачи и упражнения по аналитической геометрии. - СПб.: Лань, 2003. - 336 с.

4. Фаддеев Д.К., Соминский И.С. Задачи по высшей алгебре. - СПб.; М.; Краснодар: Лань, 2007. - 288 с.

5. Курош А.Г. Курс высшей алгебры. - СПб.; М.; Краснодар: Лань, физматкнига, 2007. - 432 с.

6. Окунев Л.Я. Высшая алгебра.- СПб.: Лань, 2009. - 336 с.

Содержание

1. Определение линейного векторного пространства. 3

Примеры линейных пространств: 5

Понятие подпространства. 9

2. Линейная зависимость. 11

3. Конечномерное пространство. 18

Изоморфизм линейных пространств. 21

4. Базис. 27

Связь базиса и координат вектора в пространстве. 30

Свойства матрицы перехода. 32

Подпространства. 33

5. Линейное преобразование пространства. 36

Простейшие свойства линейного преобразования. 39

6. Ядро линейного преобразования. 48

7. Линейное многообразие (гиперплоскость) 56

8. Кольцо линейных преобразований. 61

Обратные преобразования. 65

Литература. 66

Дата добавления: 2015-05-29