Свойства изоморфизмов

a) Симметрии, т. е. если пространство V изоморфно отображается на пространство V ', то и, обратно, существует изоморфное отображение пространства V ' на V.

b) Рефлексивности, т. е. пространство V изоморфно отображается на самого себя, например изоморфным отображением на себя будет соответствие, при котором образом вектора х из V является тот же вектор х (тождественное отображение).

c) Транзитивности, т. е. если пространство V изоморфно отображается на пространство V ', а V ' изоморфно отображается на пространство V '', то V может быть изоморфно отображено на V ''.

Отметим еще несколько простейших свойств изоморфизма линейных пространств.

d) При изоморфном отображении пространства V на V ' нулевой вектор 0 из V имеет своим, образом нулевой, вектор 0 ' из пространства V '.

Доказательство. Возьмем из V произвольный вектор х', он будет образом некоторого вектора х из V. Согласно определению' изоморфизма получаем, что , т. е. 0' – нулевой вектор пространства V '.

e) При изоморфном отображении пространства V на V ' образом вектора –х, противоположного вектору х из V, является вектор 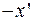, противоположный образу х' вектора х.

Доказательство.

f) При изоморфном отображении пространства V на V ' образы линейно зависимой системы векторов из V образуют также линейно зависимую систему, а образы линейно независимой системы из V также линейно независимы.

Доказательство. Возьмем какую-нибудь линейно зависимую систему векторов из V, Для нее можно указать такой ненулевой набор чисел 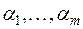из Р, что .

.

Образом правой части равенства является нулевой вектор 0' из V '. Следовательно, 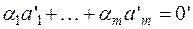. Мы видим, что система образов 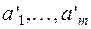линейно зависима.

Пусть теперь линейно независимая система векторов из V. Допустим, что система их образов 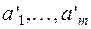линейно зависима. В силу свойств симметрии изоморфизма линейных пространств мы можем пространство V ' изоморфно отобразить на пространство V, а именно это будет отображение, при котором вектор х является образом вектора . Отсюда по доказанному выше система векторов будет линейно зависима, что противоречит линейной независимости системы ■.

Понятие изоморфизма важно тем, что два изоморфных линейных пространства алгебраически неразличимы, т. е. обладают одними и теми же свойствами относительно установленных в них операции сложения векторов и умножения вектора на число из поля Р.

Пример. Пусть V — линейное пространство квадратных матриц порядка n над числовым полем Р и – пространство n² -мерных строк над тем же полем. Поставим в соответствие матрице

из V строку из . Такое соответствие является изоморфным.

Отметим, что для изоморфных пространств может существовать несколько и даже бесконечное множество изоморфных соответствий. Так, в данном примере можно было поставить в соответствие матрице А строку 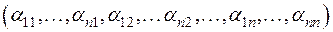и нетрудно проверить, что здесь также получается изоморфное отображение пространства V на .

Теперь, обращаясь к конечномерным пространствам, выясним, когда эти пространства изоморфны.

Теорема 1. Два линейных пространства V _n u V _m над числовым полем Р различной размерности n и т не могут быть изоморфными.

Доказательство. Предположим противное – пусть пространства V _n и V _m изоморфны, а п ≠ т. Мы можем считать в силу свойства симметрии изоморфного соответствия, что п > т и пространство V _п изоморфно отображается на пространство V_т. В пространстве V _п существует по меньшей мере одна линейно независимая система векторов . Обозначим через соответствующие образы векторов . По свойству изоморфизма система образов должна быть также линейно независима. Но это противоречит тому, что V _т – пространство размерности т < п ■.

Теорема 2. Пространство V_n (п > 1) над числовым полем Р иэоморфно пространству n-мерных строк (столбцов) над тем же полем Р.

Доказательство. Мы уже знаем, что в n -мерном пространстве V _n должен существовать по меньшей мере один базис из n векторов. Пусть таким базисом будет система векторов 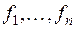. Возьмем из V _n произвольный вектор и поставим ему в соответствие координатную строку 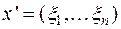при базисе 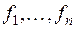. Пусть 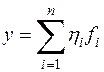еще один вектор из V _п. Очевидно, образом у будет координатная строка . В силу единственности выражения вектора через базис равенство х = у тогда и только тогда имеет место, когда 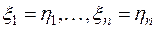, т. е. когда равны образы х' и у'. Следовательно, различные векторы пространства V '_n должны иметь при введенном нами соответствии различные образы. Далее, если 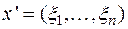– п- мерная строка с произвольным набором чисел 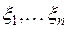из поля Р, то можно всегда указать такой вектор х пространства V _n, для которого строка 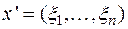будет образом, а -именно это будет вектор .

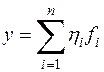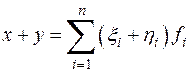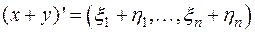Складывая векторы и , получаем, что и мы видим, что образом суммы является строка . Но по правилу сложения матриц 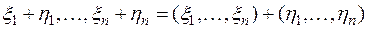. Следовательно, , т. е. образ суммы оказался равным сумме образов.

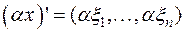Наконец, умножая вектор на произвольное число α из поля Р, получаем, что . Отсюда образом вектора является строка ). Но по правилу умножения матрицы на число 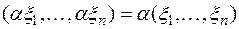. Следовательно, (ах)' =αх', т.е. образ произведения вектора на число из поля Р оказался равным произведению образа этого вектора на то же самое число.

Аналогично обнаруживается изоморфизм пространства V _n с пространством n -мерных столбцов над полем Р ■.

Из только что доказанной теоремы сразу вытекает следующая важная теорема.

Теорема 3. Два линейных пространства над числовым полем Р одинаковой размерности п (п > 1 ) изоморфны.

Доказательство. Каждое из этих двух пространств по предыдущей теореме изоморфно с одним и тем же пространством R_n – n -мерных строк над полем Р. Отсюда, пользуясь свойствами симметрии и транзитивности изоморфного отображения, получаем, что эти два пространства должны быть изоморфны:

■.

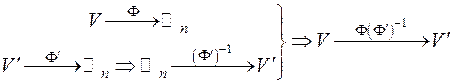Два нулевых пространства над полем Р также изоморфны, а именно: поставим в соответствие нулевому вектору одного из нулевых пространств нулевой вектор другого нулевого пространства; получим, очевидно, изоморфное соответствие.

Дата добавления: 2015-05-29