Подпространства

Пример.

Доказательство.

Свойства матрицы перехода

Пусть мы имеем три базиса в V_n:

и три матрицы перехода: , не равные между собой, тогда:

1.

Для любого =>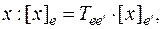

=>

■.

2. , т. е.матрица перехода от базиса к базису является единичной матрицей.

3. Пусть базис = => по первому свойству => .

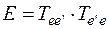Пусть 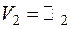, т.е. мы имеем дело с пространством двумерных строк.

Имеем базис 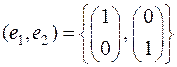; новый базис: ;

, следовательно матрица перехода:

Теорема. Ненулевое подпространство L пространства V_n над числовым полем Р также конечномерно, причем размерность т подпространства L не превосходит размерности п пространства V_n и равна п только тогда, когда L совпадает c V _n (т. е. является несобственным подпространством), т.е. 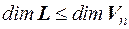, если , то 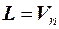, иначе .

Доказательство. Так как L — ненулевое подпространство, то в L существует хотя бы один ненулевой вектор, и тем самым в L существует по меньшей мере одна конечная линейно независимая система векторов (т ≥ 1). Так как в пространстве V _n всякая система s>n векторов линейно зависима, то m ≤ п. Возьмем в подпространстве L линейно независимую систему с максимальным числом m векторов и покажем, что такая система образует базис L.

В самом деле, присоединим к системе произвольный вектор х из L. Тогда в силу максимальности числа т мы получим линейно зависимую систему векторов:

,

где по меньшей мере одно из чисел 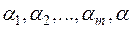, изполя Р отлично от нуля. Число 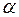должно быть отлично от нули; в противном случае получилось бы соотношение равное нулю с ненулевым набором чисел 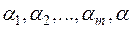, что противоречит линейной независимости системы . Но если ,значит всякий вектор х подпространства L линейно выражается через линейно независимую систему . Таким образом, система векторов образует базис подпространства L, причем размерность L равна m.

В случае т = п система векторов образует базис не только подпространства L, но и всего пространства V_n. Это следует из того, что всякая система п линейно независимых векторов – базис n -мерного пространства. Отсюда если х — некотрый вектор пространства V_n, то х будет линейно выражгься через систему а так как векгоры принадлежат L, то х, являясь линейной комбинацией , будет также принадлежать L. Следовательно, V _n должно совпадать с L.

В случае m < п подпространство L будет уже собственным, так как базис L не может быть в этом случае базисом всего пространства ■.

Из только что доказанной тесремы вытекает, что всякое подространство L пространства V_n является линейной оболочкой системы векторов .

В самом деле, если L, нулевое, то L можно рассматривать как линейную оболочку, натянутую на нулевой вектор. Если же L ненулевое, то в L существует базис и всякий вектор -x из L является линейной комбинацией . Обратно, всякая линейная комбинация векторов есть вектор, x принадлежащий L, так как принадлежат подпространству L. Следовательно, L есть линейная оболочка, натянутая на систему векторов .

Укажем еще, каким образом можно находить базис и размерность линейной оболочки L, натянутой на линейно зависимую систему векторов пространства V _n.

Пусть — координатная строка вектора , в некотором базисе пространства V _n. Составляем матрицу А размера , строками которой служат координатные строки векторов . Пусть r - ранг матрицы А и D - какой-нибудь ее минор r - гопорядка, отличный от нуля и лежащий на строках с номерами . Тогда в силу изоморфизма пространства V _n с пространством n -мерных строк получается, что ранг системы векторов равен r, подсистема векторов ,– линейно независима и остальные векторы системы линейно выражаются через эту подсистему. Отсюда любой вектор х линейной оболочки L будет линейно выражаться через , которые образуют базис L, в следствие чего размерность линейной оболочки L равна r.

Пример. Линейная оболочка L натянута на систему векторов:

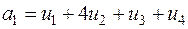
где — базис вещественного пространства V₄; Найти базис и размерность линейной оболочки L.

Решение. Составляем матрицу А, строками которой служат координатные строки векторов . Получаем матрицу:

, найдём её ранг

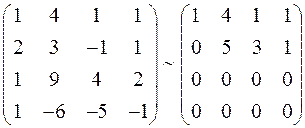, т.е. ранг =2

Мы нашли, что ранг этой матрицы равен двум, ее первые две строки линейно независимы. Следовательно, векторы 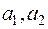образуют базис L и размерность линейной оболочки равна двум.

Дата добавления: 2015-05-29