Нестационарный теплообмен с окружающей средой

Стационарная теплопроводность двухслойной среды.

Тг > То q →

Тг ˂ То ← q

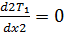0 ˂ x ˂ l (1)

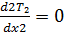l ˂ x ˂ l (2)

Поскольку имеем 2 уравнения второго порядка для конкретности (однозначности) задачи необходимо использовать граничные условия.

Т₁ (x = 0) = Tг (3)

Т₂ (x = L) = To (4)

Т₁ (х =l) = Т₂ (х = L) (5)

(6)

T₁ = c₁x + c₂; T₂ = c₃x + c₄

Постоянные с₁ – с₄ определяется системой алгебраических уравнений 3– 6.

Обозначим неизвестную t˚ через T₁ (x = c) = T₂(x = l) = T_l, тогда 4 const c₁ – c₄ можно определить из 4 условий 3 – 5 в последней неизвестную Т_l находим из 6.

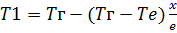(7)

(8)

Используя (7) и (8), подставляя в условие (6) получаем уравнение для нахождения неизвестной Т соприкосновения

Решая это уравнение находим Те

;

(9)

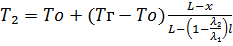(10)

;

;

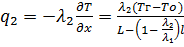q₁ = q₂.

;

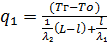l = l₁

L – l = l₂

;

;

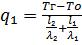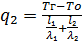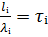
Где: τᵢ - термическое сопротивление i- того слоя.

Чем больше знаменатель,тем меньше тепловой поток; тем больше термическое сопротивление, чем больше коэффициент тепла

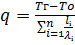
Если теплопроводность рассматриваемой среды достаточно большая, а размеры тела небольшие, то можно считать, что температура Во всех точках равна:

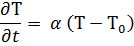
Это закон охлаждения Ньютона.

Задачи.

№1. В сосуд положили кусок льда m_л = 10 кг, Т_л = -10⁰. Найти массу воды m_в в сосуде после того как ему сообщили Q =20 МДж. Удельная теплота плавления льда L_л = 0.33 МДж/кг*К; удельная теплота парообразования r_п = 2,3 МДж/кг*К. Удельная теплоемкость воды с_в = 4,2 КДж/кг*К, льда с_л = 2,1 КДж/кг*К.

Решение:

1)Нагрев льда до 0⁰:

Q₁ = m_л * c_л * (t₀ – t_л) = 10*2100*10 = 0,21 МДж;

2)Q₂ = m_л * L = 10*0.33*10⁶ = 3.3 МДж;

3)Q₃ = m_л * c*(t - t₀) = 10*4200*100 = 4.2 МДж;

4)Q₄ = m_л * r = 10*2.3*10⁶ = 23 МДж;

Q₁ + Q₂ + Q₃ < Q < Q₁ + Q₂ + Q₃ + Q₄;

0,21+3,3+4,2 < 20 < 0.21+3.3+4.2+23

7.71 < 20 < 30.71

№2. В сосуд при 0⁰ находится вода, при быстром откачивании воздуха вода испаряется (понижается давление), оставшаяся часть воды замерзает. Удельная теплота плавления льда L=330 кДж/кг, удельная теплота испарения воды r=2300 кДж/кг. Сосуд теплоизолирован. Какая часть воды замерзнет, какая часть испарится?

Решение:

Поскольку сосуд теплоизолирован, необходимое для испарения воды тепло получается только за счет скрытой теплоты, которая выделяется при замерзании воды.

m_л*L = m_п*r;

m_л + m_п = m;

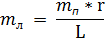
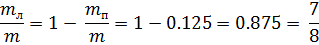
№3. В теплоизолированном сосуде при 0⁰ находится m_л = 100 г льда. Лед подвергли сжатию до давления P = 1200 атм. Известно, что при увеличении давления, температура льда понижается. Причем линейно: увеличение давления на 138 атм. Температура плавления льда понижается на 1 градус. Лед плавится до тех пор, пока его температура не опустится до Т = -8,696⁰. Удельная теплота плавления льда L=330 кДж/кг, удельная теплоемкость льда с_л = 2,1 кДж/кг*К.

Решение:

Лед плавится до тех пор, пока его температура не опуститься до -8,696⁰

Q₁ = m₁*c*ΔТ

ΔТ = 0 – (- 8,696) = 8,696⁰С

Q₂ = m₂ * L

c * m₁ * ΔТ = m₂ * L

5% льда расплавится

отсюда следует что масса расплавившегося льда m₂ = 5,6 г.

№4. В сосуд, содержащий m_в= 2 кг при температуре Т=5⁰ положили кусок льда m_л = 5 кг, Т_л = -40⁰. Найти температуру смеси по установлении равновесия. Удельная теплоемкость воды с_в = 4,2 КДж/кг*К, льда с_л = 2,1 КДж/кг*К. Удельная теплота плавления льда L=330 кДж/кг.

Решение:

Возможны три случая:

1)весь лед растает и температура воды станет больше 0⁰C

2)вся вода замерзнет и температура льда будет ниже 0⁰C

3)смесь льда и воды при температуре 0⁰C

Q_в = 2*4200*5 = 42000 Дж

Q_л = 5*2100*40 = 420000 Дж

Q_c = m_л * L = 330*5 = 1650 Дж

Q_в + Q_c > Q_л

42000 < 421650

Количество теплоты выделенное при охлаждении воды до 0⁰C равна 42000 Дж

9,9 % льда растает.

Так как Q_в < Q_л поэтому 1 и 2 случаи не реализуются.

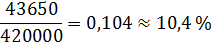
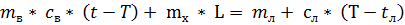
№5. В сосуд, содержащий смесь воды m_в = 500 г, m_л = 54 г при температуре T₀ = 0⁰. В сосуд вводится пар m_п = 6,6 г, пар сухой, насыщенный, при температуре Т_п = 100⁰. Найти температуру после установления равновесия. Удельная теплоемкость воды с_в = 4,2 КДж/кг*К.. Удельная теплота плавления льда L_л=330 кДж/кг. Удельная теплота парообразования r_п = 2,3 МДж/кг*К.

Решение:

Q_в = 0.5*4200*ΔT_в = 2100 ΔT_в;

Q_л = 0,0544*2100* ΔT_л = 114,24 ΔT_л;

Q_п = 0,0066*100*4200 = 2772 Дж;

При Т=100⁰

Q = m_п * r + m_п * c_в * ΔT = 0,0066*2300 + 0,0066*4200 *100 = 18 кДж;

В сосуде при 0⁰С останется только вода, весь лед расплавится.

m_в = 500+54.4+6.6 = 561 г.

Дата добавления: 2015-05-26