Доведення. Нехай пряма а лежить у площині α , а пряма b перетинає цю площину в точці А такій, що А α (рис

Нехай пряма а лежить у площині α, а пряма b перетинає цю площину в точці А такій, що А α (рис. 38). Доведемо, що прямі а і b мимобіжні. Припустимо, що прямі a і b не мимобіжні, тобто вони лежать в деякій площині β. Площина β проходить через пряму а і точку А і тому збігається з площиною α. Таким чином, пряма b лежить в площині α, що супере­чить умові. Отже, прямі a і b не лежать в одній площині, що і треба було довести.

Білет № 5

1. Квадратні рівняння з від’ємним дискримінантом.

2. Конус. Осьовий переріз конуса. Переріз конуса площинами

3. Обчислити: .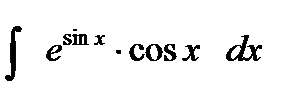

4. Основою прямого паралелепіпеда є ромб зі стороною а і гострим кутом . Менша діагональ паралелепіпеда нахилена до площини основи під кутом 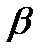. Знайдіть площу бічної поверхні паралелепіпеда.

1. Квадратні рівняння з від’ємним дискримінантом

Квадратне рівняння — це рівняння виду a x² + b x + c = 0, де a не дорівнює 0.

Для розв'язання квадратного рівняння необхідно порахувати дискримінант

D = b²- 4ac.

Якщо D > 0, то рівняння має два різних дійсних кореня: х_1,2=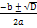

Якщо D = 0, то обидва кореня дійсні і рівні: х_1,2=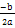

Якщо D < 0, то оба кореня комплексні числа: х_1,2=

2. Конус. Осьовий переріз конуса. Переріз конуса площинами

Прямим круговим конусом називається тіло, утворене обертанням плоского прямокутного трикутника навколо одного із його катетів .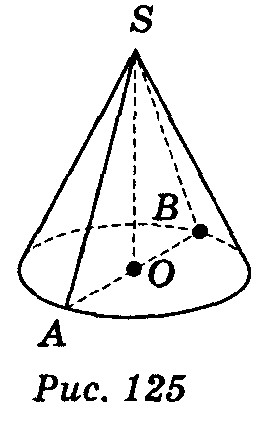

Радіус цього круга називається радіусом конуса; то­чка S, відрізок SА, відрізок SO, пряма SO називаються відповідно вершиною, твірною, висотою і віссю конуса.

Осьовий переріз конуса — переріз конуса площиною, яка проходить через його вісь. Всі осьові перерізи конуса являють собою рівнобедрені трикутники, рівні між собою.

На рис. 125 ∆SАВ — осьовий переріз (SА = SВ ).

Висотою конуса називається перпендикуляр, опущений з його вершини на площину основи. У прямого кругового конуса основа висоти збігається з центром основи.

Площина, паралельна площині основи конуса, перетинає конус по кругу, а бічну поверхню — по колу з центром на осі конуса.

Білет № 6

1. Числова функція. Область визначення та множина значень.

2. Піраміда. Види піраміди. Переріз піраміди площиною паралельною основі.

3. Знайти площу фігури, обмеженої лініями у = sin x, y = 0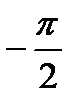, x = , x = .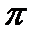

4. Через гіпотенузу прямокутного рівнобедреного трикутника проведено площину, яка утворює з площиною трикутника кут 45⁰. Знайдіть кути, які утворюють катети трикутника з цією площиною.

1. Числова функція. Область визначення та множина значень

Числовою функцією з областю визначення D називається за­лежність, при якій кожному числу х із множини D ставиться у відповідність по деякому правилу єдине число у із множини Е.

Змінна х називається незалежною змінною або аргументом функції, а змінна у — залежною змінною або функцією.

Область визначення функції позначається D(f). Множина, яка складається із всіх чисел f(x) таких, що х належить області визначення функції f, називаєть­ся областю значень функції і позначається E(f).

Областю визначення функції у = f(x), яка задана формулою, називається множина тих значень, які може приймати х, тобто формула має зміст (усі дії, вказані формулою, можна виконати). При знаходженні області визначення слід пам'ятати:

1) Якщо функція є многочленом у = а_n хⁿ + α_n-1 x^n-1 +... + α₁x + a₀,

то D(y) = (- ; + ) = R.

2) Якщо функція має вигляд у = , де f(x) і g(x) — многочлени, то слід вважати g(x)≠ 0 (знаменник дробу не дорів­нює 0).

3) Якщо функція має вигляд у = 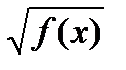, то слід вважати f(x) > 0 (арифметичний квадратний корінь існує тільки з невід'ємних чисел).

2. Піраміда. Види піраміди. Переріз піраміди площиною паралельною основі

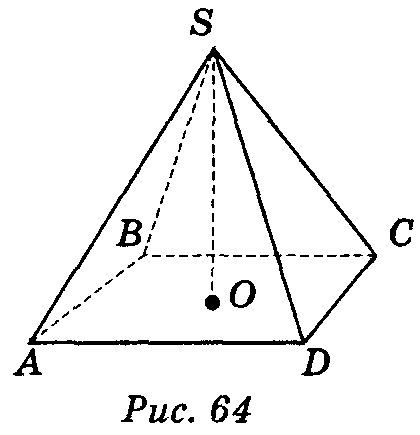n -кутною пірамідою називається многогранник, одна грань яко­го — довільний n -кутний, всі інші n граней — трикутники, що ма­ють спільну вершину.

Спільну вершину трикутних граней на­зивають вершиною піраміди, протилежну їй грань — основою, а всі інші грані — бічни­ми гранями піраміди.

Відрізки, що сполучають вершину піра­міди з вершинами основи, називають бічни­ми ребрами.

Перпендикуляр, опущений з вершини пі­раміди на площину її основи, називають ви­сотою піраміди. Висотою також називають і довжину цього перпендикуляра.

Площина, паралельна основі піраміди, розтинає її на піраміду і фігуру, яка називається зрізаною пірамідою. Піраміда, що відтинається цією площиною, подібна даній.

Грані зрізаної піраміди, що лежать у паралельних площинах, називаються основами піраміди; всі інші грані – бічні грані піраміди. Основи зрізаної піраміди – гомотетичні многокутники. Кожна з бічних граней зрізаної піраміди – трапеція.

Площина, паралельна основі піраміди, розтинає її на піраміду і фігуру, яка називається зрізаною пірамідою. Піраміда, що відтинається цією площиною, подібна даній.

Грані зрізаної піраміди, що лежать у паралельних площинах, називаються основами піраміди; всі інші грані – бічні грані піраміди. Основи зрізаної піраміди – гомотетичні многокутники. Кожна з бічних граней зрізаної піраміди – трапеція.

Білет № 7

1. Монотонність, обмеженість, парність, непарність, періодичність функцій.

2. Многогранники. Призма. Паралелепіпед та його властивості.

3. Запишіть у вигляді степеня .

4. Через вершину прямого кута В трикутника АВС до площини проведено перпендикуляр ВК, довжина якого дорівнює 7 см. Знайдіть відстань від точки К до прямої АС, якщо АС = 8 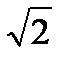см, 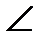ВАС = 45⁰.

1. Монотонність, обмеженість, парність, непарність, періодичність функцій

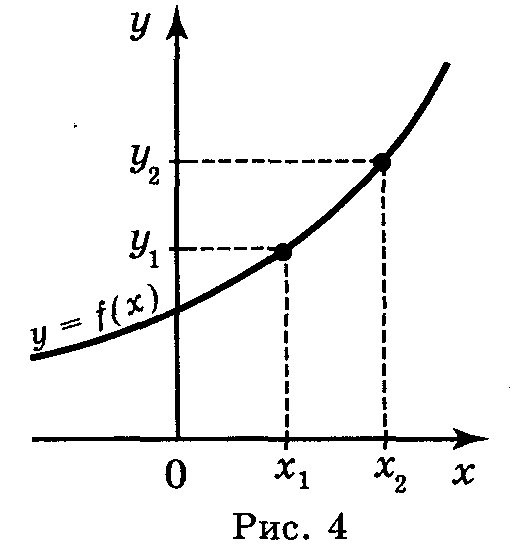Функція у = f(x) називається зростаючою (рис. 4), якщо більшому значенню аргументу відповідає більше значення функції, тобто для будь-яких значень х₁ і х₂ з області визначення функції таких, що х₁ < х₂, виконується нерівність f(x₁) < f(x₂) і навпаки: із того, що f(x₁) < f(x₂) виконується нерівність х₁ < х₂.

Функція у = f(x) називається спадною (рис. 5), якщо більшому значенню аргументу відповідає менше значення функції, тобто для будь-яких значень х ₁і х ₂з області визначення функції та­ких, що х ₁ < х ₂, виконується нерівність f(x₁) > f(x₂) і навпаки: якщо у = f(x) — спадна, то із того, що f(x₁) > f(x₂), виконується нерівність х₁ < х₂.

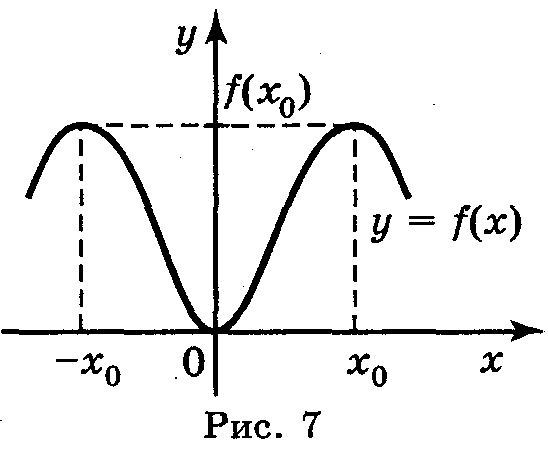
Функція у = f(x) називається парною, якщо для будь-якого значення х із D(y) значення – х також належить D(y) і виконується рівність f(-x) = f(x).

Графік парної функції симетричний відносно осі ОУ (рис. 7).

Функція у = f(x) називається непарною, якщо для будь-якого значення х із D(y) значення - х є D(y) і виконується рівність f(-x) = -f(х).

Графік непарної функції симет­ричний відносно початку координат (рис. 8).

Функція у = f(x) називається періодичною з періодом Т 0, якщо для будь-якого х із області визначення числа х + Т і х – Т також належать області визначення і виконується рівність f (x + Т) = f (x – Т) = f(x).

Приклад, період тангенса і котангенса дорівнює π, а період косинуса і синуса дорівнює 2π.

2. Многогранники. Паралелепіпед та його властивості.

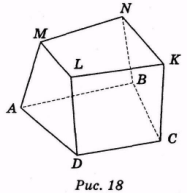
Многогранником називають тіло (частина простору), обмежене скінченою

кількістю плоских многокутників (рис. 18).

Многокутники, які обмежують многогранник, називають його гра­нями, їх сторони

— ребрами, а вершини — вершинами многогранника.

Многогранник називається опуклим, якщо він лежить по один бік від площини кожного з плоских многокутників на його поверхні.

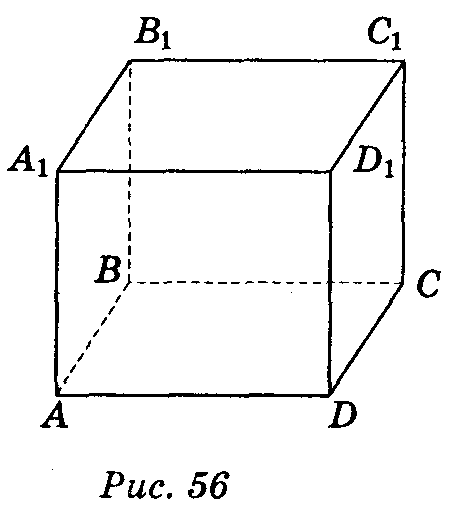Прикладами опуклих многогранників можуть бути куб, прямокут­ний паралелепіпед, тетраедр тощо.

Паралелепіпедом називається призма в основі якої лежить паралелограм.

♦ Протилежні грані паралелепіпеда паралельні та рівні.

♦ Діагоналі паралелепіпеда перетинаються в одній точці і точкою перетину діляться пополам

♦ Точка перетину паралелепіпеда є його центром симетрії.

♦ Паралелепіпед в основі якого лежить прямокутник називається прямим.

♦ У прямокутному паралелепіпеді квадрат будь-якої діагоналі дорівнює сумі квадратів трьох

його вимірів

Білет № 8

1. Найпростіші перетворення графіків функцій.

2. Поняття про статистику. Мода, медіана, середні значення.

3. Обчислити: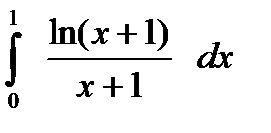

4. В циліндрі площа основи дорівнює Q, а площа осьового перерізу S. Визначити повну поверхню циліндра.

1. Найпростіші перетворення графіків функцій

№ з/п	Формула залежності	Приклад	Перетворення
	y = - f(х)		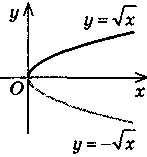Симетрія відносно осі Ох
	y = f(х) + a		Паралельне перене­сення вздовж осі Оу на а одиниць (якщо а > 0, то вгору, якщо а < 0, то вниз)
	y = f(х + a)		Паралельне перене­сення вздовж осі Ох на + а одиниць (якщо а > 0 — вліво, якщо а < 0 — вправо)
	y = kf(х) (k > 0 )		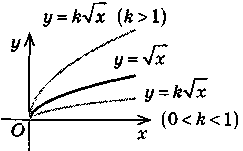Той самий вигляд, що і y = f(x), тільки розтяг-нуто, якщо k > 1, і стиснуто, якщо 0 < k < 1

2. Поняття про статистику. Мода, медіана, середні значення.

Статистика – наука, що збирає, обробляє і вивчає різні дані, пов’язані з різними масовими явищами, процесами, подіями. Предметом вивчення статистики є вивчення кількісної сторони цих явищ.

Математична статистика – розділ математики, присвячений математичним методам систематизації, обробки та дослідження статистичних даних для наукових і практичних висновків.

Статистичне спостереження – це спланований, науково організований збір масових даних про соціально-економічні явища та процеси.

Основні поняття математичної статистики

1. Статистичні дані — сукупність чисел, які дають кількісну характеристику ознак певних об'єктів та явищ, що нас цікавлять.

2. Відібрану для спостереження сукупність об'єктів називають вибірковою сукупністю або вибіркою.

3. Кількість об'єктів сукупності називають об'ємом сукупності.

4. Числа, що є значеннями ознак кожної групи, на які можна поділити вибірку, називають варіантами; послідовність варіант називають варіаційним рядом.

5. Частоти — числа, які показують, скільки разів повторювалось кожне значення ознаки сукупності.

6. Відношення частоти до об'єму вибірки називають відносною частотою.

Вибірка характеризується центральними тенденціями: середнім значенням, модою і медіаною. Середнім значенням вибірки називається середнє арифметичне всіх її значень: де x_i — значення ознаки (варіанти); п — число одиниць сукупності

Мода вибірки – те її значення, яке трапляється найчастіше. Позначається Мо.

Медіана вибірки – це число, яке “поділяє” “навпіл” упорядковану сукупність усіх значень вибірки, тобто середня величина змінюваної ознаки, яка міститься в середині ряду, розміщеного в порядку зростання або спадання ознаки. Позначається Ме.

Білет № 9

1. Числові послідовності та їх класифікація.

2. Перпендикулярність площин. Ознака перпендикулярності площин.

3. Знайдіть область визначення функції y = lg(3x – 2x² – x³).

4. Висота конуса дорівнює Н. кут між висотою та твірною дорівнює 30⁰. Обчислити площу перерізу, проведеного через дві твірні, кут між якими дорівнює 60⁰.

1. Числові послідовності та їх класифікація

Числовою послідовністю називається функція, яка задана на множині всіх натуральних чисел або на множині перших п натуральних чисел.

Числова послідовність позначається так: (а_п): а ₁; а ₂; а ₃;...; а_п.

Кожне число а_п — п- йчлен послідовності; п — номер члена.

Види числових послідовностей:

1. Якщо кількість членів п послідовності (а_п) скінченна, то (а_п) — скінченнапослідовність.

Якщо кількість членів п послідовності (а_п) нескінченна, то (а_п) — нескінченнапослідовність.

Приклади:

а) послідовність (а_п) натуральних чисел нескінченна;

б) послідовність (а_п) коренів рівняння (х – 1)(х – 2)(х + 3) = 0 скінченна.

2. Якщо кожний наступний член послідовності, починаючи з другого, більший за попередній, то послідовність є зрос­таючою.

Якщо кожний член послідовності, починаючи з другого, менший від попереднього, то послідовність є спадною.

Приклади:

а) (а_п): 1; 2; 3;... — послідовність натуральних чисел є зростаючою;

б) (b_п):-1; -2; -3;... — послідовність цілих від'ємних чисел є спадною.

Способи задання числових послідовностей:

1) описом знаходження її членів.

Приклад. Числова послідовність дільників числа 15, за­писаних у порядку зростання:

(а_п): а ₁= 1; а ₂ = 3; а ₃ = 5;...; а ₄ = 15;

2) переліком її членів.

Приклад. (а_n ): 54; 1; 33; 27, тоді а ₁ = 54; а ₂ = 1; а ₃ = 33; а ₄ = 27;

3) таблицею.

4) формулою п -го члена.

Приклад. а_п = п ²– 1, тоді а ₁= 1² – 1 = 0; а ₂ = 2² – 1 = 3; а ₃ = 3² – 1 = 8 і т.д.;

5) рекурентною формулою.

Приклад. а_п = а _{п- 1}∙ а_{п -2}, якщо а ₁ = 1; а ₂ = 2, тоді а ₁ = 1; а ₂ = 2; а ₃ = а ₁ ∙ а ₂ = 2; а ₄ = а ₂ ∙ а ₃ = 2 ∙ 2 = 4;

а ₅ = а ₃ ∙ а ₄ = 4 ∙ 2 = 8.

2. Перпендикулярність площин. Ознака перпендикулярності площин.

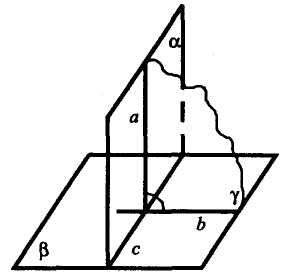Означення перпендикулярності двох площин.

Дві площини, що перетинаються, нази­ваються перпендикулярними, якщо тре­тя площина, проведена перпендикуляр­но до лінії перетину цих площин, пере­тинає їх по перпендикулярних прямих.

Якщо площина α перетинає площину β по прямій с, γ 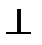с:γ перетинає α по прямій а, γперетинає β по прямій b і 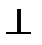а с, а 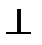b, то α 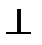β.

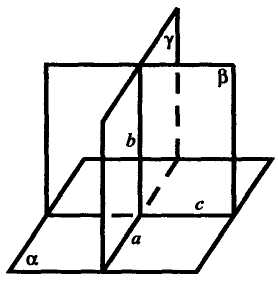Ознака перпендикулярності площин.

Теорема. Якщо пряма проходить через пряму, перпендикулярну до другої площини, то ці площини перпендикулярні

Дано: α — площина, b 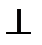α, β проходить через b.

Довести: β 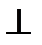α.

Дата добавления: 2015-05-26