КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Доведення
|
|
|
|
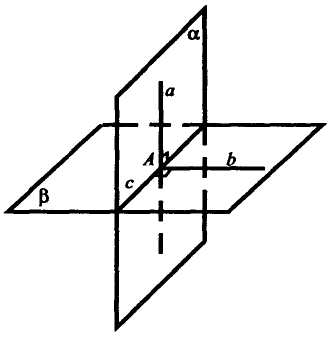 Площини αі β перетинаються по прямій c. У площині αчерез точку перетину b і с проведемо пряму а
Площини αі β перетинаються по прямій c. У площині αчерез точку перетину b і с проведемо пряму а  с. Через прямі а і b проведемо площину γ.
с. Через прямі а і b проведемо площину γ.
γ  с, оскільки с
с, оскільки с 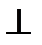 а і с
а і с 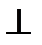 b; пряма а
b; пряма а 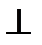 b, тому α
b, тому α 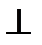 β. Теорему доведено.
β. Теорему доведено.
Властивість: якщо пряма, що лежить в одній з двох перпендикулярних площин, перпендикулярна до лінії їх перетину, то вона перпендикулярна до другої площини.
Дано: α 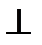 β, α
β, α  β = с, а
β = с, а 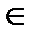 α, а
α, а 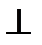 с. Довести: α
с. Довести: α 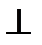 β.
β.
Білет № 10
1. Границя функції в точці. Основні властивості границь.
2. Циліндр. Осьовий переріз циліндра. Переріз циліндра площинами
3. Знайти: 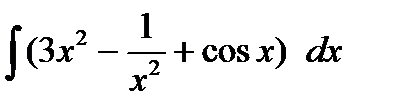 .
.
4. Кінці відрізка А(5; -2; 1 і В(5; 3; 6). Знайти точку, симетричну середині відрізка відносно площини xz.
1. Границя функції в точці. Основні властивості границь.
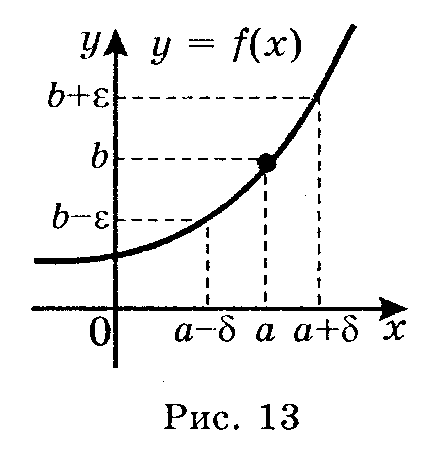
Число b називається границею функції у = f(x) в точці а, якщо для будь-якого ε > 0 існує таке число δ = δ(ε) > 0, що для всіх х: 0 < | х – а | < δ, виконується нерівність | f(x) – b | < ε. (Рис. 15).
Основні властивості границь:
1. Якщо функція f(x) має границю при х → а, то ця границя єдина.
2. Границя постійної функції дорівнює постійній 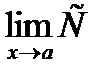 = С, де С — постійна.
= С, де С — постійна.
3. Границя суми (різниці) двох функцій дорівнює сумі (різниці) їхніх границь, при умові, що границі доданків існують.
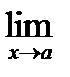 (f(x) ± g(x)) =
(f(x) ± g(x)) = 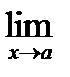 f(х) ±
f(х) ± 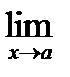 g(x).
g(x).
4. Границя добутку двох функцій дорівнює добутку границь цих функцій, якщо границі множників існують
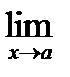 (f(x) · g(x)) =
(f(x) · g(x)) = 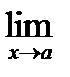 f(x) ·
f(x) · 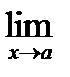 g(x).
g(x).
5. Постійний множник можна виносити за знак границі
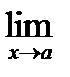 (C f(x)) = С
(C f(x)) = С 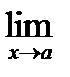 f(x).
f(x).
6. Границя частки двох функцій дорівнює частці границь цих функцій, якщо границі чисельника і знаменника існують і границя знаменника не дорівнює нулю
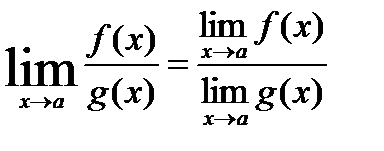 ,
, 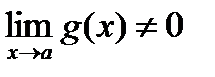 .
.
Приклад, 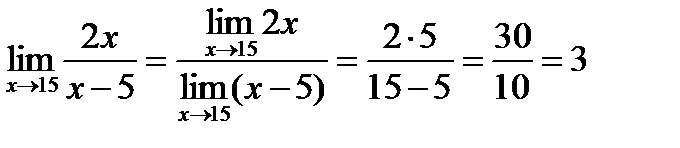
2. Циліндр. Осьовий переріз циліндра. Переріз циліндра площинами
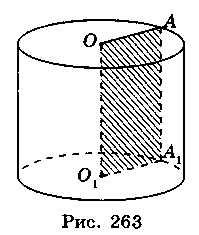
Прямим круговим циліндром називається тіло, утворене обертанням прямокутника навколо його сторони.
На рис. 263 зображено циліндр, утворений обертанням плоского прямокутника ОАВО 1 навколо прямої ОО 1— осі циліндра.
 Сторони ОА і O 1 B описують рівні круги, які лежать у паралельних площинах і називаються основами циліндра. Радіуси кругів називаються радіусами циліндра.
Сторони ОА і O 1 B описують рівні круги, які лежать у паралельних площинах і називаються основами циліндра. Радіуси кругів називаються радіусами циліндра.
Сторона АВ описує поверхню, яка називається бічною поверхнею циліндра. Відрізки бічної поверхні, які паралельні й дорівнюють АВ, називаються твірними циліндра.
Висотою циліндра називається відрізок, перпендикулярний до основ, циліндра, кінці якого належать основам. Висота циліндра дорівнює його твірній.
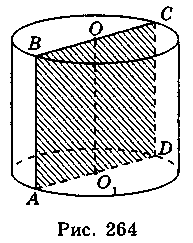
Осьовий переріз циліндра — прямокутник зі сторонами, що дорівнюють висоті циліндра й діаметру його основи. На рис. 264 прямокутник ABCD — осьовий переріз циліндра.
Білет № 11
1. Функція у = sin x, її графік і властивості.
2. Призма. Правильна призма. Площа бічної поверхні прямої призми.
3. Розв’язати нерівність: 3 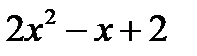 – 5
– 5 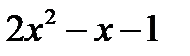 > 5
> 5 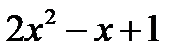 + 3
+ 3 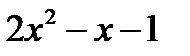
4. У нижній частині циліндра проведено хорду, довжина якої дорівнює b. Цю хорду видно із центра нижньої основи під кутом 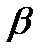 , а відрізок, який сполучає центр верхньої основи із серединою проведеної хорди утворює з площиною основи кут
, а відрізок, який сполучає центр верхньої основи із серединою проведеної хорди утворює з площиною основи кут  . Знайдіть об’єм
. Знайдіть об’єм
1. Функція у = sin x, її графік і властивості
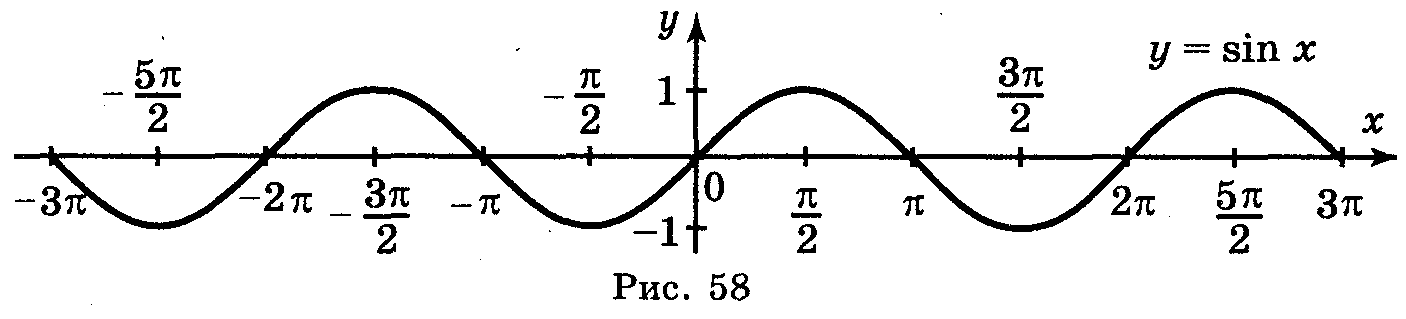 Тригонометричними називають функції, задані формулами:
Тригонометричними називають функції, задані формулами:
y = sinх, y = cos x, y = tg x, y = ctg x.
Крива, яка є графіком функції у = sin x, називається синусоїдою.
Властивості функції y = sin х:
1. Область визначення - проміжок (-∞;+∞).
2. Область значень – проміжок [-1;1].
3. Функція непарна, періодична з періодом Т=2π.
4. Функція зростає при -π/2+2πn < х < π/2+2πn, n є Z.
5. Функція спадає при π/2 + 2πn < х < 3π/2+2πn, n є Z.
6. Функція має максимум у точках (π/2+2πn;0), мінімум у точках (-π/2+2πn;0), nє Z.
2. Призма. Правильна призма. Площа бічної поверхні прямої призми.
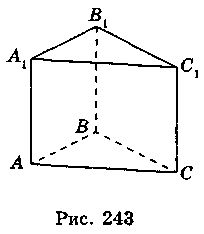 Многогранник, дві грані якого — рівні n -кутники з відповідно паралельними сторонами, а всі інші п граней — паралелограми, називається n-кутною призмою
Многогранник, дві грані якого — рівні n -кутники з відповідно паралельними сторонами, а всі інші п граней — паралелограми, називається n-кутною призмою
Рівні n -кутники призми називаються основами, а паралелограми — бічними гранями, сторони основи — ребрами основи, інші ребра — бічними ребрами.
З означення призми випливає, що основи призми рівні, а також лежать у паралельних площинах. Бічні ребра паралельні й рівні.
Поверхня призми складається з основ і бічної поверхні.
Площею поверхні призми називається сума площ усіх її граней. Оскільки основи рівні, то Snp = S6ічн + 2Sосн,
де Snp — площа поверхні призми;
S6ічн — площа бічної поверхні призми;
Sосн — площа основи.
Призма називається прямою, якщо її бічні ребра перпендикулярні до основи.
Пряма призма називається правильною, якщо в її основі лежить правильний многокутник.
Слід зазначити, що бічними гранями прямої призми є прямокутники.
Площа бічної поверхні прямої призми дорівнює добутку периметра її основи на довжину ребра.
Sбічн = Р ∙ h, де P = a 1 + a 2 +...+ an.
Білет № 12
1. Функція у = cos x, її графік і властивості.
2. Прямокутний паралелепіпед. Центральна симетрія паралелепіпеда.
3. Для заданої функції f (x) = 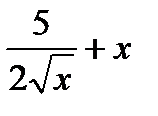 знайдіть первісну, графік якої проходить через точку А (4; -3).
знайдіть первісну, графік якої проходить через точку А (4; -3).
4. Основа піраміди – рівнобедрений трикутник з основою а і кутом α при вершині. Усі двогранні кути при ребрах основи дорівнюють β. Знайдіть об’єм піраміди.
1. Функція у = cos x, її графік і властивості
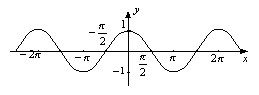
Тригонометричними називають функції, задані формулами:
y = sinх, y = cos x, y = tg x, y = ctg x.
Крива, яка є графіком функції y = cos x, називається косинусоїдою.
Властивості функції y = cos х:
1. Обл. визначення - проміжок (-∞;+∞).
2. Область значень – проміжок [-1;1].
3. Функція парна, періодична з періодом Т=2π.
4. Функція зростає при -π+2πn < х < 2πn, nє Z.
5. Функція спадає при 2πn < х < π+2πn, nє Z.
6. Функція має максимум у точках (2πn;0), мінімум у точках (π+2πn;0), nєZ.
2. Прямокутний паралелепіпед. Центральна симетрія паралелепіпеда.
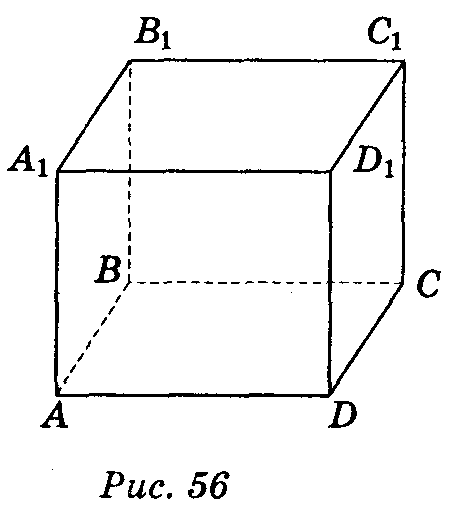 Прямий паралелепіпед, у якого основою є прямокутник, називається прямокутним паралелепіпедом
Прямий паралелепіпед, у якого основою є прямокутник, називається прямокутним паралелепіпедом
Усі грані прямокутного паралелепіпеда — прямокутники.
Усі діагоналі прямокутного паралелепіпеда рівні.
Довжини непаралельних ребер прямокутного паралелепіпеда називають його розмірами (вимірами). У прямокутного паралелепіпеда три лінійні виміри.
Прямокутний паралелепіпед, у якого лінійні виміри рівні, називається кубом.
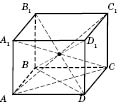 Теорема. Діагоналі паралелепіпеда перетинаються в одній точці й точкою перетину діляться навпіл.
Теорема. Діагоналі паралелепіпеда перетинаються в одній точці й точкою перетину діляться навпіл.
Із цього випливає, що точка перетину діагоналей паралелепіпеда є його центром симетрії.
У прямого паралелепіпеда є чотири діагоналі, які попарно дорівнюють одна одній.
Теорема. У прямокутному паралелепіпеді всі діагоналі рівні. Квадрат діагоналі дорівнює сумі квадратів трьох його вимірів.
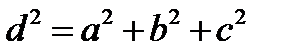
Білет № 13
1. Функція у = tg x, її графік і властивості.
2. Аксіоми стереометрії. Існування площини, що проходить через дану пряму і дану точку.
3. Обчисліть площу фігури, обмеженої лініями у = х2 – 6х + 9, у = 5 – х.
4. Прямокутний трикутник з катетом а і протилежним кутом  обертається навколо прямої, що містить його гіпотенузу. Знайдіть об’єм тіла обертання.
обертається навколо прямої, що містить його гіпотенузу. Знайдіть об’єм тіла обертання.
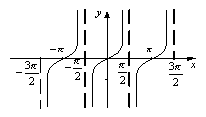
1. Функція у = tg x, її графік і властивості.
Тригонометричними називають функції, задані формулами:
y = sinх, y = cos x, y = tg x, y = ctg x.
Крива, яка є графіком функції y = cos x, називається тангенсоїдою.
Властивості функції y = tgх:
1. Обл. визначення – всі дійсні числа, крім точок (π/2+2πn), n є Z.
2. Область значень – проміжок (-∞;+∞).
3. Функція непарна, періодична з періодом Т = π.
4. Нулі функції – точки (πn;0), n є Z.
5. Функція зростає на всій області визначення.
6. Функція не має екстремумів.
2. Аксіоми стереометрії. Існування площини, що проходить через дану пряму і дану точку.
I. Яка б не була пряма, існують точки, що належать цій прямій, і точки, що не належать їй.
Через будь-які дві точки можна провести пряму, й тільки одну.
II. Із трьох точок на прямій одна й тільки одна лежить між двома іншими.
III. Кожний відрізок має певну довжину, більшу від нуля. Довжина відрізка дорівнює сумі довжин частин, на які він розбивається будь-якою його точкою.
IV. Пряма, що належить площині, розбиває цю площину на дві півплощини.
V. Кожний кут має певну градусну міру, більшу від нуля. Розгорнутий кут дорівнює 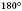 . Градусна міра кута дорівнює сумі градусних мір кутів, на які він розбивається будь-яким променем, що проходить між його сторонами.
. Градусна міра кута дорівнює сумі градусних мір кутів, на які він розбивається будь-яким променем, що проходить між його сторонами.
VI. На будь-якій півпрямій від її початкової точки можна відкласти відрізок даної довжини, й тільки один.
VII. Від півпрямої на площині, що містить її, можна відкласти в задану півплощину кут із даною градусною мірою, меншою за 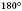 , і тільки один.
, і тільки один.
VIII. Який би не був трикутник, існує трикутник, що дорівнює йому, у даній площині в заданому розміщені відносно даної півпрямої у цій площині.
IX. На площині через дану точку, що не лежить на даній прямій, можна провести не більш як одну пряму, паралельну даній.
До цих аксіом додаються три аксіоми групи С.
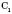 . Яка б не була площина, існують точки, що належать цій площині, і точки, які не належать їй.
. Яка б не була площина, існують точки, що належать цій площині, і точки, які не належать їй.
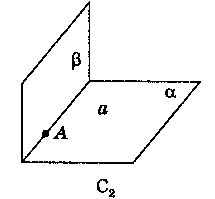
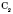 . Якщо дві різні площини мають спільну точку, то вони перетинаються по прямій, що проходить через цю точку.
. Якщо дві різні площини мають спільну точку, то вони перетинаються по прямій, що проходить через цю точку.
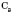 . Якщо дві різні прямі мають спільну точку, то через них можна провести площину, й до того ж тільки одну.
. Якщо дві різні прямі мають спільну точку, то через них можна провести площину, й до того ж тільки одну.
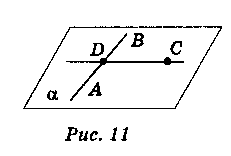
Теорема. Через пряму і точку, яка не лежить на ній, можна провести площину, й до того ж тільки одну.
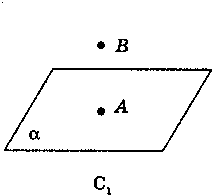
Нехай АВ – данапряма і С – точка, яка їй не належить (рис. 11).
Доведення (існування площини)
| Твердження | Аргумент |
| Візьмемо точку D, яка лежить на прямій АВ | І |
| Через точки D і С проведемо пряму DC | І |
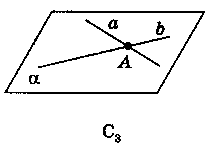
| Через прямі АВ і DC проведемо площину α | С3 |
Доведення (єдиність площини) Доведемо від супротивного. Припустимо, що існує дві площини α і β, які проходять через пряму АВ і, точку С. За аксіомою С2 площини α і β перетинаються по прямій, якій належать А, В, С, що суперечить умові. Отже, площина, яка проходить через пряму і точку, що не належить прямій, єдина.
Білет № 14
1. Залежність між тригонометричними функціями одного і того самого аргументу.
2. Циліндр. Формули об’єму циліндра та площі повної поверхні циліндра.
3. Розв’яжіть рівняння: (х2 – 4х + 3)  = 0.
= 0.
4. З точки А до площини  проведено похилі АВ і АС, які утворюють з площиною кути по 600. Знайдіть відстань між точками В і С, якщо
проведено похилі АВ і АС, які утворюють з площиною кути по 600. Знайдіть відстань між точками В і С, якщо 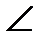 ВАС = 900, а відстань від точки А до площини
ВАС = 900, а відстань від точки А до площини  дорівнює 3 см.
дорівнює 3 см.
1. Залежність між тригонометричними функціями одного і того самого аргументу.
| у |
| х |
| y |
| x |
| М(х; у) |
| N |
| α |
| О |
Згадаємо: y= sin a; x=cos a.
За теоремою Піфагора: y2+x2=12 або
| sin2a + cos2a=12. | (1) |
За означенням:
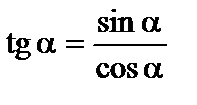 ; ;
| (2) |
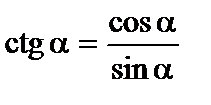
| (3) |
| tg a × ctg a=1; | (4) |
Скористаємося рівністю (1). Почленно поділимо на sin2a. Одержимо:
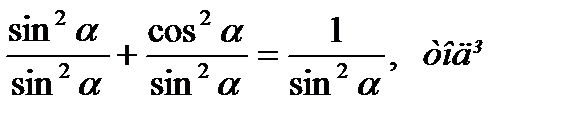
| 1+ctg2a= 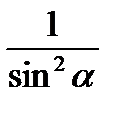 . .
| (7) |
Почленно поділимо на cos2a. Одержимо:
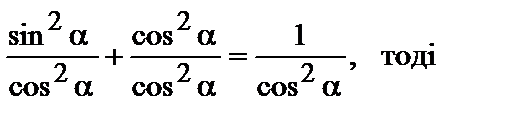
| 1+tg2a= 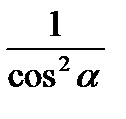 . .
| (8) |
2. Циліндр. Формули об’єму циліндра та площі повної поверхні циліндра

Прямим круговим циліндром називається тіло, утворене обертанням прямокутника навколо його сторони.
На рис. 263 зображено циліндр, утворений обертанням плоского прямокутника ОАВО 1 навколо прямої ОО 1— осі циліндра.
Сторони ОА і O 1 B описують рівні круги, які лежать у паралельних площинах і називаються основами циліндра.
Радіуси кругів називаються радіусами циліндра.
Сторона АВ описує поверхню, яка називається бічною поверхнею циліндра. Відрізки бічної поверхні, які паралельні й дорівнюють АВ, називаються твірними циліндра.
Висотою циліндра називається відрізок, перпендикулярний до основ, циліндра, кінці якого належать основам. Висота циліндра дорівнює його твірній.
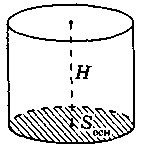
Об'єм циліндра дорівнює добутку площі його основи на висоту
V = S осн ∙ H; V = πR 2 H
Білет № 15
1. Тригонометричні функції подвійного аргументу
2. Декартові координати у просторі. Відстань між точками у просторі.
3. Розв’яжіть рівняння: log 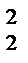 (4x) + log2
(4x) + log2 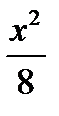 = 8
= 8
4. Діагональ прямокутного паралелепіпеда дорівнює d і утворює з площиною основи кут α, а з площиною бічної грані – кут β. Знайдіть площу бічної поверхні паралелепіпеда.
1. Тригонометричні функції подвійного аргументу
| Примітка: Інколи при перетворенні тригонометричних виразів користуються формулами: універсальна підстановка | |
|
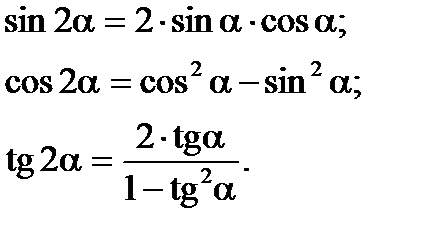
|
2. Декартові координати у просторі. Відстань між точками у просторі
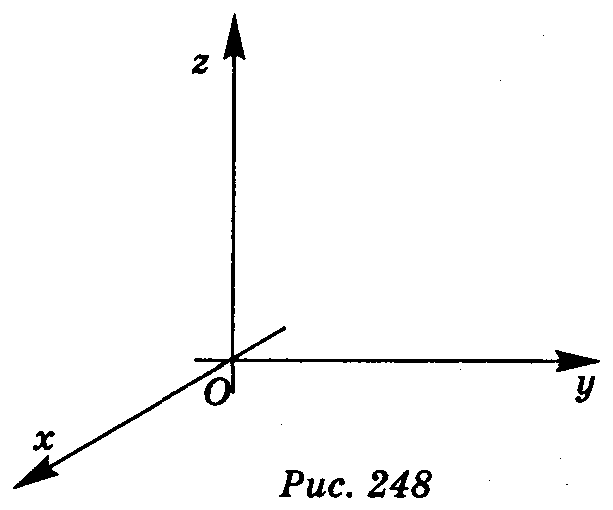 Нехай х, у, z — три попарно перпендикулярні координатні прямі, які перетинаються в точці О (рис. 248). Ці координатні прямі називаються координатними осями: вісь х, вісь у, вісь z або вісь абсцис, вісь ординат, вісь аплікат відповідно, точку О називають початком координат.
Нехай х, у, z — три попарно перпендикулярні координатні прямі, які перетинаються в точці О (рис. 248). Ці координатні прямі називаються координатними осями: вісь х, вісь у, вісь z або вісь абсцис, вісь ординат, вісь аплікат відповідно, точку О називають початком координат.
Кожна вісь точкою О розбивається на дві півосі — додатну, позначену стрілкою, і від'ємну.
Площини, які проходять через х і у, х і z, у і z, називають координатними площинами і позначають відповідно: ху, хz, уz.
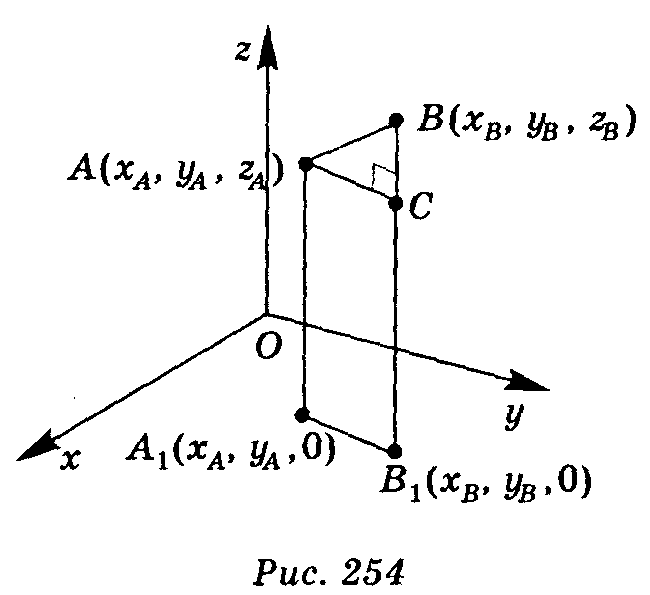 Твердження. Квадрат, відстані між двома точками дорівнює сумі квадратів різниць їх відповідних координат.
Твердження. Квадрат, відстані між двома точками дорівнює сумі квадратів різниць їх відповідних координат.
|
|
|
|
|
Дата добавления: 2015-05-26; Просмотров: 3031; Нарушение авторских прав?; Мы поможем в написании вашей работы!