Доведення

Нехай F(x) і F₁(x) — дві первісні однієї і тієї самої функції f(x), тобто F'(x) = f(x), F₁'(x) = f(x). Похідна різниці g(x) = F(x) – F₁(x) дорівнює нулю, оскільки g'(x) = F₁'(x) - F'(x) = = f(x) - f(x) = 0. Якщо g'(x) = 0 на деякому проміжку, то дотична до графіка функції у = g(x) у кожній точці цього проміжку паралельна осі ОХ. Тому графіком функції у = g(x) є пряма, яка паралельна осі ОХ, тобто g(x) = С, де С — деяка стала. Із рівностей g(x) = С,

g(x) = F₁(x) - F(x) випливає, що F₁(x) – F(x) = С, або F₁(x) = F(x) + С.

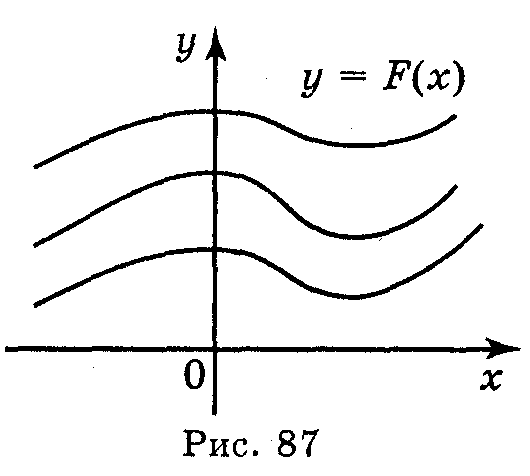
Основній властивості первісної можна надати геометричного змісту: графіки будь-яких двох первісних для функції f одержуються один із одного паралельним перенесенням вздовж осі ΟΥ (рис. 87).

2. Пряма і правильна призми. Площі бічної та повної поверхні призми.

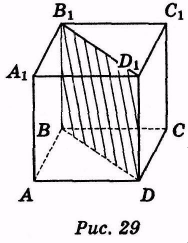
Призма називається прямою, якщо її бічні ребра перпендикуляр­ні до основи. Інші призми називаються похилими.

Пряма призма називається правильною, якщо в її основі лежить правильний многокутник.

Площею бічної поверхні (бічною поверхнею) призми називаєть­ся сума площ бічних граней.

Повна поверхня призми дорівнює сумі бічної поверхні і площ основ:

S_пр = S_біч + 2S_осн

Висотою призми називається відстань між площинами її основ. Відрізок, який сполучає дві вершини призми, що не належать одній і рані, називається діагоналлю призми.

Білет № 27

1. Первісна. Правила знаходження первісних.

2. Циліндр. Осьовий переріз циліндра. Формули об’єму та повної поверхні циліндра

3. Довести тотожність .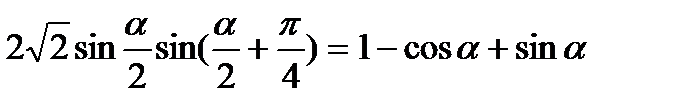

4. Основа піраміди – ромб із стороною а і кутом α. Усі двогранні кути при ребрах основи дорівнюють β. Знайдіть об’єм піраміди.

1. Первісна. Правила знаходження первісних.

Функція F(x) називається первісною функції f(x) на деякому про­міжку, якщо для всіх x із цього проміжку виконується рівність: F'(х) = f(x).

Загальний вигляд первісних для функції f(x) на проміжку [ a;b ] є F(x) + С, де C – довільна стала, а F(x) – одна з первісних для f(x) на проміжку [ a;b ].

Правила знаходження первісних:

1.Якщо F(x) і G(x) — первісні відповідно функцій f(x) і g(x) на деякому проміжку, то функція F(x) ± G(x) є первісною функції f(x) ± g(x).

2. Якщо F(x) є первісною для функції f(x), a C — ста­ла, то CF(x) — первісна для функції Cf(x).

3. Якщо F(x) є первісною для f(x), a k і b — постійні числа, причому k 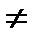0, то 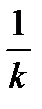F(kx +b) є первісною для функції f(kx + b).

2. Циліндр. Осьовий переріз циліндра. Формули об’єму та повної поверхні циліндра

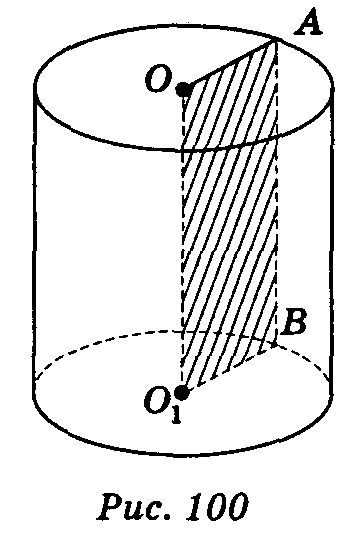
Прямим круговим циліндром називається тіло, утворене обертанням прямокутника навколо його сторони. Сторони ОА і 0₁В описують рівні круги, які лежать у паралель­них площинах і називаються основами циліндра. Радіуси кругів на­зиваються радіусами циліндра. Сторона АВ описує поверхню, яка називається бічною поверхнею циліндра. Відрізки бічної поверхні, які паралельні і дорівнюють АВ, називаються твірними циліндра.

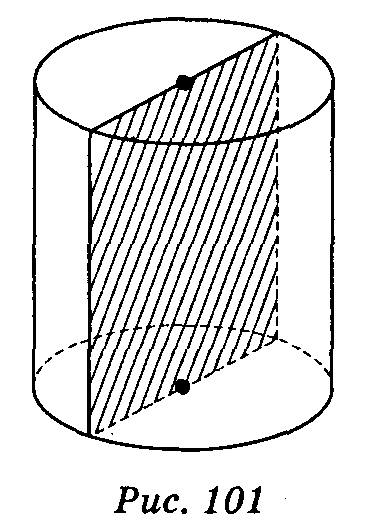Висотою циліндра називається відрізок, перпендикулярний до основ циліндра, кінці якого належать основам. Висота циліндра до­рівнює його твірній.

Осьовий переріз циліндра — прямокутник зі сторонами, що до­рівнюють висоті циліндра і діаметру його основи

Площа бічної поверхні циліндра обчислюється за формулою: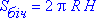

де R – радіус, а H – висота циліндра.

Об'єм циліндра дорівнює добутку площі його основи на висоту:

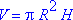
Білет № 28

1. Загальна схема дослідження функції за допомогою похідної.

2. Ознака колінеарності векторів.

3. Розв’яжіть рівняння: sin 2x + cos 2x = 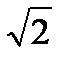sin 3x.

4. З точки А до площини проведено похилі АВ і АС, довжини яких 15 см і 20 см відповідно. Знайдіть відстань від точки А до площини, якщо проекції похилих на цю площину відносяться як 9: 16.

1. Загальна схема дослідження функції за допомогою похідної

Дослідження функції і побудову її графіка будемо виконува­ти за таким планом:

1. Знаходимо область визначення функції.

2. Знаходимо точки перетину графіка з координатними осями.

3. З'ясовуємо парність (непарність), періодичність функції.

4. Знаходимо похідну та стаціонарні точки.

5. Знаходимо проміжки зростання, спадання, точки екстремуму та екстремальні значення функції.

6. З'ясовуємо поведінку функції на кінцях області визначення.

7. На підставі проведеного дослідження будуємо графік функції

2. Ознака колінеарності векторів

Вектором називають напрямлений відрізок.

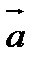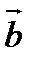Вектор, у якого початок збігається з кінцем, називається нульовим вектором. Ненульові вектори називаються колінеарними, якщо вони ле­жать або на одній прямій, або на паралельних прямих. Ненульові вектори і називаються однаково напрямлени­ми, якщо вони колінеарні та напрямлені в один бік.

Ознака колінеарності векторів

Якщо вектори колінеарні, то їхні відповідні координати про­порційні. І навпаки, якщо відповідні координати двох векторів пропорційні, то ці вектори колінеарні.

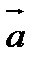
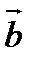
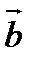
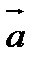
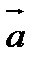
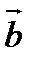
ll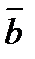

Білет № 29

1. Визначений інтеграл, його геометричний зміст та властивості.

2. Паралельне проектування та його властивості. Ортогональне проектування.

3. Обчисліть площу фігури, обмеженої лініями: у = 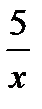, у = 4х + 1, х = 2.

4. У правильній трикутній призмі АВСА₁В₁С₁ сторона основи дорівнює 8 см, а бічне ребро – 2 см. Через сторону АС нижньої основи і середину сторони А₁В₁ верхньої проведено площину. Знайдіть площу перерізу.

1. Визначений інтеграл, його геометричний зміст та властивості

Визначений інтеграл записується у вигляді формули Ньютона-Лейбніца

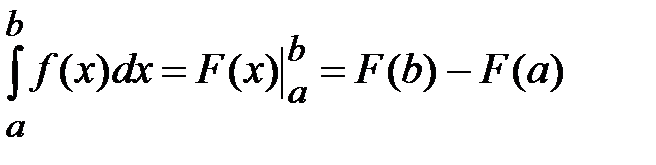
де 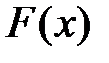- первісна функції 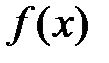або невизначений інтеграл.

Властивості визначеного інтеграла:

Визначений інтеграл має ті ж властивості, що й невизначений. Крім того:

1^о. Якщо відрізок інтегрування [ a, b ] розбитий на дві частини [ a, с ] і [ с, b ], то

.

2^о. .

3^о. 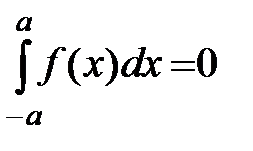, якщо .

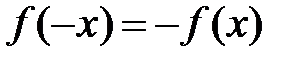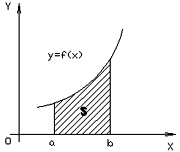4^о. 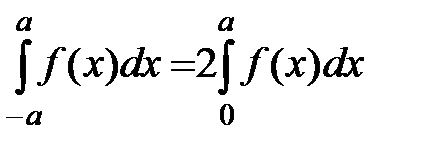, якщо .

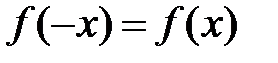Геометричний зміст визначеного інтеграла:

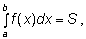
де S - площа фігури, обмеженої графіком функції y = f(x) і прямими х = а, х = b і y = 0.

Криволінійною трапецією називається фігура, обмежена графі­ком неперервної функції у = f(x), яка не змінює знак на відрізку [ а; b ], прямими x = а, х = b і відрізком [ а; b ]

2. Паралельне проектування та його властивості. Ортогональне проектування.

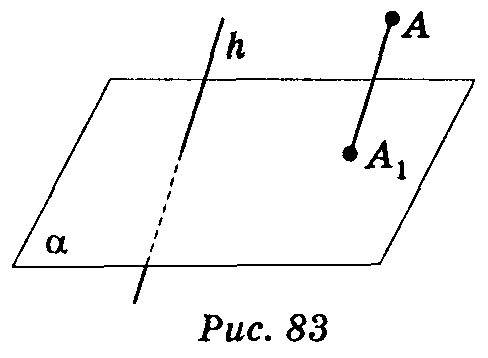Нехай дано довільну площину α, точку А (рис. 83) і пряму h, яке перетинає площину α. Проведемо через точку А пряму, яка паралель­на h, вона перетинає площину α у деякій точці А₁. Знайдену таким способом точку А; називають паралельною проекцією точки А на площину α у напря­мі h. Пряму h називають проектуючою пря­мою, площину α — площиною проекцій.

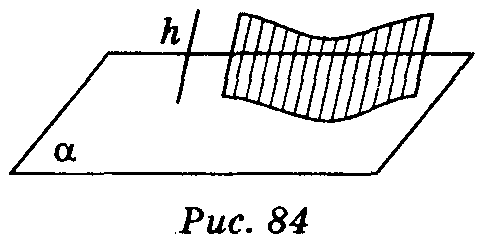Щоб побудувати проекцію будь-якої фігу­ри, треба спроектувати на площину проекції кожну точку даної фігури (рис. 84). Наведемо деякі властивості паралельного проектування.

Теорема. Якщо відрізки, які проектуються, не паралельні проектуючій прямій, то при паралельному проектуванні:

1) відрізки зображаються відрізками;

2) паралельні відрізки зображаються паралельними відрізками або відрізками однієї прямої;

3) відношення довжин паралельних відрізків і відрізків однієї прямої зберігається.

Якщо проектуючі прямі перпендикулярні до площини проекцій, таке проектування називають ортогональним, або прямокутним. Ортого­нальне проектування — вид паралельного проектування, тому воно має властивості паралельного проектування.

Білет № 30

1. Екстремуми функції. Дослідження функцій на екстремум.

2. Основні поняття теорії ймовірностей. Класичне означення ймовірностей

3. Розв’яжіть рівняння: .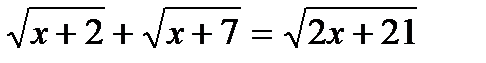

4. У правильній трикутній піраміді плоский кут при вершині дорівнює . Знайдіть об’єм піраміди, якщо її висота дорівнює h.

1. Екстремуми функції. Дослідження функцій на екстремум.

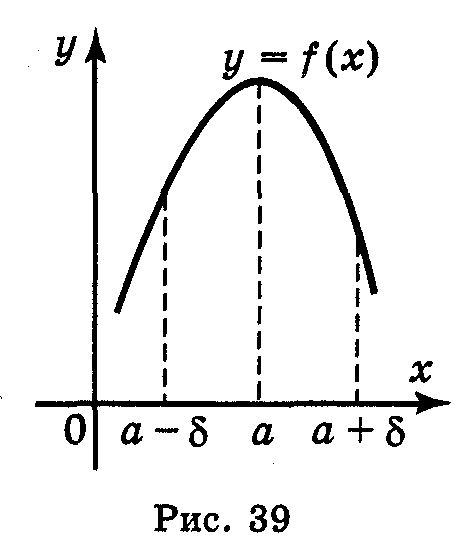Означення. Точка а із області визначення функції f(x) називаєть­ся точкою максимуму цієї функції, якщо існує та­кий окіл точки а, що для всіх х 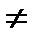а із цього околу виконується нерівність f(x) < f(a). (Рис. 39)

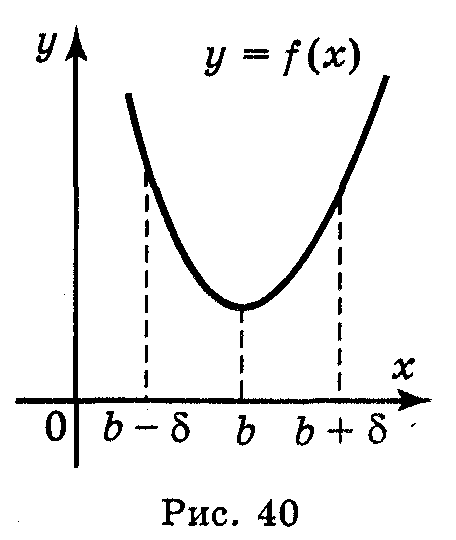
Означення. Точка b із області визначення функції f(x) називаєть­ся точкою мінімуму цієї функції, якщо існує такий окіл точки b, що для всіх х 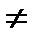b із цього околу вико­нується нерівність f(x) < f(b). (Рис. 40).

Точки максимуму і точки мінімуму називають точ­ками екстремуму функції, а значення функції в цих точках називають екстремумами функції (максимум і мінімум функції).

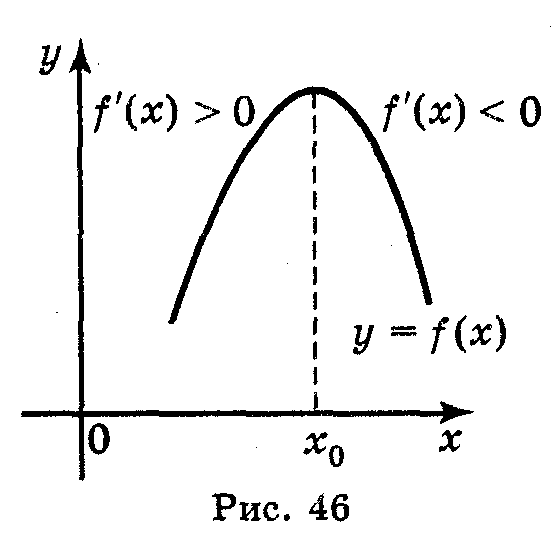Точки максимуму позначають х_max, а точки мінімуму — х_min. Значення функції в цих точках, тобто максимуми і мінімуми функції, позначаються відповідно: у_max і у_min.

Якщо похідна ліворуч стаціонарної точки додатна, а праворуч — від'ємна, тобто при переході через цю точку по­хідна змінює знак з «+» на «–», то ця стаціонарна точка є точкою максимуму (рис. 46)

Дослідження функцій на екстремум:

1. Знайти область визначення функції.

2. Знайти похідну функції f`(x)

3. Знайти стаціонарні точки: f(x) = 0

4. Наносимо область визначення та стаціонарні точки на коор­динатну пряму і визна­чимо знак похідної на кожному проміжку

5. Вказати точки екстремуму

2. Основні поняття теорії ймовірностей. Класичне означення ймовірностей

Подія — це явище, про яке можна сказати, що воно відбу­вається чи не відбувається за певних умов. Події позначаються великими буквами латинського алфавіту: А, В, С... Будь-яка подія відбувається внаслідок випробування (експерименту, досліду).

Випробування — це умови, в результаті яких відбувається (чи не відбувається) подія.

Випадкова подія — подія, яка може або відбутися, або не відбутися (за певних обставин) при багаторазовому випробуванні.

Якщо подія обов'язково відбудеться при багаторазовому випробуванні, то вона називається вірогідною.

Приклади: а) після четверга наступає п'ятниця; б) сонце сходить на сході.

Якщо подія не відбудеться при багаторазовому випробуванні, то вона називається неможливою.

Приклад: а) після зими настає літо; б) з ящика, у якому є тільки білі кульки, витягують чорну кульку.

Ймовірність (випадкової події) — це число, яке показує відношення числа випробувань, у яких дана подія відбулась, до числа всіх випробувань.

Класичне означення ймовірності: Р(А) = 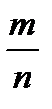— формула обчислення ймовірності, де Р(А) — ймовірність події А; т — кількість сприятливих випробувань (коли подія А настала); п — кількість усіх випробувань.

Властивості ймовірності будь-якої події

1. 0 ≤ Р(А) ≤ 1.

2. Якщо А — вірогідна подія, то Р(А) = 1.

3. Якщо А — неможлива подія, то Р(А) = 0.

4. Якщо А — випадкова подія, то 0 < Р(А) < 1.

Дата добавления: 2015-05-26