Теорема про три перпендикуляри

Теорема 1.(пряма теорема) Якщо пряма, проведена на площині через основу похилої, перпендикулярна до її проекції, то вона перпендикулярна до похилої (див. рисунок).

Теорема 2.(обернена теорема) Якщо пряма на площині перпендикулярна до похилої, то вона перпендикулярна і до проекції похилої.

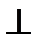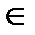Теорема 1.(пряма теорема) Дано:АВ α; С 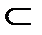α, с α; с 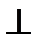ВС (рис. 194)

Довести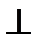: c AC

Доведення. Через точку С і пряму АВ проводимо β і в ній А₁С: А₁С || АВ. Оскільки А₁С || АВ і АВ 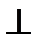α, то А₁С 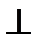α, А₁С 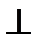с. Оскільки 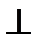с ВС, с 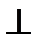А₁С, то с 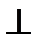β, отже, с 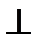AC.

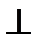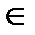Теорема 2.(обернена теорема) Дано:АВ α; С 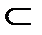α, с α; с 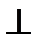АС (рис. 194).

Довести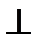: c BC.

Доведення. Через точку С і пряму АВ проводимо β і в ній А₁С: А₁С || АВ. Оскіль­ки А₁С || АВ і АВ 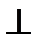α, то A₁С 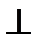α, А₁С 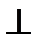с. Оскільки АС 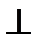с, А₁С 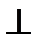с, то β і с, отже, BC 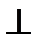с.

Білет № 25

1. Геометричний зміст похідної. Рівняння дотичної до графіка функції.

2. Паралелепіпед та його властивості.

3. Знайдіть область визначення функції: f (x) = lg (6x – x²) + .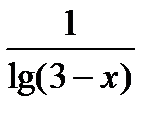

4. У кулі на відстані 12 см від її центра проведено переріз, площа якого дорівнює 64 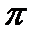см². Знайдіть площу поверхні кулі.

1. Геометричний зміст похідної. Рівняння дотичної до графіка функції.

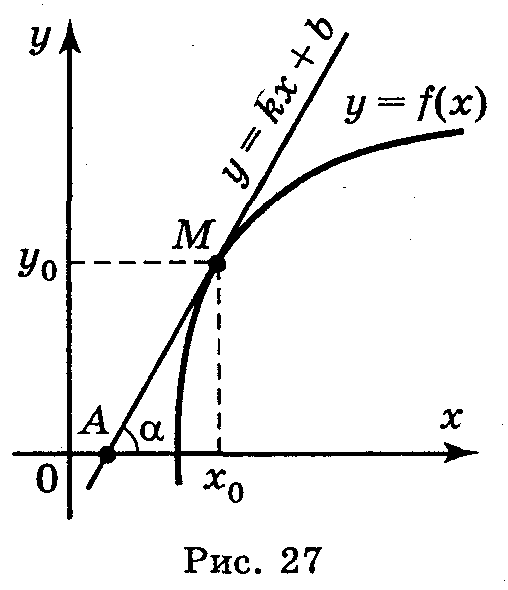
Геометричний зміст похідної: значення похідної функції y = f(x) у точці x₀ дорівнює кутовому коефіцієнту дотичної до графіка функції в точці з абсцисою x₀:
y' = f'(x₀) = k = tgα.

Дотичною до графіка функціїF(x) у точці з абсцисою х₀ називається граничне положення січної до графіка даної функції, що проходить через дві точки графіка, одна з яких має абсцису х₀, якщо різниця абсцис цих точок прямує до нуля.

Рівняння дотичної до кривої у = f(x) в точці М(x_o; у_o) має вигляд:

y – y_о = f '(x_o)(x – x_o).

Рівняння дотичної до кривої у = f(x) у заданій точці x_o можна знаходити за таким планом (схемою):

1. Записуємо рівняння (2) дотичної: y – y_о = f '(x_o)(x – x_o).

2. Знаходимо у_o = f(x_o)·

3. Знаходимо значення f '(x) у точці x_o: f '(x_o).

4. Підставляємо значення x_o, y_o і f '(x_o) y рівняння (2).

2. Паралелепіпед та його властивості.

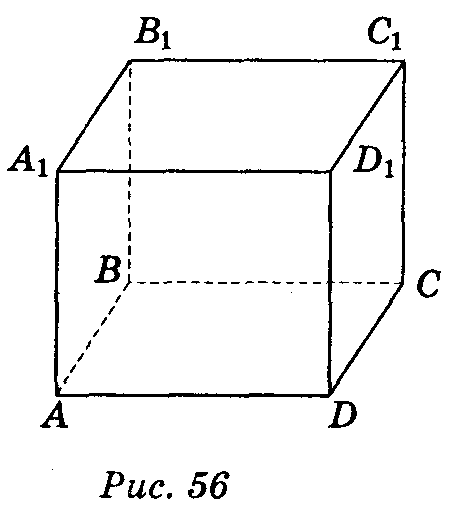Паралелепіпедом називається призма в основі якої лежить паралелограм.

Розрізняється декілька типів паралелепіпедів:

• Прямокутний паралелепіпед - це паралелепіпед, у якого всі грані прямокутники;
• Прямий паралелепіпед - це паралелепіпед, у якого 4 бічні грані прямокутники;
• Похилий паралелепіпед - це паралелепіпед, бічні грані якого не перпендикулярні підставах.

· Куб - це прямокутний паралелепіпед з рівними вимірами. Всі шість граней куба - рівні квадрати.

Властивості:

♦ Протилежні грані паралелепіпеда паралельні та рівні.

♦ Діагоналі паралелепіпеда перетинаються в одній точці і точкою перетину діляться пополам

♦ Точка перетину паралелепіпеда є його центром симетрії.

♦ Паралелепіпед в основі якого лежить прямокутник називається прямим.

♦ У прямокутному паралелепіпеді квадрат будь-якої діагоналі дорівнює сумі квадратів трьох його вимірів

Білет № 26

1. Первісна. Основна властивість первісної.

2. Пряма і правильна призми. Площі бічної та повної поверхні призми.

3. Розв’яжіть рівняння: 27 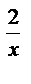+ 2 3 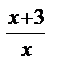– 27 = 0.

4. Через вершину прямого кута С трикутника АВС до площини трикутника проведено перпендикуляр КС, довжина якого дорівнює 4 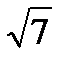см. Знайдіть відстань від точки К до прямої АВ, якщо АС = ВС = 8 см.

1. Первісна. Основна властивість первісної.

Функція F(x) називається первісною функції f(x) на деякому про­міжку, якщо для всіх x із цього проміжку виконується рівність: F'(X) = f(x).

Теореми 1 і 2 виражають основну властивість первісної

Теорема 1. Нехай функція F(x) є первісною для f(х) на деякому проміжку. Тоді для довільної постійної С функція F(x) + С також є первісною для функції f(х).

Доведення

Оскільки F(x) — первісна функції f(x), то F'(x) = f(x). Тоді (F(x) + С) ' = F'(x) + С' = f(х) + 0 = f(x), а ця рівність озна­чає, що F(x) + С є первісною для функції f(х).

Теорема 2. Нехай функція F(x) є первісною для f(x) на деякому проміжку. Тоді будь-яка первісна для функції f(x) на цьому проміжку може бути записана у вигляді F(x) + С, де С — деяка стала (число).

Дата добавления: 2015-05-26