
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Доведення. Нехай дано дві точки А(xA, уA, zA) і В(хB, yB, zB) (рис
|
|
|
|
Нехай дано дві точки А(x A, у A, z A) і В(х B, y B, zB) (рис. 254). Доведемо, що
АВ2 = (х B – x A)2 + (y B – у A)2 + (zB – z A)2.
Розглянемо випадок, коли АВ не паралельна осі z. Через точки А і В проведемо прямі, паралельні осі z. Вони перетнуть площину ху в точках A1 і В1 відповідно. Ці точки мають ті самі координати х, у, що й точки А і В, а координата z їх однакова і дорівнює нулю. Проведемо через точку А площину, паралельну координатній площині ху. Побудована площина перетне пряму ВВ1 у деякій точці С, причому ВС = | zB – z A|. За теоремою Піфагора із ΔАВС маємо:
АВ2 = AC2 + ВС2. Оскільки АС2 = A1В12 = (х B – x A)2 + (y B – у A)2,
ВС = | zB – z A |, то АВ2 = (х B – x A)2 + (y B – у A)2 + (zB – z A)2.
Таким чином, відстань між точками А(x A, у A, z A) і В(х B, y B, zB) обчислюється за формулою 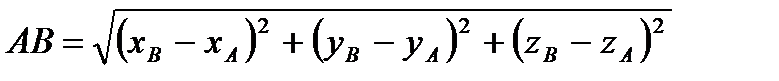 .
.
Білет № 16
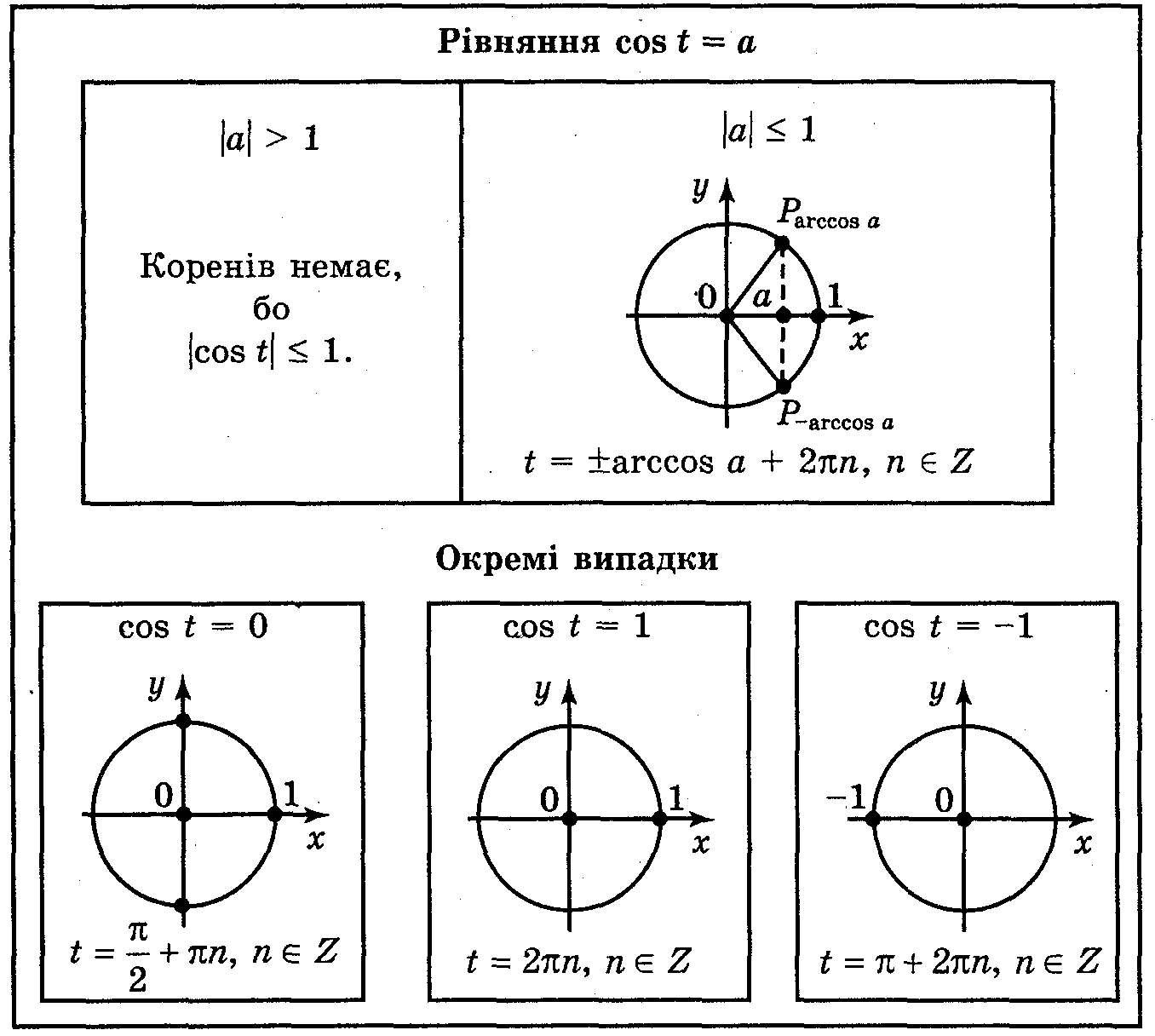
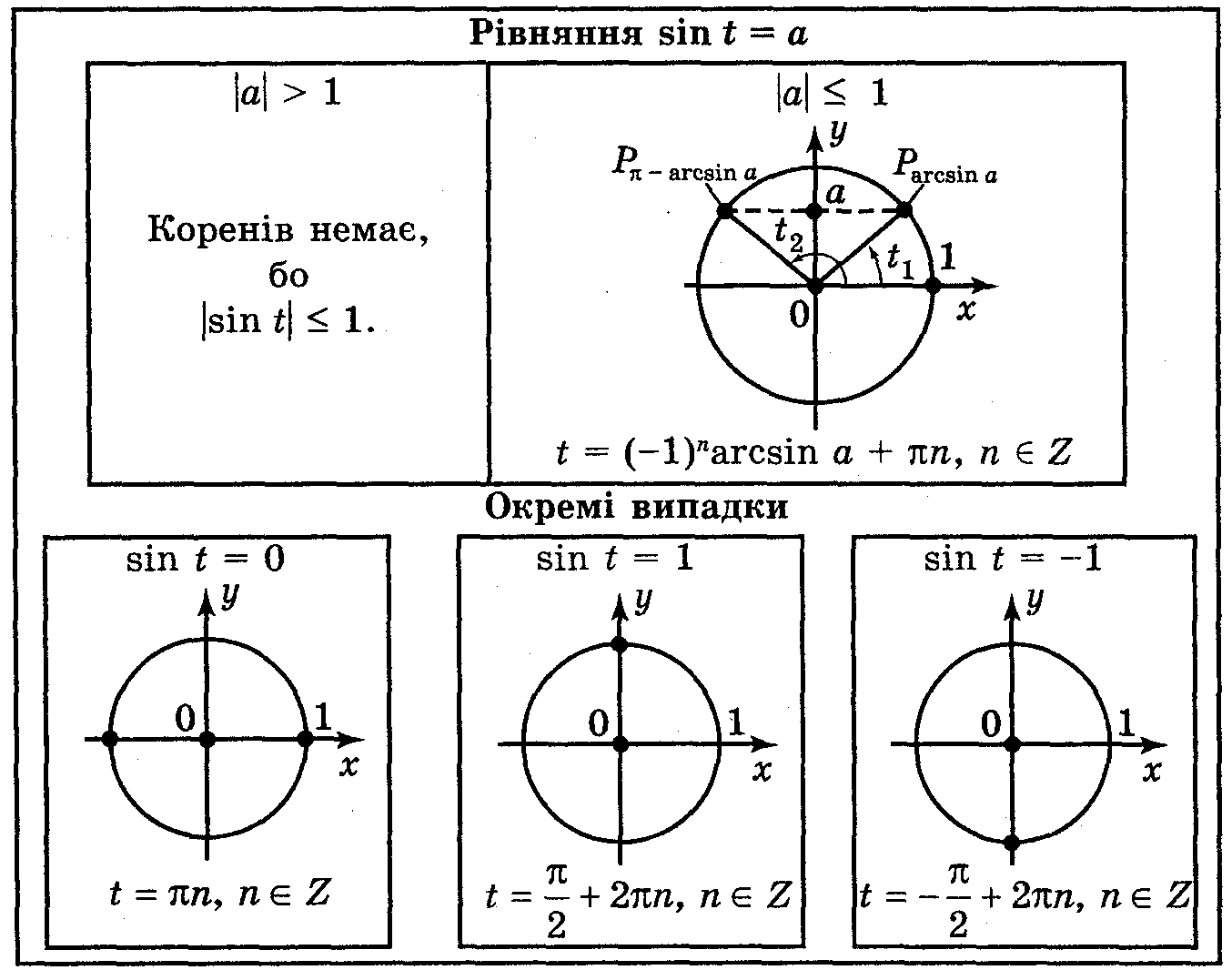
1. Тригонометричні рівняння. Розв’язування рівнянь виду: sin x = a, cos x = a.
2. Правильна піраміда, Площа бічної поверхні правильної піраміди.
3. Знайти проміжки, на яких функція f(x) = x3 – x2 – 5x – 3 зростає, спадає
4. Основа піраміди – квадрат зі стороною 12 см, а дві суміжні бічні грані перпендикулярні до площини основи. Обчисліть площу бічної поверхні піраміди, якщо її висота дорівнює 5 см.
1. Тригонометричні рівняння. Розв’язування рівнянь виду: sin x = a, cos x = a.
Рівняння називаються тригонометричними, якщо змінна величина знаходиться під знаком тригонометричної функції. Найпростішими тригонометричними рівняннями називаються рівняння виду:
sin x=a; cos x=a; tg x=a; ctg x=a.
2. Правильна піраміда, Площа бічної поверхні правильної піраміди.
Правильною пірамідою називається піраміда, в основі якої лежить правильний многокутник, а основа висоти піраміди збігається з центром цього многокутника.
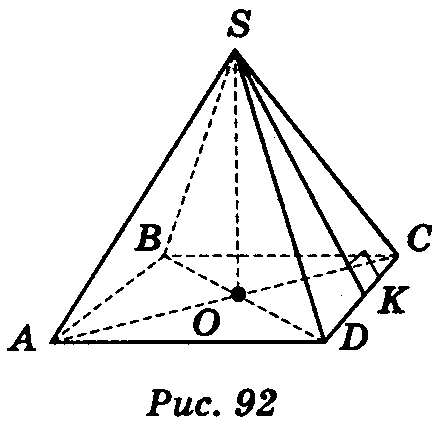
Нехай S АВСD — правильна чотирикутна піраміда (рис. 92). Тоді за означенням її основа АВСD — правильний чотирикутник (квадрат); центр квадрата точка О — основа висоти S0 піраміди.
Пряма, яка містить висоту піраміди, називається віссю правильної піраміди. Висота бічної грані правильної піраміди, яка проведена з вершини піраміди, називається апофемою. На рис. 92 S К — апофема.
У правильної піраміди:
1) бічні ребра рівні;
2) бічні грані рівні;
3) апофеми рівні;
4) двогранні кути при основі рівні;
5) двогранні кути при бічних ребрах рівні;
6) кожна точка висоти правильної піраміди рівновіддалена від всіх вершин основи;
7) кожна точка висоти правильної піраміди рівновіддалена від усіх бічних граней.
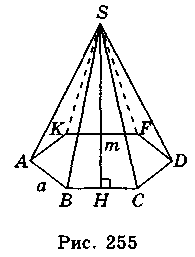
Теорема. Площа бічної поверхні правильної піраміди дорівнює добутку півпериметра її основи на апофему.
Доведення
Нехай а — сторона основи правильної п -кутної піраміди (рис. 255). SH 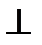 BC, SH = m.
BC, SH = m.
Тоді площа бічної грані правильної піраміди дорівнює 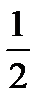 am, а площа бічної поверхні Sбічн =
am, а площа бічної поверхні Sбічн = 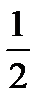 атп. Оскільки
атп. Оскільки 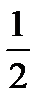 ап = р, де р — півпериметр основи піраміди, то S бічн = pm.
ап = р, де р — півпериметр основи піраміди, то S бічн = pm.
Білет № 17
1. Тригонометричні рівняння. Розв’язування рівнянь виду: tg x = a, ctg x = a.
2. Конус. Формули об’єму конуса та площі повної поверхні конуса.
3. Дослідіть функцію f (x) = x4 –4x2 та побудуйте її графік.
4. Через дві твірні конуса, кут між якими дорівнює α, проведено переріз, який утворює з площиною основи конуса кут β. Знайдіть площу бічної поверхні конуса, якщо його висота рівна Н.
1. Тригонометричні рівняння. Розв’язування рівнянь виду: tg x = a, ctg x = a.
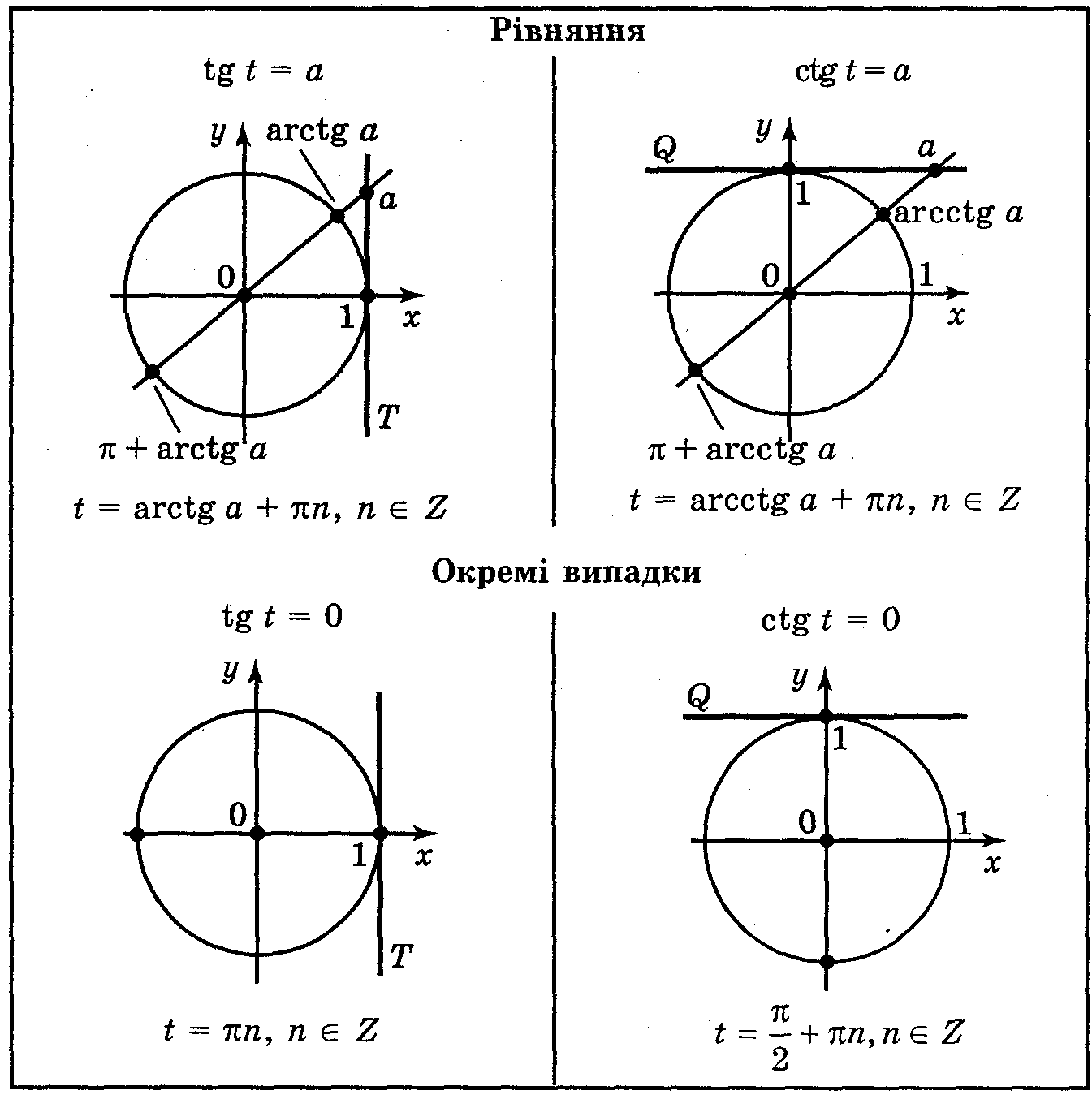
Рівняння називаються тригонометричними, якщо змінна величина знаходиться під знаком тригонометричної функції.
Найпростішими тригонометричними рівняннями називаються рівняння виду:
sin x=a; cos x=a; tg x=a; ctg x=a.
2. Конус. Формули об’єму конуса та площі повної поверхні конуса.
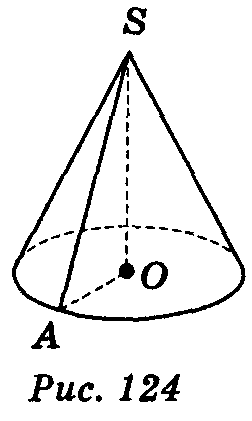
Прямим круговим конусом називається тіло, утворене обертанням плоского прямокутного трикутника навколо одного із його катетів.
Якщо прямокутний трикутник SАО обертається навколо катета SO, то його гіпотенуза описує бічну поверхню, а катет ОА — круг — основу конуса. Радіус цього круга називається радіусом конуса; точка S, відрізок SА, відрізок SO, пряма SO називаються відповідно вершиною, твірною, висотою і віссю конуса.
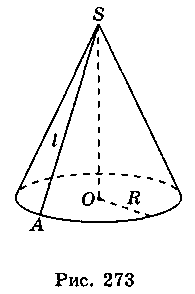
 Площа поверхні та об'єм конуса
Площа поверхні та об'єм конуса
Бічну поверхню конуса можна розгорнути на площину, розрізавши її по твірній (рис. 273).
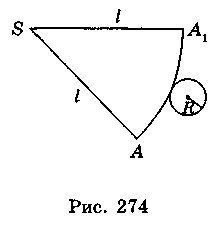
Розгорткою бічної поверхні конуса є круговий сектор, радіус якого дорівнює твірній конуса, а довжина дуги сектора — довжині кола основи конуса (рис. 274).
Площею бічної поверхні конуса будемо вважати площу її розгортки.
Таким чином, площа бічної поверхні конуса дорівнює добутку половини довжини кола основи на твірну: Sбічн = πRl.
Площею повної поверхні конуса називається сума площ бічної поверхні та основи. Для обчислення площі повної поверхні конуса Sкон одержуємо:
Sкон = Sбічн + Sосн, S кон = πRl + πR 2 = π R (l + R).
Об'єм конуса дорівнює третині добутку площі його основи на висоту:
V = 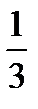 π R 2 H.
π R 2 H.
Білет № 18
1. Корінь п –го степеня і його властивості.
2. Взаємне розміщення прямої і площини в просторі. Ознака паралельності прямої і площини.
3. Знайдіть похідну функції f (x) = log4 (x2 – 4x) та обчисліть її значення в точці х0 = 5.
4. Паралельно осі циліндра проведено переріз, який відтинає від кола основи дугу, градусна міра якої дорівнює 1200. Площа перерізу дорівнює 16 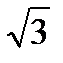 см2, а його діагональ утворює з площиною основи кут 600. Знайдіть площу бічної поверхні циліндра.
см2, а його діагональ утворює з площиною основи кут 600. Знайдіть площу бічної поверхні циліндра.
1. Корінь п –го степеня і його властивості.
Коренем п-го степеня із дійсного числа а називається число, n -й степінь якого дорівнює а.
Згідно даного означення, корінь п -го степеня — це корінь рівняння хn = а. Число коренів цього рівняння залежить від п і а.
Якщо п — парне, тобто п = 2k, k 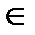 N, то рівняння х 2k = а має два корені, якщо а > 0; один корінь, якщо а = 0; не має коренів, якщо а < 0.
N, то рівняння х 2k = а має два корені, якщо а > 0; один корінь, якщо а = 0; не має коренів, якщо а < 0.
Якщо п — непарне, тобто п = 2k + 1, k 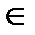 N, то рівняння х2k+1 = а завжди має лише один корінь.
N, то рівняння х2k+1 = а завжди має лише один корінь.
Арифметичним коренем n-го степеня із невід'ємного числа а називається таке невід'ємне число, n -й степінь якого дорівнює а.
Арифметичний корінь п -го степеня із числа а позначають так: 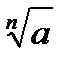 . Число n називають показником кореня, число а — підкореневим числом (виразом).
. Число n називають показником кореня, число а — підкореневим числом (виразом).
Якщо п = 2, то замість 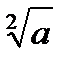 пишуть
пишуть 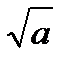 і називають арифметичним квадратним коренем.
і називають арифметичним квадратним коренем.
Арифметичний корінь третього степеня називають кубічним коренем.
Властивості: 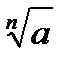 ·
· 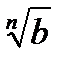 =
= 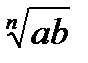 .
.
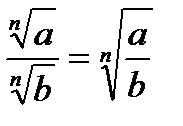 .
.
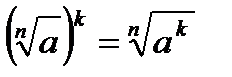 .
.
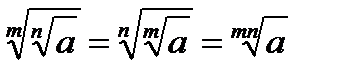 .
.
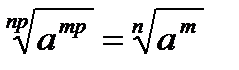 .
.
2. Взаємне розміщення прямої і площини в просторі. Ознака паралельності прямої і площини
| Взаємне розміщення прямої і площини | ||
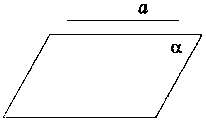 паралельні
a || α
паралельні
a || α
| 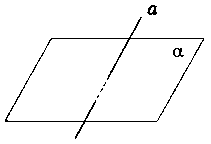 перетинаються перетинаються
|
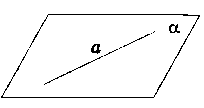 пряма лежить у площині пряма лежить у площині
|
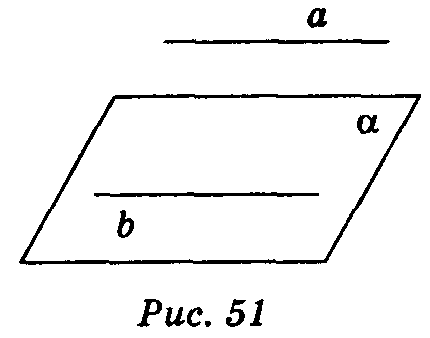 Теорема (ознака паралельності прямої і площини)
Теорема (ознака паралельності прямої і площини)
Якщо пряма, яка не належить площині, паралельна якій-небудь прямій у цій площині, то вона паралельна і самій площині.
Дано: а || b; b 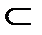 α (рис. 51).
α (рис. 51).
Довести: а || a.
|
|
|
|
|
Дата добавления: 2015-05-26; Просмотров: 2377; Нарушение авторских прав?; Мы поможем в написании вашей работы!