Теоретические основы решения. Проектный расчёт стержневой СИСТЕМЫ

Условие задачи

Проектный расчёт стержневой СИСТЕМЫ

В плоской стержневой системе, схемы которой даны в табл. 1.1, абсолютно жёсткий брус имеет три опорных стержня и несёт нагрузку известной величины. Исходные числовые значения взять из табл. 1.2.

Требуется:

1. Подобрать площади поперечного сечения опорных стержней из условия прочности по допускаемым напряжениям, считая допускаемое напряжение на сжатие 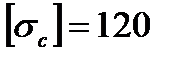МПа, на растяжение = 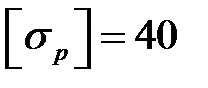МПа.

В задаче рассматривается расчёт стержней на прочность при растяжении-сжатии. Растяжение и сжатие возникает:

в опорных стержнях, поддерживающих какие либо конструкции (это сооружения, плоские и пространственные рамы, ─ в целом такие конструкции называют стержневыми системами);

в стержнях ферм (фермы − это системы из прямолинейных стержней, соединённых по концам шарнирами);

в элементах конструкций, имеющих вид прямого бруса постоянного или переменного сечения и нагруженных продольной нагрузкой. Например, как прямой брус при действии растягивающей силы рассматривают болты и винты, применяемые в механических соединениях; трос подъёмного механизма; как прямой брус изображают следующие элементы, воспринимающие продольную нагрузку: колонны зданий и оборудования, фабричные трубы, столбчатые фундаменты, которые сжаты собственном весом и верхней нагрузкой.

В случае растяжения-сжатия в поперечных сечениях бруса возникают только продольные силы N, которые и позволяют оценить сопротивление бруса внешним воздействиям и получить условие прочности. От продольных сил в поперечном сечении бруса появляются нормальные напряжения σ, равномерно распределённые по площади (рис. 1.1), поэтому значение напряжений σ определяют как отношение продольной силы к площади сечения A.

Эти напряжения не должны превышать допускаемого напряжения , поэтому для стержней условие прочности по допускаемым напряжениям записываем как

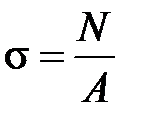
. (1.1)

По условию прочности (1.1) возможно выполнение трёх видов расчёта на прочность:

проектный расчёт (выполняется определение размеров сечения);

проверочный расчёт (вычисление напряжений и проверка прочности);

определение несущей способности (нахождение величины нагрузки).

Нужно помнить, что для пластичных материалов (например, для малоуглеродистых сталей) имеем одинаковые допускаемые напряжения на растяжение и сжатие, т. е. = = , а для хрупких материалов (например, для чугуна) допускаемые напряжения на растяжение 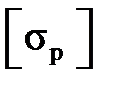и на сжатие различны.

Для правильного контроля работы конструкций надо знать, какие напряжения возникают не только в поперечном сечении, но и в любом наклонном к оси (рис. 1.1). Если стержень разрезать двумя плоскостями (рис. 1.1, а): плоскостью 1-1, перпендикулярной оси, и наклонной плоскостью 2-2, далее выделить полученную часть стержня (рис. 1.2, б) и рассмотреть её равновесие, то получим в наклонном сечении напряжения , параллельные σ и равные 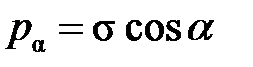. Разложим вектор напряжения на нормаль и касательную к наклонному сечению (рис. 1.1, б):

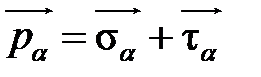
и получим, что при растяжении-сжатии в наклонных сечениях возникают и нормальные , и касательные 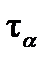напряжения, равные

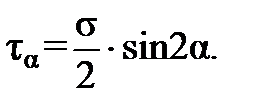, . (1.2)

а
б

Рис. 1.1

Формулы (1.2) показывают, что наибольшие нормальные напряжения возникают в поперечных сечениях, а наибольшие касательные ─ на площадках под углом , на которых , . Этот факт позволяет объяснить сопротивление растяжению и сжатию различных материалов.

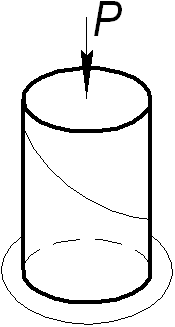
а ─ Стальной образец до и после сжатия	б ─ Чугунный образец до испытания и после разрушения от сжимающей силы

Рис. 1.2

Рассмотрим широко распространённые конструкционные материалы: сталь и чугун. Сталь, как пластичный материал, при сжатии получает пластичные (остаточные) деформации, которые происходят по линии действия касательных напряжений, и наибольший сдвиг получается от наибольших касательных напряжений под углом . При достижении по этому направлению предела текучести стали при сдвиге τ_т наблюдается интенсивный сдвиг, и образец принимает бочкообразную форму (рис. 1.2, а).. Таким образом, допускать предел текучести τ_т в стальных конструкциях опасно.

При сжатии чугунного образца (рис.1.2, б) наблюдается хрупкий скол по плоскости под углом 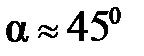к оси. Объяснить такое разрушение можно тем, что чугун хорошо сопротивляется сжатию и слабо сдвигу и растяжению. Образец срезается от действующих под углом касательных напряжений, когда они достигают предела прочности на сдвиг τ_В. Поэтому линия среза наклонена под 45⁰ к оси образца.

Дата добавления: 2015-06-04