Теоретические основы решения. Проверочный расчёт бруса

Условие задачи

Проверочный расчёт бруса

Для стального бруса, изображённого на рис. 2.1, а, известна внешняя нагрузка, заданы площадь поперечного сечения и длина (см. табл 2.1).

Требуется:

1. Построить эпюру продольных сил N.

2. Вычислить нормальные напряжения σ и проверить прочность при допускаемом напряжении [σ]=200Мпа.

3. Вычислить продольные перемещения, построить эпюру перемещений δ и проверить жёсткость при допускаемом перемещении [δ] = 0,5 мм. Принять модуль упругости E =2∙10⁵Мпа.

В задаче рассматривается брус, схема которого дана на рис 2, а. В начальном сечении бруса задана сосредоточенная сила Р, и по всей длине бруса действуют распределённая нагрузка интенсивности q. Например, в реальном брусе, расположенным вертикально, это может быть собственный вес, для которого вес куска бруса длиною 1 м является интенсивностью силы собственного веса, равной 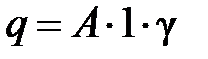, где А ¾ площадь сечения, 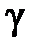¾ объёмный вес материала стержня.

Внешняя нагрузка направлена по оси бруса, тогда в поперечных сечениях бруса возникает только продольная сила N, по которой можно оценить сопротивление бруса внешним воздействиям и составить условия прочности и жёсткости. Если сила N положительна, то она вызывает растяжение, если отрицательна, ¾ сжатие.

Продольная сила это внутренняя сила, и её значение вычисляют методом сечений. Выполним вычисление продольной силы N для заданного бруса, выполняя последовательно правило РОЗУ метода сечений: р азрезать, о тбросить, з аменить, у равновесить.

Выполним разрез бруса на расстоянии z от свободного края (это будет текущее сечение) и изобразим правую часть (рис. 2.1, б). В текущем сечении поставим силу N, направив её от сечения, чтобы она растягивала отсечённую часть бруса, т.е. направление продольной силы ставим положительное.

Заметим, что, поставив силу N в текущем сечении, мы произвели замену воздействия отброшенной части бруса на оставленную. Составим уравнение равновесия. Как следует из вида нагрузки, при растяжении-сжатии имеем только одно уравнение равновесия, − это сумма проекций всех сил на продольную ось бруса:

. (2.1)

В нашем примере в это уравнение войдут внешние силы и и внутренняя продольная сила N. Уравнение принимает вид:

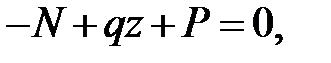
отсюда получим формулу продольной силы:

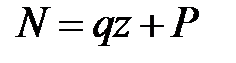. (2.2)

Как видно, продольная сила N в сечении равна алгебраической сумме проекций на ось z всех внешних сил, действующих по одну сторону от рассматриваемого сечения.

а Заданная схема бруса б Отсечённая часть в Эпюра продольной силы N г Эпюра продольных перемещений δ		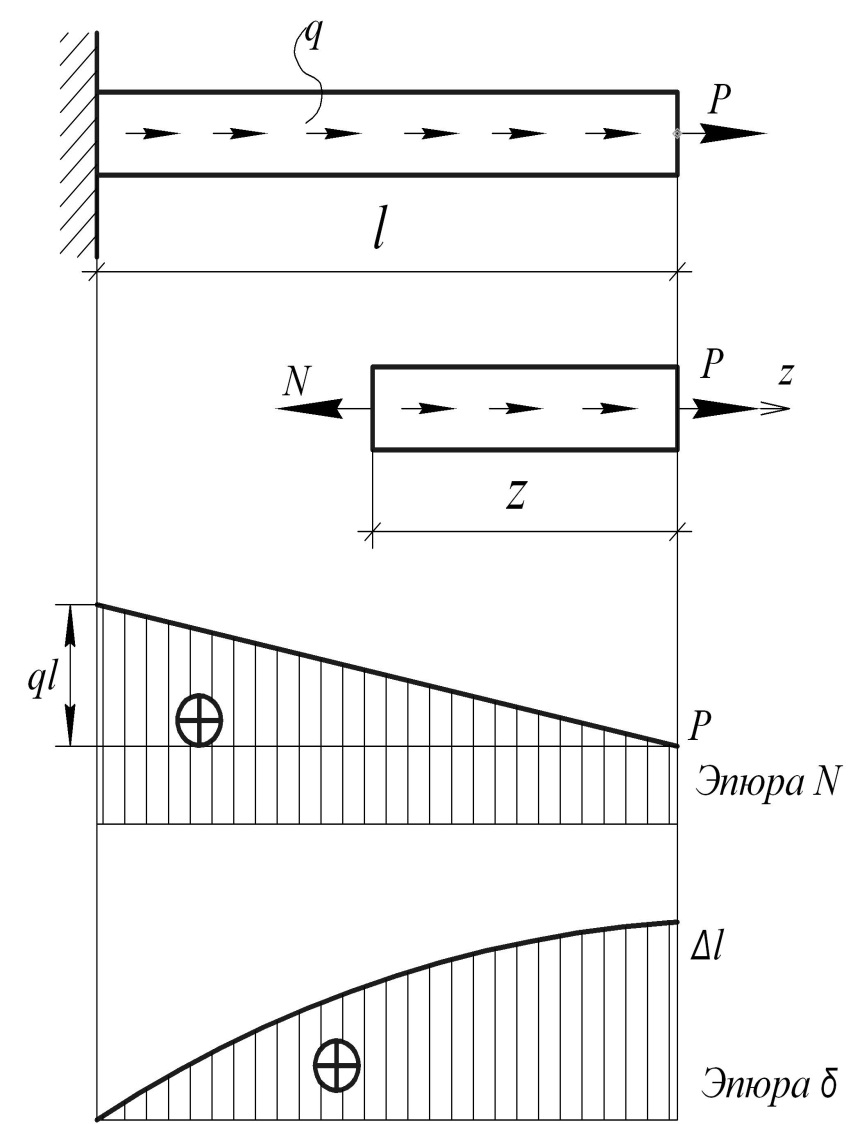N δ

Рис. 2.1

Принято изображать график изменения N вдоль оси, который называют эпюрой N. Этот график удобен, так как наглядно показывает изменение силы вдоль бруса и определяет опасное сечение: опасным является сечение, в котором продольная сила принимает максимальное значение (определяется максимальная растягивающая и максимальная сжимающая силы). Эти значения являются расчётными значениями силы и необходимы для составления условия прочности.

Для построения эпюры N вычислим значения силы в начале бруса (при z = 0) и в конце (при z = l).

Получим граничные значения продольной силы:

при z = 0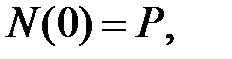

при z = l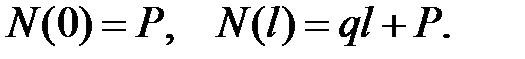

Отложив эти значения от базисной (нулевой) линии, проведённой под брусом, соединим значения согласно с (2.2) наклонной прямой и получим эпюру N (рис. 2.1, в).

При положительных значениях нагрузки, показанной на чертеже бруса, она выглядит нарастающей от свободного края по линейному закону. Реальная нагрузка вводит свои изменения в расчёты.

От продольных сил N в поперечном сечении бруса появляются нормальные напряжения σ, равномерно распределённые по площади (см. формулу 1.1).

Изменение значения продольный силы показано на эпюре N. В случае постоянной площади сечения вдоль бруса наибольшие растягивающие и наибольшие сжимающие напряжения будут в тех сечениях, где возникают наибольшая растягивающая (положительная) и наибольшая сжимающая (отрицательная) сила.

Заданный брус выполнен из стали, которая является пластичным материалом, имеющим одинаковые допускаемые напряжения на растяжение и сжатие, т. е. = = . Поэтому составляем одно условие прочности:

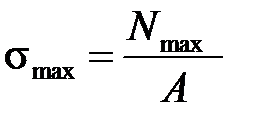
, (2.3)

где N _max ¾ расчётное значение продольной силы, оновыбирается по эпюре N как наибольшее по модулю значение N.

При эксплуатации конструкций происходит её деформирование, это вносит свои особенности в обслуживание и сохранение работоспособности, поэтому выполняют вычисление деформаций и проверку жёсткости конструкции.

В рассматриваемом брусе при действии продольной нагрузки изменяется длина, т.е. возникает продольная деформация.

Величина изменения длины как любого отрезка бруса длиною z таки всего бруса длиною l называется абсолютной продольной деформацией Δ l соответственно этого отрезка и всего бруса. Она вычисляется по формулам

∆ l (z) , ∆ l (l) , (2.4)

где E – модуль продольной упругости (или модуль Юнга): для стали и чугуна Е= 2∙10⁵МПа, для алюминиевых сплавов Е= 0,65 10⁵МПа; деформация Δ l обратно-пропорциональна величине EА, и ввиду этого величину EА называют жёсткостью сечения при растяжении-сжатии.

Подставим функцию продольной силы (2.2) в (2.4) и выполним интегрирование, получим

∆ l (z) = ,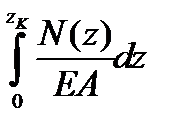

∆ l (l) . (2.5)

Здесь в выражении ∆ l (z) имеем функцию 2-го порядка по отношению переменной z (это результат действия распределённой нагрузки), значит, величина деформации отрезка z изменяется вдоль бруса по квадратичной зависимости от z. Если показать изменение деформации графически, то будет парабола.

За счёт продольной деформации Δ l происходят поступательные перемещения δпоперечных сечений бруса вдоль его оси. Для обеспечения нормальной эксплуатации необходимо, чтобы наибольшее перемещение δ_max не превышало допускаемого перемещения , в таком случае говорят, чтобы выполнялось условие жёсткости:

. (2.6)

Для нахождения δ_max вычисляют перемещения некоторых характерных сечений и изображают график изменения перемещений вдоль оси бруса, называемый эпюрой перемещений δ. Далее по эпюре перемещений выбирают δ_max и проверяют условие (2.6).

В нашем примере нужно знать перемещения заделки и свободного края бруса.

Перемещение заделки отсутствует, т. е. δ_зад = 0; свободный край бруса переместился на величину δ, равную деформации всего бруса ∆ l (l):

δ_зад +∆ l (l) . (2.7)

Для построения эпюры перемещений проведём базисную линию (см. рис. 2.1, г), параллельную оси бруса, отложим значение δ на свободном краю бруса и соединим эту точку с нулём для заделки параболой. Получили эпюру перемещений δ.

Дата добавления: 2015-06-04