DQ dQ dQ

где 0 есть Л/-мерный нулевой вектор. Допустим, что гессиан

(2.33)

dw²

это положительно определенная матрица. В этом случае вектор весов iv*

Q(w,,w₂)

минимизирует среднеквадратичную погрешность реализации (2.31). Из уравнения (2.32) следует, что для этого вектора справедливо равенство

Rw' = p. (2.34)

Равенство (2.34) называется нормальным уравнением. Если det R ф 0, то его решением оказывается вектор

iv* = R ¹р. (2.35)

При iv = iv* погрешность принимает минимальное значение, обо­значаемое Q* и равное

Q(iv*) = Q* = E[d₂(nj\ - 2w'^Tp + w'^T Riv*. (2.36)

Если подставить равенство (2.34) в выражение (2.36), то получим формулу для расчета минимальной среднеквадратичной погрешности реализации

Q* = E[cf₂(n)] - w'^Tp. (2.37)

Для нахождения оптимального вектора весов iv*, удовлетворяю­щего нормальному уравнению (2.34), требуется инвертировать матрицу автокорреляции R. Вместо этого можно использовать метод наискорей­шего спуска (см., например, [2, 6]), который широко применяется в теории оптимизации. В этом методе предусматривается итеративный расчет по­следовательных приближений оптимального вектора iv*. Обозначим iv(n) приближение, рассчитанное на л-й итерации

w(n)=[w,(n),.... w_N(n)]^T. (2.38)

Очередные коррекции компонентов вектора весов iv(n) должны производиться в направлении, противоположном знаку компонентов век­тора градиента

ЭО(иф7)) Г Э0(1У(п)) ЭО(1У(п)) 1^Г
Э(»(л)) [ dw^n) '""' dw_N(n) J ■ (²-³⁹)

Алгоритм наискорейшего спуска можно представить в виде

E[d>)]\

Рис. 2.8. Поверхность среднеквадратичной пофешности.

(2.40)

При подстановке формулы (2.32) в зависимость (2.40) получаем рекурсию

w(n + 1) = w(n) + [p~ Riv(n)], (2.41)

где константа ц > 0 определяет величину шага коррекции.

Можно показать (см., например, [8, 19]), что алгоритм наиско­рейшего спуска (2.41) сходится, т.е.

lim iv(n) = iv*, (2.42)

если шаг коррекции г) лежит в пределах

(2.43)

0 < Л <

где Я_тах - это наибольшее собственное значение матрицы автокорреля­ции R.

2.4 Системы типа Адалайн

30 Глава 2. Многослойные нейронные сети и алгоритмы их обучения

Кроме того, доказано, что скорость сходимости алгоритма наиско­рейшего спуска зависит от отношения наименьшего и наибольшего соб­ственных значений матрицы R. Если

Am. _s -i _ (2.44)

то алгоритм наискорейшего спуска сходится быстро. Если же

(2.45)

Лпах

то алгоритм наискорейшего спуска сходится медленно. 2.4.2. Адаптивный линейный взвешенный сумматор

Применение алгоритма (2.41) предполагает знание матрицы R и век­тора & В случае, когда эти величины неизвестны, следует заменить гради­ент (2.39) его приближением. Запишем рекурсивное выражение (2.40) в ви­де

w(n₊1)=-w(n)-l₄^M. (2.46)

Если в этой формуле заменить градиент его приближенным локальным значением (instantaneous estimate), т.е.

(2.47)

dw(n) dw(n) '

то получим рекурсию вида

(2.48)

Из выражений (2.24) и (2.25) следует, что

n +1) = Щп)+i\n{ n)[d(D) - w^T(n)u(n)]

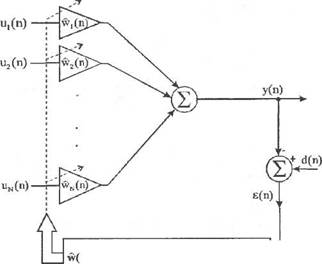
Рис. 2.9. Адаптивный линейный взвешенный сумматор.

Щ(п) w_N(n),

2) подсистемы, предназначенной для адаптивной коррекции этих весов и реализующей алгоритм LMS.

Параметр ц в алгоритме (2.50) подбирается так (см. [27]), чтобы выполнялось условие

"' ■■' ² --а-------------------- • (2-52)

—-----;—г- tcii/1-r-------- —- "l";-vv- (^-4У)

dw(n) dw(n)

При подстановке зависимости (2.49) в формулу (2.48) получаем
так называемый алгоритм LMS (Least Mean Square) в векторной форме
w(n + 1) = w(ri) + u(n)[d(n) - w^T(n)u(n)] (2.50)

или в скалярной форме

N

w_k(n + l)=w_k(n) + u_k(n) d(n)-^w_k(n)u_k(n) (2.51)

для к- 1..... N.

На рис. 2.9 представлен адаптивный линейный взвешенный сум­матор, известный в литературе под названием Адалайн (Adaptive Linear Neuron). Он состоит из двух основных частей:

1) линейного взвешенного сумматора с адаптивно корректиру­емыми весами

где TrR обозначает след матрицы R.

Дата добавления: 2015-06-04