Пример 2.1

N,

(0 =

(2-88)

где Я - так называемый коэффициент забывания (forgetting factor), зна­чение которого выбирается из интервала [0,1]. Обратим внимание на то, что степень влияния членов выражения (2.88) на его значение возраста­ет с увеличением номера члена. В ходе дальнейших рассуждений будем использовать обозначения, введенные в п. 2.5, с учетом особенностей, показанных на рис. 2.13, т.е.

(2.89)

а также

(2.90)

где /"-обратимая функция, t- 1,..., п, /'= 1,..., N_k, k- 1,..., L.

Глава 2. Многослойные нейронные сети и алгоритмы их обучения

2.6. Применение рекуррентного метода наименьших квадратов

Выражение (2.93) задает способ последовательного определения погрешностей в каждом слое, начиная с последнего. При дальнейших преобразованиях получаем последовательность равенств вида

t=

у

где

При использовании аппроксимации

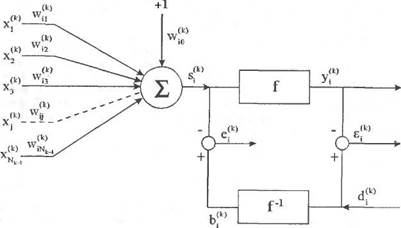
Рис. 2.13. Структура нейрона, применяемого для реализации алгоритма RLS.

Если рассчитать градиент меры погрешности и приравнять его к нулю, то получим уравнение

^vi \^П> f=1 j-

(2.91)

При использовании зависимостей (2.68) и (2.69) уравнение (2.91) принимает вид

' ^{(0 =}

=£/-;

¹"'-⁰-⁽²⁹²⁾

где

(2-93)

получаем нормальное уравнение л

векторная форма которого имеет вид

(2.95) = 0, (2.96)

где

t=-\ л

(2.97) (2.98) (2.99)

Уравнение (2.97) можно решить рекуррентным способом, без ин­вертирования матрицы R(^k\n). Это требует использования алгоритма RLS (например, [19]), согласно которому адаптивная коррекция всех ве­сов w№ производится согласно правилам

Глава 2. Многослойные нейронные сети и алгоритмы их обучения

2.6. Применение рекуррентного метода наименьших квадратов

(2.101) (2.102) (2.103)

СО/

Pi + f'²{s]^k)(n))x^ (n)PJ^k\n-P}^k\n) = X-\l-f'(s'_i

где/=1....... N_k, /с=1,...,L.

Начальные значения в алгоритме RLS, как правило, устанавлива­ются следующим образом:

Р(^к'(0) = 51, д»0, (2.104)

иЛ^к)(0) = 0. (2.105)

Начальные значения весов w№(0) нейронной сети могут также вы­бираться случайным способом из заранее установленного диапазона.

Сравним функционирование алгоритма обратного распростране­ния ошибки (2.86), модифицированного алгоритма (2.87) и алгоритма RLS (2.103). Для этого двухслойную нейронную сеть с сигмоидальными функциями будем использовать для имитации логической системы XOR и декодера 4-2-4. Процесс имитации должен длиться достаточно долго для того, чтобы значение погрешности Q(n) стало меньше заданного по­рога у, т.е.

(2.106)

Q(n) =

где N_L = 1 в случае логической системы XOR и N_L = 4 в случае декодера 4-2-4. На рисунках, иллюстрирующих результаты моделирования, под эпохой (ер) понимается количество итераций, равное числу различных пар векторов входных и эталонных сигналов (один цикл предъявления обучающей выборки). В обоих примерах каждая эпоха состоит из четы­рех итераций обучающего алгоритма.

а) Логическая система XOR. Нейронная сеть имеет 2 входа, 2 ней­
рона в скрытом слое и 1 выход. Заданный порог /равен 0.02. В отдель­
ные эпохи выделены следующие пары векторов входных и эталонных
сигналов:

(0,0; 0), (0,1; 1), (1,0; 1), (1,1; 0). Результаты моделирования представлены на рис. 2.14.

б) Декодер 4-2-4. Нейронная сеть имеет 4 входа, 2 нейрона
в скрытом слое и 4 нейрона в выходном слое. Заданный порог у ра­
вен 0,02. В отдельные эпохи выделены следующие пары векторов
входных и эталонных сигналов:

б)

120 160 200

в)

Рис. 2.14. Результаты моделирования логической системы XOR: а) алгоритм обратного распространения ошибки; б) модифицированный алгоритм обратного распространения ошибки (с учетом момента); в) алгоритм RLS.

юния

Глава 2. Многослойные нейронные сети и алгоритмы их oбy^

Список литературы

----- 0.9

Дата добавления: 2015-06-04