Адаптивный линейный взвешенный сумматор с сигмоидой на выходе

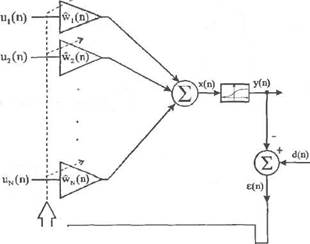
Выходной сигнал адаптивного линейного сумматора с сигмоидой на выходе (рис. 2.10) можно описать выражением

(2.53)

где функция f определяется формулой (2.6). Погрешность реализации (2.25) равна

Глава 2. Многослойные нейронные сети и алгоритмы их обучения

2.5. Алгоритм обратного распространения ошибки

w(n+1) = w(n) + Tie(n)f (x(n))u(n)

Рис. 2.10. Адаптивный линейный взвешенный сумматор с сигмоидой на выходе.

(2.54)

ф) = d(n) - f\

Для коррекции весов w^k), k = 1.......... N применим алгоритм LMS

(2.55) (2.56) (2.57) (2.58) (2.59)

в рекурсивной форме (2.48). В этом случае очевидно равенство

dw(n)

dw(n) '

а также

де(п) _ df(x(n)) _flx(nY. Эх(п) dw(n) dw(n) ^{к к} "dw(n)

где

x(n)=

u_k(n) =w^T(n)u(n).

dx(n)

Поскольку

dw(n)

= Ф),

то

При подстановке равенств (2.55) и (2.59) в рекурсивное выражение (2.48) получим следующий алгоритм адаптивной коррекции весов:

w{n + 1) = w{n) +7₁e(n)f'(x(n))u{n), (2.60)

либо в скалярной форме

\{п + 1) = w_k (л) + (n)f (x(n))u_k(n), (2.61)

для к = 1...... N. Если р = 1, то функция (2.6) отвечает условию

Г (х) - f(x)(1 - f(x)). (2.62)

Поэтому алгоритм (2.60) можно записать в форме

w_k(n + 1) = w, (n) + (n)f(x(n))(1 - f(x(n)))^(n) (2.63)

для /с= 1,..., Л/, где погрешность е(п) определяется выражением (2.54).

Алгоритмы (2.60) и (2.63) положены в основу метода обратного распространения ошибки, который подробно описывается в следую­щем разделе.

2.5. Алгоритм обратного распространения ошибки

Обсудим алгоритм обратного распространения ошибки [20], кото­рый позволяет обучать многогослойные нейронные сети. Этот алгоритм считается наиболее известным и чаще всего применяемым в искусствен­ных нейронных сетях.

На рис. 2.11. представлена многослойная нейронная сеть, со­стоящая из L слоев.

Рис. 2.11. Многослойная нейронная сеть.

В каждом слое расположено N_k элементов, к = 1..... L, обозначае­
мых ADf, i-\,..., N_k. Элементы ADf будем называть нейронами, причем
каждый из них может быть системой типа Адалайн с нелинейной функци­
ей (сигмоидой либо гиперболическим тангенсом) на выходе. Обсуждае-

Глава 2. Многослойные нейронные сети и алгоритмы их обучения

2.5. Алгоритм обратного распространения ошибки

мая нейронная сеть имеет Л/_о входов, на которые подаются сигналы ..., u_N (п), записываемые в векторной форме как

и = Ып)....... u_No(n)]^T, n=1,2,... (2.64)

Выходной сигнал /-го нейрона в к-м слое обозначается у/*'(п), /=1,..., N_k, /с=1,..., L.

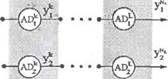
На рис. 2.12 показана детальная структура /-го нейрона в к-м слое. Нейрон ADf имеет Л/^ входов, образующих вектор

*»=[4^кНп),...,х%1(п)]^Т, (2.65)

причем х^'(п) = +1 для / = 0 и к = 1....... L. Обратим внимание на факт, что

входной сигнал нейрона AD^k связан с выходным сигналом (к — 1) слоя следующим образом:

для /с =

(2.66)

+ 1

для / = 0,/с = 1,...,/

W_kJ

На рис. 2.12 w^Xn) обозначает вес связи /-го нейрона, /= 1.... А/_А, распо­
ложенного в /с-м слое, которая соединяет этот нейрон су-м входным сиг­
налом xW(ri),j = 0, 1...... А/_м. Вектор весов нейрона AD¹? обозначим

... wW_kJn)]^T.k= 1......... L, /= 1....,

Выходной сигнал нейрона определяется как y]^k)( причем

(2.67) •* в л-й момент времени, п = 1,2,...

(2.68) (2.69)

Рис. 2.12. Структура нейрона

J=0

Отметим, что выходные сигналы нейронов в L-м слое

У1-(л),у£(п),...,у^(п) (2.70)

одновременно являются выходными сигналами всей сети. Они сравнива­ются с так называемыми эталонными сигналами сети

d![(n),4(n)..... <(л), (2.71)

в результате чего получаем погрешность

Ј,<^L)(n) = cf >(n)-y,(^L)(n),i=1.................... N_L. (2.72)

Можно сформулировать меру пофешности, основанную на сравне­нии сигналов (2.70) и (2.71), в виде суммы квадратов разностей (2.72), т.е.

i i (2-⁷³)

i=i /=1

Из выражений (2.68) и (2.69) следует, что мера погрешности (2.73) - это функция от весов сети. Обучение сети основано на адап­тивной коррекции всех весов w№(n) таким образом, чтобы минимизи­ровать ее значение. Для коррекции произвольного веса можно ис­пользовать правило наискорейшего спуска, которое принимает вид

^! ⁽²⁷⁴⁾

где мание, что

константа г] > 0 определяет величину шага коррекции. Обратим вни-

dQ(n)

9Q(n) 9Q(n)

Если ввести обозначение

дз]^кЦп) dwf\n) 9s|*

то получим равенство

(2.76) (2.77)

При этом алгоритм (2.74) принимает вид v\^k\n +1) = wf{n) + 2i₁8j^k\n)x^{k)(n).

w\

(2.78)

Способ расчета значения Si^k\n), заданного выражением (2.76), за­висит от номера слоя. Для последнего слоя получаем

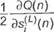
Глава 2. Многослойные нейронные сети и алгоритмы их обучения

2.6. Применение рекуррентного метода наименьших квадратов 37

_д5(Ц_{п]

Для произвольного слоя к ф L получаем)_ 1 ЭО(л) _ 1^¹ дСЦп)

(2.79)

слое (на основе выходных и эталонных сигналов), далее - в предпослед­нем и так вплоть до первого слоя. Начальные значения весов, образую­щих сеть, выбираются случайным образом и, как правило, устанавлива­ются близкими к нулю. Шаг коррекции ц чаще всего принимает большие значения (близкие единице) на начальных этапах процесса обучения, но впоследствии его следует уменьшать по мере того как веса приближают­ся к некоторым заранее определенным значениям. В литературе, посвя­щенной нейронным сетям (например, в [3]), рекомендуются различные модификации алгоритма обратного распространения ошибки. Одна из наиболее известных модификаций заключается во введении в рекурсию (2.86) дополнительного члена, называемого моментом:

w\^k

\n +1) = wf\n) + 2rie^(k\n)f{s\^k\n))x^(k\n)

(2.80)

m=1

Определим погрешность в к-м (не последнем) слое для /-го нейро­на в виде

^

_£<>)=

= 1..... L- 1. (2.81)

777=1

Если подставить выражение (2.81) в формулу (2.80), то получим

(2.82)

В записать	результате в виде	алгоритм	обратного распространения	ошибки можно
		(*}%)).	sj*»(n)=^^*»(n)xj*»(n) j=0	(2.83)
	(п) =	d N	f^L)(")-yJ ?>Г>(л	^L)(n) для/с = £, )w^(^\n) для/с = 1,...,/.-1 lilt * *	(2.84)
		m=1
			rj) = eJ^k>(n)f'(sW(n)),	(2.85)
	и	f'(n + 1) =	= ^»(л) + 2775/'^(»(л)х(.'^<»(л).	(2.86)

Название алгоритма связано со способом расчета погрешностей в конкретных слоях. Вначале рассчитываются погрешности в последнем

-1)], (2.87)

в котором параметр ae (0,1). Экспериментальные исследования показы­вают [24], что введение момента ускоряет сходимость алгоритма обрат­ного распространения ошибки.

2.6. Применение рекуррентного метода наименьших квадратов для обучения нейронных сетей

Обучение сети с использованием изложенного в п. 2.5 алгоритм обратного распространения ошибки требует большого количества итера­ций. Поэтому в литературных источниках приводятся сведения о различ­ных попытках создания более быстрых алгоритмов (см., например, [12]).

В работе [1] для обучения нейронных сетей применялся рекур­рентный метод наименьших квадратов (recursive least squares - RLS). В качестве меры погрешности использовалось выражение

Дата добавления: 2015-06-04