
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Система збіжних сил
|
|
|
|
Завдання 3. Сили, та лежать у площині, прикладені у точках, та і утворюють кути, та з додатним напрямом осі.
Зобразити сили у декартовій системі координат, знайти алгебраїчні проекції цих сил та записати вирази для векторів через геометричні проекції.
Дані взяти з таблиці С.1.б. Масштаб для величини сил взяти 1 см = 10 Н.
Таблиця С.1, б – вихідні дані для розв’язання задачі С.1 (завдання 3)
| № | 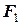 , Н , Н
| 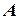
|  , º , º
| 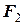 , Н , Н
| 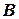
|  , º , º
|  , Н , Н
| 
|  , º , º
|
| (2,3) | 0º | (1,-4) | 30º | (-1,-2) | -120º | ||||
| (-2,1) | 50º | (-4,-1) | -40º | (3,0) | -90º | ||||
| (1,2) | 20º | (-1,-2) | 180º | (-1,4) | -130º | ||||
| (2,3) | 40º | (-3,3) | -20º | (-1,-2) | 0º | ||||
| (2,-1) | -50º | (-2,1) | 90º | (3,4) | -130º | ||||
| (-1,-2) | -130º | (3,-2) | 110º | (1,2) | 0º | ||||
| (2,-1) | -90º | (-4,-3) | 70º | (-2,-1) | 140º | ||||
| (-3,2) | 40º | (-2,-3) | 90º | (0,2) | -70º | ||||
| (-2,0) | 0º | (2,-4) | 75º | (4,3) | -110º | ||||
| (0,3) | -50º | (3,4) | -90º | (-4,-2) | 20º | ||||
| (3,-1) | -100º | (-1,1) | 140º | (4,2) | 180º | ||||
| (-1,0) | 90º | (3,1) | 130º | (2,-1) | -65º | ||||
| (1,-4) | 30º | (2,3) | 0º | (-1,-2) | -120º | ||||
| (-4,-1) | -40º | (-2,1) | 50º | (3,0) | -90º | ||||
| (-1,-2) | 180º | (1,2) | 20º | (-1,4) | -130º | ||||
| (-3,3) | -20º | (2,3) | 40º | (-1,-2) | 0º | ||||
| (-2,1) | 90º | (2,-1) | -50º | (3,4) | -130º | ||||
| (3,-2) | 110º | (-1,-2) | -130º | (1,2) | 0º | ||||
| (-4,-3) | 70º | (2,-1) | -90º | (-2,-1) | 140º | ||||
| (-2,-3) | 90º | (-3,2) | 40º | (0,2) | -70º | ||||
| (2,-4) | 75º | (-2,0) | 0º | (4,3) | -110º | ||||
| (3,4) | -90º | (0,3) | -50º | (-4,-2) | 20º | ||||
| (-1,1) | 140º | (3,-1) | -100º | (4,2) | 180º | ||||
| (3,1) | 130º | (-1,0) | 90º | (2,-1) | -65º | ||||
| (2,3) | 0º | (-1,-2) | -120º | (1,-4) | 30º | ||||
| (-2,1) | 50º | (3,0) | -90º | (-4,-1) | -40º | ||||
| (1,2) | 20º | (-1,4) | -130º | (-1,-2) | 180º | ||||
| (2,3) | 40º | (-1,-2) | 0º | (-3,3) | -20º | ||||
| (2,-1) | -50º | (3,4) | -130º | (-2,1) | 90º | ||||
| (-1,-2) | -130º | (1,2) | 0º | (3,-2) | 110º |
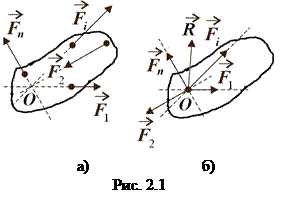 Система сил,лінії дії яких перетинаються в одній точці, називається збіжною. Нехай задано довільну систему збіжних сил (
Система сил,лінії дії яких перетинаються в одній точці, називається збіжною. Нехай задано довільну систему збіжних сил ( , які прикладені до твердого тіла (рис. 2.1, а). Перенесемо ці сили, як ковзні вектори, в точку
, які прикладені до твердого тіла (рис. 2.1, а). Перенесемо ці сили, як ковзні вектори, в точку  перетину ліній їх дії (рис. 2.1, б). Користуючись формулою (1.5), знайдемо рівнодійну
перетину ліній їх дії (рис. 2.1, б). Користуючись формулою (1.5), знайдемо рівнодійну 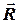 системи сил.
системи сил.
Для того, щоб тверде тіло під дією системи збіжних сил знаходилось у рівновазі, необхідно і достатньо, щоб виконувалась умова
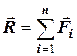 = 0. (2.1)
= 0. (2.1)
Векторному рівнянню (2.1) відповідають три скалярні:
 = 0, (2.2)
= 0, (2.2)
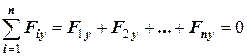 , (2.3)
, (2.3)
 , (2.4)
, (2.4)
де (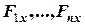 ), (
), (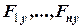 ) та (
) та ( ) – алгебраїчні проекції сил на декартові вісі
) – алгебраїчні проекції сил на декартові вісі 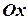 ,
, 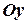 та
та 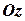 .
.
Отже, для того, щоб тверде тіло під дією збіжної системи сил знаходилось в рівновазі, необхідно та достатньо, щоб сума проекцій всіх сил на три взаємно перпендикулярні осі координат дорівнювали нулю.
У разі рівноваги системи збіжних сил, що лежать у площині, наприклад  , рівняння (2.4) виконується автоматично і умова рівноваги зводиться до рівності нулю суми проекцій цих сил на дві взаємно перпендикулярні осі
, рівняння (2.4) виконується автоматично і умова рівноваги зводиться до рівності нулю суми проекцій цих сил на дві взаємно перпендикулярні осі 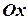 та
та 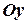 .
.
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 1295; Нарушение авторских прав?; Мы поможем в написании вашей работы!