
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Прямоугольные координаты
|
|
|
|
Вычисление длины дуги плоской кривой
Тренировка навыка использования запасного парашюта
Безусловно, навык использования запасного парашюта можно натренировать. И чем основательнее вы подойдете к этому процессу, тем надежнее и безопаснее вы будете чувствовать себя в воздухе. Вот несколько вариантов как можно подготовиться к успешному использованию запаски:
- Тренировать открывать запаску можно и на земле. Для этих целей используется простой тренажер: симулятор, который крепится к потолку. Ваш товарищ закрутит вас в одну из сторон, а потом отпустит. В этот момент лучше всего попросить его создавать вам дополнительную тряску и толки: так лучше всего сымитировать летную ситуацию. Ваша задача научиться выбрасывать запаску в разные стороны.
- Хотя бы один раз в полете находите у себя кольцо запаски, учитесь доставать его левой и правой рукой.
- Мысленно представляйте последовательность ваших действий в случае применение аварийного парашюта.
Рассмотреть различные аварийные ситуации: полное сложение купола, частичное сложение купола, столкновение. В каждом случае продумайте план выхода из ситуации. Такая практика поможет увеличить шансы успешного применения запаски.
Советы, данные в этой статье, нельзя назвать аксиомами. Каждая ситуация требует своего решения. Чем качественнее подготовка, тем выше вероятность успешного применения запасного парашюта. Конечно, лучше запаску не применять, но умение с ней обращаться делает полет безопасным.
Мягких посадок и чистого неба. И чтобы количество взлетов равнялось числу посадок!
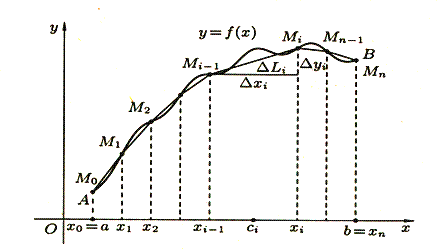
Пусть в прямоугольных координатах дана плоская кривая AB, уравнение которой y = f(x), где a ≤ x ≤ b. (рис 2)
Под длиной дуги AB понимается предел, к которому стремиться длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена ее стремиться к нулю.
Применим схему I (метод сумм).
1. Точками X 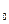 = a, X
= a, X 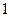 , …, X
, …, X 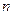 = b (X
= b (X 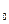 ≤ X
≤ X 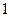 ≤ … ≤ X
≤ … ≤ X 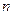 ) разобьем отрезок [a, b] на n частей. Пусть этим точкам соответствуют точки M
) разобьем отрезок [a, b] на n частей. Пусть этим точкам соответствуют точки M 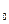 = A, M
= A, M 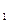 , …, M
, …, M 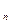 = B на кривой AB. Проведем хорды M
= B на кривой AB. Проведем хорды M 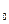 M
M 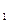 , M
, M 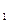 M
M 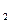 , …, M
, …, M 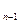 M
M 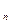 , длины которых обозначим соответственно через ΔL
, длины которых обозначим соответственно через ΔL 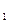 , ΔL
, ΔL 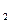 , …, ΔL
, …, ΔL 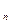 .
.
|
Получим ломанную M 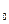 M
M 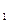 M
M 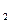 … M
… M 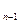 M
M 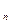 , длина которой равна L
, длина которой равна L 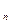 = ΔL
= ΔL 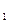 + ΔL
+ ΔL 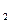 + … + ΔL
+ … + ΔL 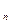 =
= 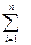 ΔL
ΔL  .
.
2. Длину хорды (или звена ломанной) ΔL  можно найти по теореме Пифагора из треугольника с катетами ΔX
можно найти по теореме Пифагора из треугольника с катетами ΔX 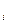 и ΔY
и ΔY  :
:
ΔL  =
= 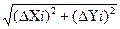 , где ΔX
, где ΔX 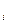 = X
= X 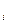 - X
- X 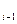 , ΔY
, ΔY  = f(X
= f(X 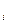 ) – f(X
) – f(X 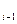 ).
).
По теореме Лагранжа о конечном приращении функции ΔY  =
= 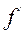 (C
(C 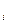 ) ΔX
) ΔX  , где C
, где C 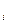
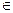 (X
(X 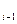 , X
, X 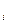 ). Поэтому
). Поэтому
ΔL  =
= 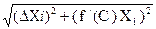 =
= 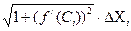 ,
,
а длина всей ломанной M 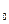 M
M 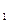 M
M 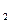 … M
… M 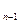 M
M 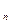 равна
равна
L 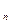 =
= 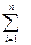 ΔL
ΔL  =
= 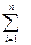
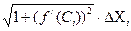 .
.
Длина кривой AB, по определению, равна L = 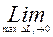 L
L 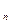 =
= 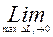
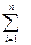 ΔL
ΔL  . Заметим, что при ΔL
. Заметим, что при ΔL 
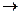 0 также и ΔX
0 также и ΔX 
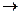 0 (ΔL
0 (ΔL  =
= 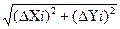 и следовательно | ΔX
и следовательно | ΔX  | < ΔL
| < ΔL  ). Функция
). Функция 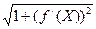 непрерывна на отрезке [a, b], так как, по условию, непрерывна функция f
непрерывна на отрезке [a, b], так как, по условию, непрерывна функция f 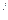 (X). Следовательно, существует предел интегральной суммы L
(X). Следовательно, существует предел интегральной суммы L 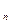 =
= 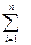 ΔL
ΔL  =
= 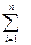
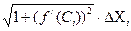 , кода max ΔX
, кода max ΔX 
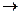 0:
0:
L = 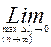
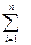
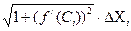 =
= 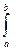
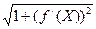 dx.
dx.
Таким образом, L = 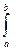
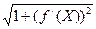 dx.
dx.
Пример: Найти длину окружности радиуса R. (рис 3)
Решение:
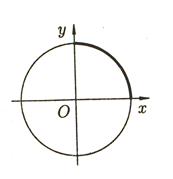 Найдем ¼ часть ее длины от точки (0;R) до точки (R;0). Так как y =
Найдем ¼ часть ее длины от точки (0;R) до точки (R;0). Так как y = 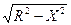 , ¼L =
, ¼L = 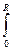
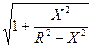 dx = R arcsin
dx = R arcsin 
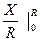 = R
= R 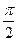 .
.
|
Значит L = 2 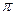 R.
R.
|
|
|
|
|
Дата добавления: 2015-06-26; Просмотров: 488; Нарушение авторских прав?; Мы поможем в написании вашей работы!