Работа переменной силы

Механические приложение определенного интеграла

Полярные координаты.

Пусть требует­ся определить площадь сектора ОАВ, ограниченного лу­чами 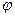= , 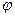= 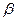и кривой АВ (рис 11), заданной в полярной системе координат уравнением r = r (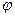), где r ( 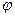) — функция, непрерывная на сегменте [ ; ].

Рис 11

Рис 12

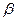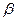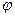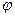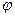
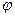
Разобьем отрезок [ ; ] на п частей точками = о< 1 <...< < 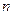= 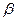и положим: Δ = — k = 1, 2,..., n. Наи­большую из этих разностей обозначим через : = max Δ . Разо­бьем данный сектор на п частей лучами = (k=1, 2,..., п — 1). Заменим k-й элементарный сектор круговым сектором радиуса r(), где .

Тогда сумма - приближенно площадь сектора OAB. Отсюда:

Пример. Найти площадь плоской фигуры, ограниченной кардиоидой г = a(1+соs ) (рис 12).

Решение. Учитывая симметричность кривой относительно полярной оси, по формуле получаем:

Пусть материальная точка М перемещается вдоль оси Ох под дей­ствием переменной силы F = F(х), направленной параллельно этой оси. Работа, произведенная силой при перемещении точки М из положения х = а в положение х = b (а <bЬ), находится по формуле

A =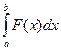

Пример. Какую работу нужно затратить, чтобы растянуть пру- жину на 0,05 м, если сила 100 Н растягивает пружину на 0,01 м?

Решение: По закону Гука упругая сила, растягивающая пружину, про­порциональна этому растяжению х, т. е. F = kх, где k— коэффициент пропорциональности. Согласно условию задачи, сила F = 100 Н растяги­вает пружину на х = 0,01 м; следовательно, 100 = k 0,01, откуда k = 10000; следовательно, F =10000 х.

Искомая работа на основании формулы A =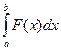

равна

A =

Пример. Найти работу, которую необходимо затратить, чтобы выкачать через край жидкость из вертикального цилиндрического резер­вуара высоты Н м и радиусом основания Rм (рис 13).

Решение: Работа, затрачиваемая на поднятие тела весом р на высоту h, равна р • Н. Но различные слои жидкости в резервуаре находятся на различных глубинах и высота поднятия (до края резервуара) различных слоев не одинакова.

Для решения поставленной задачи применим схему II (метод дифференциала). Введем систему координат.

1. Работа, затрачиваемая на выкачивание из резер­вуара слоя жидкости толщиной х (0 ≤ х ≤ Н), есть функция от х, т. е. А = А(х), где (0 ≤ х ≤ Н)(A(0) = 0, A (H) = А₀).

2. Находим главную часть приращения ΔA при из­менении х на величину Δх = dx, т. е. находим диффе­ренциал d А функции А(х).

Ввиду малости dх считаем, что “элементарный” слой жидкости находится на одной глубине х (от края резервуара). Тогда d А = dрх, где d р — вес этого слоя; он равен g АV, где g — ускорение свободногопадения, 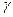— плотность жидкости, dv — объем “элементарного” слоя жидкости (на рисунке он выделен), т. е. d р = g . Объем указанного слоя жидкости, очевидно, равен , где dx— высота цилиндра (слоя), 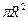— площадь его основания, т. е. dv= .

Таким образом, d р = . и

3) Интегрируя полученное равенство в пределах от х = 0 до х = Н, находим

A

Дата добавления: 2015-06-26