Интегральное исчисление в экономике

В курсе микроэкономики часто рассматривают так называемые предельные величины, т.е. для данной величины, представляемой некоторой функцией у =f(x), рассматривают ее производную f'x. Например, если дана функция издержек С в зависимости от объема qвыпускаемого товара С = С(q), то предельные издержки будут за­даваться производной этой функции МС = С'(q). Ее экономический смысл - это издержки на производство дополнительной единицы выпускаемого товара. Поэтому часто приходится находить функ­цию издержек по данной функции предельных издержек.

Пример. Дана функция предельных издержек МС = Зq² – 48q + 202, 1 ≤ q ≤ 20. Найти функцию издержек С = С(q) и вычис­лить издержки в случае производства 10 единиц товара, если из­вестно, что издержки для производства первой единицы товара со­ставили 50 руб.

Решение. Функцию издержек находим интегрированием:

C(q) = ,

где константа Со находится из данного условия С(1) = 50, так что С₀ = 50, поскольку интеграл обращается в нуль. Интегрируя, полу­чим функцию издержек

C(q) = q .

Подставляя q = 10 в полученную формулу, находим искомое значение

С(10) = 670.

Еще одним примером приложения определенного интеграла является нахождение дисконтированной стоимости денежного потока.

Допустим вначале, что для каждого дискретного момента времени t= 1, 2, 3,... задана величина денежного потока R((t). Если ставку процента обозначить через р, то дисконтированную стоимость каждой из величин R(1), R(2), R(3),... найдем по известным формулам:

R(1)(1 + p) , R(2)(1 + p) , R(3)(1 + p) , ….

Тогда дисконтированную стоимость денежного потока найдем, суммируя эти величины:

П = ,

где п - общее число периодов времени.

В непрерывной модели время изменяется непрерывно, т.е. для каждого момента времени 0 ≤ t ≤ Т, где [0, T] - рассматриваемый период времени, задана величина I(t) - скорость изменения денеж­ного потока (т.е. величина денежного потока за промежуток времени от t до t + dt приближенно равна I (t)dt. Для получения ве­личины П изменим формулу П = .А именно, знак суммирования заменим на знак определенного интеграла, формулы вычисления дисконтированной стоимости в дискретном случае заменим на их непрерывный аналог, и тогда формула П = , примет следую­щий вид:

П = .

Пример. Под строительство гидроэлектростанции задан непрерывный денежный поток со скоростью I(t) = -t² +20t +5 (млрд руб./год) в течение 20 лет с годовой процентной ставкой р = 5%. Найти дисконтированную стоимость этого потока.

Решение. По формуле П = имеем

П = .

Чтобы вычислить этот интеграл, выполним сначала замену переменной:

s = -0,05t, t = -20s, dt = -20ds.

При этом новые пределы интегрирования получаются подстановкой старых пределов в формулу замены: s = 0, s = -1. Имеем

-

П = -20 (- 400s² – 400s + 5)e = 20 (- 400s² – 400s +5)e ds.

К последнему интегралу применим формулу интегрирования по частям, полагая и = -400s - 400s + 5, dи = (-800s - 400)ds, dv = e ds, v= е . Поэтому

П = 20 ((-400s² - 400s + 5)е + е (800s + 400)ds.

В первом слагаемом подставим пределы интегрирования, а ко вто­рому слагаемому еще раз применим формулу интегрирования по частям, полагая и = 800s + 400, d и = 800ds. Имеем

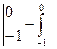П = 20 (5 – 5e + (800s + 400)e 800e ds) =

= 20(5 - 5е - 1 +400 + (800 - 400)e - 1 - 800 + 800е - 1) =

= 20(1195е- 1 -395).

Окончательно получим П = 892 (млрд руб.).

Далее рассмотрим некоторую модель экономического роста, предложенную Е.Д. Домаром. Основные допущения этой моде сформулированы ниже.

1. Всякое изменение величины скорости денежного потока I(t) влияет как на совокупный спрос, так и на изменение объема производства.

2. Скорость изменения величины спроса Y(t) пропорциональна производной скорости денежного потока с коэффициентом пропорциональности K = 1/s, где s - предельная величина накопления. Это предположение можно записать в виде уравнения

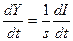
3 Экономический потенциал к (т.е. величина стоимости това-которые можно произвести) пропорционален объему оборот-' средств К с коэффициентом пропорциональности р, k = рК. Дифференцируя по t, получим

.

В модели Домара предполагается, что весь экономический по­тенциал полностью используется, иными словами, У = к. Диффе­ренцируя по t, получим

.

Подставляя 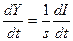и в , имеем

= pI, .

Чтобы найти функцию I(t) из уравнения = pI, , проинтегрируем обе части последнего равенства по t от 0 до t. Получим

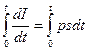, или ln|I(t)| = pst ,

Откуда ln|I| = ln|I(0)| + pst. Потенцируя последнее равенство, получим окончательное выражение для I(t):

I(t) = I(0)e ,

где I(0) – это скорость денежного потока в начальный момент времени.

Таким образом, для того чтобы поддерживать равновесие между объемом производимых благ и совокупным спросом на них, скорость денежного потока должна расти с экспоненциальной скоростью согласно формуле

I(t) = I(0)e

Заключение

Рассмотренные выше примеры практических задач, дают нам ясное представление значимости определенного интеграла для их разрешимости.

Трудно назвать научную область, в которой бы не применялись методы интегрального исчисления, в общем, и свойства определенного интеграла, в частности. Так в процессе выполнения курсовой работы нами были рассмотрены примеры практических задач в области физики, геометрии, механики, биологии и экономики. Конечно, это еще далеко не исчерпывающий список наук, которые используют интегральный метод для поиска устанавливаемой величины при решении конкретной задачи, и установлении теоретических фактов.

Также определенный интеграл используется для изучения собственно самой математики. Например, при решении дифференциальных уравнений, которые в свою очередь вносят свой незаменимый вклад в решение задач практического содержания. Можно сказать, что определенный интеграл - это некоторый фундамент для изучения математики. Отсюда и важность знания методов их решения.

Из всего выше сказанного понятно, почему знакомство с определенным интегралом происходит еще в рамках средней общеобразовательной школы, где ученики изучают не только понятие интеграла и его свойства, но и некоторые его приложения.

Дальнейшая наша работа над данной темой планируется именно в направлении рассмотрения методики и линий изучения определенного интеграла в школе.

Литература

1. Баврин И.И. Высшая математика – М.: Просвещение, 1993. – 319.

2. Бермантт А.Ф., Араманович И.Г. Краткий курс математического анализа для втузов - М.: Наука, 1971. - 736с.

3. Красс М.C Основы математики и ее приложения в экономическом образовании

4. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов, Том 2 -М.:Наука, 1985.-560с.

5. Письменный Д.Т. Конспект лекций по высшей математике – M.: Айрис – пресс, 2003. – 288 c.

6. Солодовников А.С., Бабайцев В.А Математика в экономики – M.: Финансы и статистика, 2005. – 560c.

7. Фихтенгольц Том 2

8. Шипачёв В.С. Высшая математика - М: Наука, 2003 – 684c.

Дата добавления: 2015-06-26