Вычисление выборочных характеристик распределения (непосредственно)

Для вычисления средней арифметической, дисперсии, коэффициентов ассиметрии и эксцесса рекомендуется следующий порядок вычислений.

Заменяем интервальный ряд дискретным, для чего все значения признака в пределах интервала приравниваем к его серединному значению, и считаем, что частота относится к середине интервала. Значения середин интервалов равны .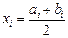

Для удобства вычислений целесообразно составить вспомогательную таблицу 1.3. Заменяя середины интервалов заносят в графу 1, соответствующие частоты в графу и т.д.

Интервалы
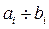
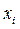
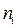
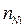
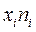
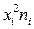
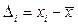
4,97-5,08 5,08-5,19 5,19-5,30 5,30-5,41 5,41-5,52 5,52-5,63 5,63-5,74 5,74-5,85	5,03 5,14 5,25 5,36 5,47 5,58 5,69 5,80			10,06 15,42 63,00 101,84 158,63 100,44 73,97 23,20	50,60 79,26 330,75 545,86 867,71 560,46 420,89 134,56	-0,4356 -0,3256 -0,2156 -0,1056 0,0044 0,1144 0,2244 0,3344
				546,56	2990,09

Таблица 1.3 Вспомогательная таблица для вычисления выборочных характеристик

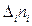
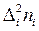
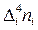
-0,8712 -0,9768 -2,5872 -2,0064 0,1276 2,0592 2,9172 1,3376	0,37949 0,31805 0,55780 0,21188 0,00056 0,23557 0,65462 0,44729	-0,1653 -0,10356 -0,12026 -0,02237 0,00000 0,02695 0,14690 0,14957	0,07201 0,03372 0,025928 0,00236 0,00000 0,00308 0,03296 0,05002
	2,80526	0,08808	0,22008

В таблице .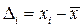

Пользуясь таблицей 1.3, вычислим среднюю арифметическую: 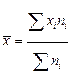. В нашем примере 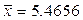млн. руб. и характеризует среднее положение наблюдаемых значений. Выборочный центральный момент к-го порядка равен 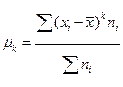. Для проверки правильности вычисления 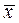и ввода в микрокалькулятор значений 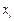, 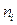рассчитывают:

В нашем примере тождество выполняется. В итоговой строке столбца 4 табл. 1.3. имеем 0.

В данном примере .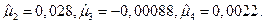

Выборочная дисперсия 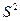равна центральному моменту второго порядка:

= = .

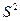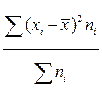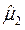В нашем примере 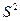=0,028, а выборочное среднее квадратичное отклонение 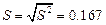млн.руб.

Дисперсию можно подсчитать и по-другому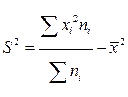

В нашем примере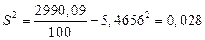

Выборочные коэффициенты асимметрии

.

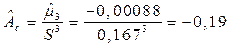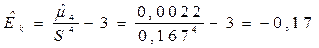
Дата добавления: 2015-06-26