Расчет теоретической нормальной кривой распределения

Приведем один из способов расчета теоретического нормального распределения по двум найдем выборочным характеристикам x и S эмпирического ряда.

При расчете теоретических частот 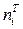за оценку математического ожидания 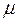и среднего квадратичного отклонения 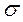нормального закона распределения принимают значения соответствующих выборочных характеристик и S, т.е.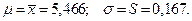

Теоретические частоты находят по формуле , где n—объем; 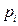-вероятность попадания значения нормально распределенной случайной величины в i -й интервал.

Вероятность 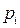определяется по формуле

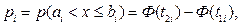где - интегральная функция Лапласа находится по таблице для .

Для вычисления вероятности 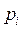и теоретических частот 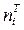составим таблицу 1.5.

Примечание. При использование критерия Пирсона общее число наблюдений должно быть достаточно большим () и интервалы должны быть достаточно заполнены частотами. Если отдельные теоретические частоты на концах распределения окажутся малыми (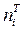 <5), то при вычислении 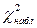. Необходимо объединить такие интервалы, сложив соответствующие частоты.

Построим теоретическую нормальную кривую 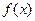на рис 1.1. Для этого из середины частных интервалов восстановим перпендикуляры высотой 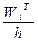(табл.1.5. графа 10), где . На рис 1.1 концы этих перпендикуляров отмечены точками. Полученные точки соединены плавной кривой.

Сравнение гистограммы и нормальной кривой наглядно показывает согласованность между теоретическим и эмпирическим распределением.

Интервалы
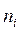
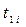
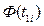
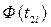
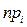
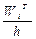
4,97-5,08			-2,39	-0,5	-0,4913	0,0087	0,87		0,09
5,08-5,19		-2,39	-1,71	-0,4913	-0,4564	0,0349	3,49		0,27
5,19-5,30		-1,71	-1,03	-0,4564	-0,3485	0,1079	10,9		1,00
5,30-5,41		-1,03	-0,35	-0,3485	-0,1368	0,2117	21,17		1,91
5,41-5,52		-0,35	0,33	-0,1368	0,1293	0,2661	26,61		3,45
5,52-5,63		0,33	1,02	0,1293	0,3461	0,228	22,28		2,00
5,63-5,74		1,02	1,70	0,3461	0,4554	0,1093	1,98		1,00
5,74-5,85		1,70		0,4554	0,5	0,0446	4,46		0,36

Таблица 1.5. Расчет теоретической нормальной кривой распределения.

Дата добавления: 2015-06-26