Непрерывная информационная поддержка

поставок и жизненного цикла (CALS)

Термин CALS (Continuous Acquisition and Lifecycle Support — не­прерывная информационная поддержка поставок и жизненного цик­ла) означает совокупность принципов и технологий информационной поддержки жизненного цикла продукции на всех его стадиях. Русско­язычный аналог понятия CALS — информационная поддержка жиз­ненного цикла изделий. В последнее время за рубежом наряду с CALS используется также термин Product Lifecycle Management (PLM) [6].

Целью применения CALS-технологий как инструмента организа­ции и информационной поддержки всех участников создания, произ­водства и пользования продуктом является повышение эффективнос­ти их деятельности за счет ускорения процессов исследования и раз­работки продукции, придания изделию новых свойств, сокращения издержек при производстве продукции, повышения уровня сервиса в течение ее эксплуатации и технического обслуживания.

Стратегия CALS объединяет в себе: применение современных ин­формационных технологий, реинжиниринг бизнес-процессов, при­менение методов «параллельной» разработки, стандартизацию в об­ласти совместного использования данных и электронного обмена дан­ными.

В дословном переводе аббревиатура CALS означает «непрерыв­ность поставок продукции и поддержки ее жизненного цикла». «Не­прерывность поставок» требует и подразумевает оптимизацию процес­сов взаимодействия «заказчика и поставщика» в ходе разработки, про­ектирования и производства сложной продукции, срок жизни которой, с учетом различных модернизаций, составляет десятки лет. Для обес­печения эффективности, а также сокращения затрат средств и време­ни, процесс взаимодействия заказчика и поставщика должен быть дей­ствительно непрерывным.

Вторая часть определения CALS — «поддержка жизненного цик­ла» — заключается в оптимизации процессов обслуживания, ремонта, снабжения запасными частями и модернизации. Поскольку затраты на поддержку сложного наукоемкого изделия в работоспособном со­стоянии часто равны или превышают затраты на его приобретение, принципиальное сокращение «стоимости владения» обеспечивается инвестициями в создание системы поддержки жизненного цикла.

В развитых странах CALS рассматривается как комплексная сис­темная стратегия повышения эффективности процессов, связанных с промышленной продукцией, непосредственно влияющая на ее конку­рентоспособность. Повышение конкурентоспособности достигается за счет уменьшения затрат (цены изделия), сокращения сроков вывода новых образцов на рынок, улучшения качества продукции за счет сквоз­ной поддержки ее жизненного цикла. Применение стратегии CALS является условием выживания предприятий в условиях растущей кон­куренции, в том числе на международных рынках, в ближайшие не­сколько лет.

Технологии CALS активно применяются, прежде всего, при разра­ботке и производстве сложной наукоемкой продукции, создаваемой интегрированными промышленными структурами, включающими в себя НИИ, КБ, основных подрядчиков, субподрядчиков, поставщи­ков готовой продукции, потребителей, предприятия технического об­служивания, ремонта и утилизации продукции.

Вместе с тем применение CALS-технологий позволяет эффектив­но, в едином ключе решать проблемы обеспечения качества выпускае­мой продукции, поскольку электронное описание процессов разработ­ки, производства, монтажа полностью соответствует требованиям меж­дународных стандартов ISO-9000, реализация которых гарантирует выпуск высококачественной продукции.

Потребность в едином информационном пространстве вызвала к жизни следующий этап развития ИТ, основанных на концепции ин­формационной поддержки жизненного цикла продукта, которая воп­лотилась в рамках технологии CALS и реализуется совокупностью систем ИТ.

Информационное взаимодействие всех участников жизненного цикла продукта должно осуществляться в едином информационном пространстве, использующем концепции открытых архитектур, меж­дународных стандартов и программ обмена данными. Первые шаги по организации такого пространства связаны с CALS-технологиями. Эти технологии применяются как инструмент организации и информаци­онной поддержки всех участников создания, производства и пользо­вания продуктом. Целью их применения является повышение эффек­тивности деятельности за счет ускорения процессов исследования и разработки продукции, придания изделию новых свойств, сокраще­ния издержек производства и эксплуатации продукции, повышения уровня сервиса при эксплуатации и техническом обслуживании.

Следующей проблемой, которую можно решить на основе исполь­зования CALS-технологий, является проблема качества, которая сво­дится в основном к достоверности и качеству информации, циркули­рующей на всех стадиях жизненного цикла изделия: проектирования, внедрения, эксплуатации и утилизации. Имея достоверную информа­цию, руководство может контролировать ход изготовления и вовремя влиять на процессы производства.

Для информационного сопровождения изделия в течение жизнен­ного цикла формируется набор данных, который включает в себя информацию о структуре изделия, его характеристиках и свойствах, орга­низационную информацию для целей управления, информацию о контрольных испытаниях и всю документацию, которая появляется с мо­мента зарождения изделия до его утилизации.

Весь объем информации об изделии распределяется по этапам жиз­ненного цикла и фиксируется в виде следующих данных: конструк­торские, технологические, производственные, о качестве, логистичес­кие и эксплуатационные. Организация и использование таких разно­родных данных требует использования единого стандарта, которым является международный стандарт ISO 10303 STEP (ГОСТ Р ИСО 10303) — Стандарт о представлении информации об изделии и спосо­бам работы с ней.

Вот некоторые количественные оценки эффективности внедрения CALS в промышленности США: прямое снижение затрат на проекти­рование — от 10 до 30%; сокращение времени разработки изделий — от 40 до 60%, времени вывода новых изделий на рынок — от 25 до 75%; уменьшение доли брака и объема конструктивных изменений — от 20 до 70%; снижение затрат на подготовку технической документации — до 40%, а затрат на разработку эксплуатационной документации — до 30%.

По зарубежным данным, потери, связанные с несовершенством ин­формационного взаимодействия с поставщиками, только в автомобиль­ной промышленности США составляют около 1 млрд дол. в год. Анало­гичные потери имеют место и в других отраслях промышленности.

В тех же источниках указывается, что затраты на разработку реак­тивного двигателя GE 90 для самолета «Боинг-777» составили 2 млрд дол., а создание новой модели автомобиля компании «Форд» стоит от 3 до 6 млрд дол. Это означает, что экономия от снижения прямых зат­рат на проектирование только по двум указанным объектам может со­ставить от 500 млн до 2,2 млрд дол.

Как видим, внедрение CALS-технологий приводит к существенной экономии и получению дополнительной прибыли, поэтому эти техно­логии и их отдельные компоненты широко применяются в промыш­ленности развитых стран. Так, из числа 500 крупнейших мировых ком­паний, входящих в перечень Fortune 500, около 100% используют та­кой важнейший компонент CALS, как средства PDM (Product Data Management — управление данными об изделии). Среди предприятий с годовым оборотом свыше 50 млн. дол. такие системы используют бо­лее 80%.

связи с большими объемами ожидаемой экономии и дополнительных прибылей в эту сферу привлекаются значительные инвести­ции, измеряемые миллиардами долларов. По данным зарубежных источников, инвестиции правительства США в сферу CALS-технологий составляют около 1 млрд дол. в год. Затраты других стран меньше, од­нако, например, правительство Финляндии затратило на национальную программу в этой области свыше 20 млн дол. и примерно такую же сумму (около 25 млн дол.) вложили в нее частные компании. Корпорация «General Motors» в течение 1990—1995 гг. израсходовала на эти цели 3 млрд дол. Средние затраты на один проект, посвященный решению локальной задачи в области CALS-технологий (например, разработка стандарта или программы), составляют 1,2—1,5 млн дол. при среднем сроке выполнения от двух до четырех лет. Эти цифры свидетельству­ют о том, какое значение придают на Западе проблематике, связанной с CALS-технологиями.

Поиск решения в среде EXCEL

Мощным средством анализа данных Excel является надстройка Solver (Поиск решения). С ее помощью можно определить, при каких значениях указанных влияющих ячеек формула в целевой ячейке принимает нужное значение (минимальное, максимальное или равное какой-либо величине). Для процедуры поиска решения можно задать ограничения, причем не обязательно, чтобы при этом использовались те же влияющие ячейки. Для расчета заданного значения применяются различные математические методы поиска. Вы можете установить режим, в котором полученные значения переменных автоматически заносятся в таблицу. Кроме того, результаты работы программы могут быть оформлены в виде отчета.
Программа Поиск решений (в оригинале Excel Solver) – дополнительная надстройка табличного процессора MS Excel, которая предназначена для решения определенных систем уравнений, линейных та нелинейных задач оптимизации, используется с 1991 года.
Размер задачи, которую можно решить с помощью базовой версии этой программы, ограничивается такими предельными показателями:

количество неизвестных (decision variable) – 200;

количество формульных ограничений (explicit constraint) на неизвестные – 100;

количество предельных условий (simple constraint) на неизвестные – 400.

Разработчик программы Solver компания Frontline System уже давно специализируется на разработке мощных и удобных способов оптимизации, встроенных в среду популярных табличных процессоров разнообразных фирм-производителей (MS Excel Solver, Adobe Quattro Pro, Lotus 1-2-3).
Высокая эффективность их применения объясняется интеграциею программы оптимизации и табличного бизнес-документа. Благодаря мировой популярности табличного процессора MS Excel встроенная в его среду программа Solver есть наиболее распространенным инструментом для поиска оптимальных решений в сфере современного бизнеса.
По умолчанию в Excel надстройка Поиск решения отключена. Чтобы активизировать ее в Excel 2007, щелкните значок Кнопка Microsoft Office, щелкните Параметры Excel, а затем выберите категорию Надстройки. В поле Управление выберите значение Надстройки Excel и нажмите кнопку Перейти. В поле Доступные надстройки установите флажок рядом с пунктом Поиск решения и нажмите кнопку ОК.

В Excel 2003 и ниже выберите команду Сервис/Надстройки, в появившемся диалоговом окне Надстройки установите флажок Поиск решения и щелкните на кнопке ОК. Если вслед за этим на экране появится диалоговое окно с предложением подтвердить ваши намерения, щелкните на кнопке Да. (Возможно, вам понадобится установочный компакт-диск Office).

Процедура поиска решения
1. Создайте таблицу с формулами, которые устанавливают связи между ячейками.

2. Выделите целевую ячейку, которая должна принять необходимое значение, и выберите команду:
- В Excel 2007 Данные/Анализ / Поиск решения;
- В Excel 2003 и ниже Tools > Solver (Сервис > Поиск решения). Поле Set Target Cell (Установить целевую ячейку) открывшегося диалогового окна надстройки Solver (Поиск решения) будет содержать адрес целевой ячейки.
3. Установите переключатели Equal To (Равной), задающие значение целевой ячейки, — Мах (максимальному значению), Min (минимальному значению) или Value of (значению). В последнем случае введите значение в поле справа.
4. Укажите в поле By Changing Cells (Изменяя ячейки), в каких ячейках программа должна изменять значения в поисках оптимального результата.
5. Создайте ограничения в списке Subject to the Constraints (Ограничения). Для этого щелкните на кнопке Add (Добавить) и в диалоговом окне Add Constraint (Добавление ограничения) определите ограничение.

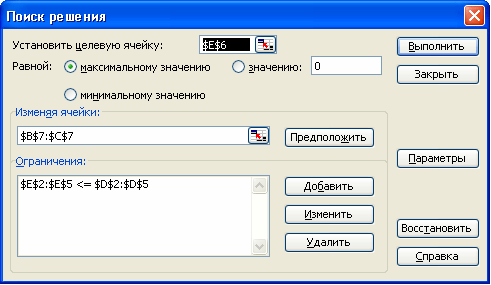
6. Щелкните на кнопке на кнопке Options (Параметры), и в появившемся окне установите переключатель Неотрицательные значения (если переменные должны быть позитивными числами), Линейная модель (если задача, которую вы решаете, относится к линейным моделям)

7. Щелкнув на кнопке Solver (Выполнить), запустите процесс поиска решения.

8. Когда появится диалоговое окно Solver Results (Результаты поиска решения), выберите переключатель Keep Solve Solution (Сохранить найденное решение) или Restore Original Values (Восстановить исходные значения).
9. Щелкните на кнопке ОК.

Параметры средства Поиск решения
Максимальное время - служит для ограничения времени, отпущенного на поиск решения задачи. В этом поле можно ввести время в секундах, не превышающее 32 767 (примерно девять часов); значение 100, используемое по умолчанию, вполне приемлемо для решения большинства простых задач.

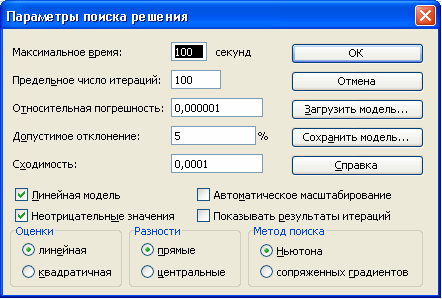
Предельное число итераций - управляет временем решения задачи путем ограничения числа вычислительных циклов (итераций).
Относительная погрешность - определяет точность вычислений. Чем меньше значение этого параметра, тем выше точность вычислений.
Допустимое отклонение - предназначен для задания допуска на отклонение от оптимального решения, если множество значений влияющей ячейки ограничено множеством целых чисел. Чем больше значение допуска, тем меньше времени требуется на поиск решения.
Сходимость - применяется только к нелинейным задачам. Когда относительное изменение значения в целевой ячейке за последние пять итераций становится меньше числа, указанного в поле Сходимость, поиск прекращается.
Линейная модель - служит для ускорения поиска решения путем применения к задаче оптимизации линейной модели. Нелинейные модели предполагают использование нелинейных функций, фактора роста и экспоненциального сглаживания, что замедляет вычисления.
Неотрицательные значения - позволяет установить нулевую нижнюю границу для тех влияющих ячеек, для которых не было задано соответствующее ограничение в диалоговом окне Добавить ограничение.
Автоматическое масштабирование - используется, когда числа в изменяемых ячейках и в целевой ячейке существенно различаются.
Показывать результаты итераций - приостанавливает поиск решения для просмотра результатов отдельных итераций.
Загрузить модель - после щелчка на этой кнопке отрывается одноименное диалоговое окно, в котором можно ввести ссылку на диапазон ячеек, содержащих модель оптимизации.
Сохранить модель - служит для отображения на экране одноименного диалогового окна, в
котором можно ввести ссылку на диапазон ячеек, предназначенный для хранения модели оптимизации.
Оценка линейная - выберите этот переключатель для работы с линейной моделью.
Оценка квадратичная - выберите этот переключатель для работы с нелинейной моделью.
Разности прямые - используется в большинстве задач, где скорость изменения ограничений относительно невысока. Увеличивает скорость работы средства Поиск решения.
Разности центральные - используется для функций, имеющих разрывную производную. Данный способ требует больше вычислений, однако его применение может быть оправданным, если выдано сообщение о том, что получить более точное решение не удается.
Метод поиска Ньютона - требует больше памяти, но выполняет меньше итераций, чем в методе сопряженных градиентов.
Метод поиска сопряженных градиентов - реализует метод сопряженных градиентов, для которого требуется меньше памяти, но выполняется больше итераций, чем в методе Ньютона. Данный метод следует использовать, если задача достаточно большая и необходимо экономить память или если итерации дают слишком малое отличие в последовательных приближениях.

Решение математических задач в среде Excel

1 Численное дифференцирование

Известно, что численными приближенными методами производная функции в

заданной точке может быть вычислена с использованием конечных разностей.

Выражение, записанное в конечных разностях, для вычисления производной

функции одного переменного имеет вид:

Для вычисления производной в Excel будем использовать приведенную

зависимость.

Рассмотрим методику вычисления производной на примере упражнения.

1.

Допустим требуется найти производную функции Y= 2x3 + x2 в точке x=3.

Производная, вычисленная аналитическим методом, равна 60.

Для вычисления производной выполните следующие действия:

. табулируйте заданную функцию в окрестности точки х=3 с достаточно малым

шагом, например 0,001 (см рис.)

. в ячейку С2 введите формулу вычисления производной. Здесь ячейка В2

содержит значение хк+1, ячейка А2 - хк.

. буксировкой скопируйте формулу до строки 7, получим значения производных

в точках табуляции аргумента.

Для значения х =3 производная функции равна значению 60,019, что близко к

значению, вычисленному аналитически.

2 Численное вычисление определенных интегралов

Для численного вычисления определенного интеграла методом трапеций

используется формула:

Методику вычисления определенного интеграла в Excel с использованием

приведенной формулы рассмотрим на примере.

2.

Пусть требуется вычислить определенный интеграл

Величина интеграла, вычисленная аналитически равна 9. Для численного

вычисления величины интеграла с использованием приведенной формулы

выполните следующие действия:

. табулируйте подинтегральную функцию в диапазоне изменения значений

аргумента 0 – 3 (см. рис.).

. в ячейку С3 введите формулу =(A3-A2)*B2+(A3-A2)*(B3-B2)/2+C2,

которая реализует подинтегральную функцию.

. Скопируйте буксировкой формулу, записанную в ячейке С3 до значения

аргумента х = 3. Вычисленное значение в ячейке С17 и будет

величиной заданного интеграла - 9.

3 Нахождение экстремумов функций с помощью инструмента Поиск решения

Если функция F(x) непрерывна на отрезке [a, b] и имеет внутри этого

отрезка локальный экстремум, то его можно найти используя надстройку Excel

Поиск решения.

Рассмотрим последовательность нахождения экстремума функции на примере

следующего упражнения.

3.

Пусть задана неразрывная функция Y= X2+X +2. Требуется найти ее

экстремум (минимальное значение).

Для решения задачи выполните действия:

. В ячейку А2 рабочего листа введите любое число принадлежащее области

определения функции, в этой ячейке будет находиться значение Х;

. В ячейку В2 введите формулу, определяющую заданную функцию. Вместо

переменной Х в этой формуле должна быть ссылка на ячейку А2: =A2^2 + A2

+2

. Выполните команду меню Сервис/Поиск решения;

. Настройте параметры инструмента Поиск решения: число итераций – 1000,

относительная погрешность 0,00001.

. в поле Установить целевую ячейку укажите адрес ячейки, содержащей формулу

(А2), установите переключатель Минимальному значению, в поле Изменяя

ячейки введите адрес ячейки, содержащей Х (А2);

. Щелкните на кнопке Выполнить. В ячейке А2 будет помещено значение Х

функции, при котором она имеет минимальное значение, а в ячейке В2 –

минимальное значение функции.

Обратите внимание, что в окне Поиск решения можно устанавливать

ограничения. Их целесообразно использовать, если функция

многоэкстремальна, а нужно найти экстремум в заданном диапазоне изменения

аргумента.

4 Решение систем линейных уравнений

1 Встроенные функции для работы с матрицами

В библиотеке Excel в разделе математических функций есть функции для

выполнения операций над матрицами (табл.1.1).

Таблица 1.1

|Русифицированное имя функции|Англоязычное имя |Выполняемое действие |

| |функции | |

|МОБР (параметр) |MINVERSE (parametr) |обращение матрицы |

|МОПР (параметр) |MDETERM (parametr) |вычисление определителя |

| | |матрицы |

|МУМНОЖ (список параметров) |MMULT (parametrlist)|Умножение матриц |

Параметрами функций, приведенных в таблице, могут быть адресные ссылки

на массивы, содержащие значения матриц, или имена диапазонов и выражения,

например

МОБР (А1: B2) или МОПР (матрица_1).

2 Решение систем линейных уравнений

Известно, что система линейных уравнений в матричном представлении

записывается в виде:

AX=B.

Решение такой системы записывается в виде

X=A-1B,

Где A-1 –матрица, обратная по отношению к А.

3 Пример решения системы линейных уравнений:

Пусть система уравнений задана матрицами:

Для решения задачи выполните действия:

. Выделите диапазон размерностью 2 х 2 и присвойте ему имя А;

. Выделите диапазон размерностью 1 х 2 и присвойте ему имя В;

. Выделите диапазон размерностью 1 х 2 и присвойте ему имя Х;

. Используя список имен выделите диапазон А и введите в него значения

элементов матрицы А;

. Используя список имен выделите диапазон В и введите в него значения

элементов вектора В;

. Используя список имен выделите диапазон Х для помещения результата

решения системы;

. В выделенный диапазон Х введите формулу

=МУМНОЖ(МОБР(А);В);

. Укажите Excel, что выполняется операция над массивами, для этого нажмите

комбинацию клавиш ++, в ячейках диапазона Х будет

получен результат: х1=2,16667, х2= - 1,33333

Чтобы выполнить проверку полученных результатов достаточно перемножить

исходную матрицу на вектор результата, итогом этой операции является вектор

свободных членов.

4.

Решите систему уравнений вида AX=B и выполните проверку решения

5 Решение нелинейных уравнений методом подбора параметра

Используя возможности Excel можно находить корни нелинейного уравнения

в допустимой области определения переменной. Последовательность операций

нахождения корней следующая:

1. Уравнение представляется в виде функции одной переменной;

2. Производится табулирование функции в диапазоне вероятного

существования корней;

3. По таблице фиксируются ближайшие приближения к значениям корней;

4. Используя средство Excel Подбор параметра, вычисляются корни

уравнения с заданной точностью.

Рассмотрим последовательность отыскания корней нелинейного уравнения

на примере.

5.

Требуется найти все корни уравнения X3-0,01X2-0,7044X+0,139104=0 на

отрезке [-1; 1]. Правая часть уравнения представлена полиномом третьей

степени, следовательно, уравнение может иметь не более трех корней.

1. представим уравнение в виде функции

Y = X3-0,01X2-0,7044X+0,139104

Известно, что корни исходного уравнения находятся в точках пересечения

графика функции с осью Х.

2. Для локализации начальных приближений необходимо определить интервалы

значений Х, внутри которых значение функции пересекает ось абсцисс, т.е.

функция меняет знак. С этой целью табулируем функцию на отрезке [–1;+1] с

шагом 0,2, получим табличные значения функции. Из полученной таблицы

находим, что значение функции трижды пересекает ось Х, следовательно,

исходное уравнение имеет на заданном отрезке все три корня.

3. Анализ таблицы показывает, что функция меняет знак в следующих

интервалах значений аргумента Х: (-1;-0,8), (-0,2;0,4) и (0,6;0,8).

Поэтому в качестве начальных приближений возьмем значения Х: -0,8; -0,2 и

0,6.

4. На свободном участке рабочего листа, как показано на рисунке, в ячейки

А15: A17 введите начальные приближения, а соответствующие ячейки столбца

В скопируйте формулу.

5. Выполните команду меню Сервис/Параметры, во вкладке Вычисления

установите относительную погрешность вычислений E=0,00001, а число

итераций N=1000, установите флажок Итерации.

6. Выполните команду меню Сервис/Подбор параметра. В диалоговом окне

заполните следующие поля:

Установить в ячейке: в поле указывается адрес ячейки, в которой записана

формула правой части функции;

Значение: в поле указывается значение, которое должен получить полином в

результате вычислений, т.е. правая часть уравнения (в нашем случае 0);

Изменяя значение: в поле указывается адрес ячейки (где записано начальное

приближение), в которой будет вычисляться корень уравнения и на которую

ссылается формула.

После щелчка на ОК получим значение первого корня: -0,92.

Выполняя последовательно операции аналогичные предыдущим, вычислим

значения остальных корней: -0,209991 и 0,720002.

6 Решение систем нелинейных уравнений

Применяя надстройку Excel Поиск решения можно решать системы

нелинейных уравнений. Предварительно система уравнений должна быть

приведена к одному уравнению. Рассмотрим последовательность решения на

примере упражнения.

6.

Дана система двух уравнений:

Требуется найти все корни приведенного уравнения для диапазона значений х и

y [-3; 3].

Шаг 1. Приведем систему к одному уравнению. Пара (x, y) является решением

системы тогда и только тогда, когда она является решением следующего

уравнения с двумя неизвестными:

(x2 + y2 – 3)2 + (2x + 3y – 1)2 = 0

Шаг 2. Для решения последнего уравнения необходимо найти начальные

приближения, для этого табулируем выражение, стоящее в левой части как

функцию по двум переменным x и y. Для табуляции функции выполните следующие

действия:

. В столбец А введите последовательность значений Х с шагом 0,5, а строку 3

– последовательность значений У также с шагом 0,5.

. Присвойте диапазонам значений Х и У имена Х и У, соответственно.

. Выделите диапазон ячеек, в котором будут вычисляться значения функции

(B4:N16).

. В выделенный диапазон введите формулу

=(Х^2+Y^2-3)^2+(2*Х+3*Y-1)^2.

. Нажав комбинацию клавиш [Ctrl]+[Shift]+[Enter] выполните операцию над

выделенным массивом. В выделенном диапазоне появятся вычисленные значения

функции.

Шаг 3. Найдем начальные приближения. Поскольку табулируемая функция задает

поверхность, то начальные приближения следует искать во впадинах, т.е. в

точках, где функция принимает наименьшие значения. На рисунке эти точки

затемнены. Начальными приближениями являются пары (-1;1) и (1,5; -0,5).

Введите значения найденных приближений в смежные ячейки рабочего листа (

см. рис.). Над столбцами сделайте надписи XX и YY, которые будут выполнять

в формулах роль меток. Обратите внимание, что мы уже использовали имена Х и

Y, поэтому имена новых меток должны отличаться.

Шаг 4. В ячейку строки, в которой записана первая пара Х и У введите

формулу, вычисляющую значение функции:

=(XX^2+YY^2-3)^2+(2*XX+3*YY-1)^2

и скопируйте ее в следующую строку.

Шаг 4. Установите курсор на ячейку, в которой записана формула и выполните

команду меню Сервис/Поиск решения. Выполните настройку параметров

инструмента Поиск решения: Предельное число итераций – 1000, относительная

погрешность 0,000001.

В окне Поиск решения в качестве целевой ячейки установите адрес ячейки,

содержащей формулу, взведите переключатель Минимальному значению, в поле

Изменяя ячейки укажите адрес диапазона, содержащего начальные приближения и

щелкните на ОК. В ячейках, где хранились начальные приближения будет

получена первая пара корней.

Повторите такие же операции для второй пары приближений.

Решением системы являются пары (-1,269; 1,1791) и (1,5764; -0,718).

Задания для самостоятельной работы

1. Найти корни уравнения:

|Вариант |Уравнение |Ответ |

|1 |Sin(x)e-2x = 0 для значений х [-2;2] |Х = 0 |

|2 |X3-2,56x2-1,3251x+4,395006=0 |X=-0,94644 |

|3 |X3-2,92x2+1,4355x+0,791136=0 для х |-0,32; 1,229997; |

| |[-3;3] |2,010001 |

|4 |x3-2,84x2-5,6064x-1476336 = 0 |4,700766 |

|5 |X3+1,41x2-5,4724x-7,380384 = 0 |3,542723 |

2. Найти корни линейного уравнения вида Ах=В и выполнить проверку:

Вариант 1 Вариант2

Вариант 3 Вариант 4

3. Найти производную функции:

a) Y = 2x2 при х = 3

b) Y= Sin(x) для х = 0

c) Y = Cos(x) для х = 0

d) Y= Sin(x) для х = Пи/2

e) Y = Cos(x) для х = Пи/2

f) Y= Tg(x) для х = 0

4. Вычислить определенный интеграл:

А) В)

С) D)

5. Найти экстремум функции:

a) Y = (2 – x)2

b) Y = x2 + y2 – 3

c) Y = (x-2)2 +(y+3)2-6

d) Y = sin(2x) для х [0; Пи/2]

Практические задания

Вариант 1

Разбить учебную группу на несколько подгрупп:

Первая группа студентов представляет задачу, излагая основные, решающие факторы, определяющие в главных чертах течение явления, и также вторичные, второстепенные факторы, влияющие на течение явления в качестве «погрешностей». Так прежде чем изложить данную задачу, студентам необходимо всецело осмыслить её и достаточно понятно представить другим участникам игры.

Вторая группа студентов выделяет ключевые моменты задачи и пытается решить её по классической схеме (проводя непосредственно опыты), в некоторых случаях с уменьшая число экпериментов, не используя математических методов и законов теории вероятности. Это позволяет студентам наглядно понять, в чём заключается суть задачи, выявить возможные погрешности эксперимента и определить алгоритм решения задачи посредством математических законов теории вероятностей.

Третья группа студентов пытается представить (с помощью преподавателя) возможные классические парадоксы теории вероятности схожих с предложенной задачей. В результате студентам будут представлены возможные ошибки при решении данной задачи, которые однажды допустили известные учёные, что позволит студентам однозначно определиться с решением задачи.

Четвёртая группа студентов представляет решение задачи с помощью основных математических законов, методов и формул.

Следующую задачу предлагает та группа, которая изложит верное решение задачи, используя математический аппарат, а все остальные группы меняются ролями поочередно. В итоге выигрывает та группа, которая сможет выполнить все роли в результате циркуляции всех рассматриваемых задач.

Тема исследуемых задач может быть объявлена заранее преподавателем (по согласованию со студентами), с целью подготовки студентов к исполнению любой роли. Приведём примеры некоторых из них:

1.С какой вероятностью монета, брошенная дважды, по крайней мере, один раз выпадет гербом?

2.Правильная игральная кость при бросании с равными шансами падает на любую из граней 1, 2, 3, 4, 5, 6. В случае бросания двух костей сумма выпавших чисел заключена между 2 и 12. Как 9, так и 10 из чисел 1, 2, … 6 можно получит двумя способами: 9=3+6=4+5 и 10=4+6=5+5. В задаче с тремя костями и 9, и 10 получаются шестью способами. Почему тогда 9 появляется чаще, когда бросают две кости, а 10, когда бросают три?

3. Шесть шаров случайным образом раскладывают в три ящика. Найти вероятность того, что во всех ящиках окажется разное число шаров, при условии, что все ящики не пустые.

4. Устройство, состоящее из пяти независимо работающих элементов, включается за время Т. Вероятность отказа каждого из них за это время равна 0,2. Найти вероятность того, что откажут:

а) три элемента;

б) не менее четырех элементов;

в) хотя бы один элемент.

5. Имеется 3 ящика, в первом из которых 6 стандартных и 3 бракованных детали, во втором- 5 стандартных и 4 бракованных и в третьем 7 стандартных и 4 бракованных. Найти вероятность того, что если из каждого ящика выбрать по детали, то среди них будет одна стандартная и две бракованных.

После нескольких занятий студентам можно предложить придумывать условия задач самим.

Вариант 2

МОДЕЛИРОВАНИЕ ЭКОНОМИКИ И МЕНЕДЖМЕНТА

Компьютерная деловая игра МЭКОМ (Моделирование ЭКОномики и Менеджмента) известна в России с 1991 года.

Ядром игры является американская программа Management and Economic Simulation Exercise (MESE), созданная по заказу американской образовательной корпорации Junior Achievement (JA) более 10 лет назад Гарвардским университетом. Создателем программы является Bill Glass. Американская образовательная корпорация JA существует не один десяток лет и создала целый ряд очень удачных технологий для обучения школьников экономике. Одной их таких технологий и является МЭМ. Математическая модель, заложенная в данную программу, настолько удачно соотносит существенное и несущественное в рыночных отношениях, что, видимо, это и является ее пропуском в образовательные программы многих стран мира.

Соревнования по МЭКОМ долгое время входили в программы олимпиад по экономике различного уровня, а также до сих пор турниры МЭКОМ проводятся в сети Интернет. Автором компьютерной версии программы МЭКОМ в России является Международный Центр Экономического и Бизнес Образования (МЦЭБО).

В Европе в 2009 году коллеги при финансовой поддержке EUREL проводили международный турнир International Management Cup 2009 среди студентов электротехнических специальностей вузов Польши, Швеции, Швейцарии, Италии, Австрии и Германии на основе похожей симуляционной деловой игры, применяемой в тренингах менеджеров в компании Siemens, финальный этап игры состоялся в сентябре 2009 года в Венеции.

Дата добавления: 2015-06-26