Используемые информационные и педагогические технологии 2 страница

Стоимость 3-его плана:

D₃=1•35+2•15+0,4•5+1•15+0,8•40+1•35+1,5•35+2,5•40=301,5.

Имеем:u₁+v₆-c₁₆ =0,3>0,u₃+v₅-c₃₅ =0,3>0. => По критерию оптимальности, третий план не оптимален. Далее max(0,3;0,3)=0,3. => Поместим перевозку в клетку А₃В₅, сместив 40=min(40,40) по циклу, указанному в таблице штрихом. Получим новую таблицу. Чтобы 4-ый план был невырожденным, оставим в клетке А₄В₅ нулевую перевозку. Найдем потенциалы: u₁+v₁=1,u₁+v₂=2,u₂+v₁=0,4,u₃+v₂=1, u₄+v₅=2,5, u₂+v₃=1, u₄+v₄=1,5, u₃+v₅=1,5, u₄+v₆=0. Положим u₁=0,тогда v₁=1,u₂=-0,6,v₂=2,v₄=1,5, u₃=-1,u₄=0, v₃=1,6, v₅=2,5, v₆=0. Составим таблицу 3.:

Таблица 3. - Проведение итераций

Цеха   Склад	B1 (b1=40) v1=1	B2 (b2=50) v2=2	B3 (b3=15) v3=1,6	B4 (b4=75) v4=1,5	B5 (b5=40) v5=2,5	B6 (b6=5) v6=0
А1 (а1=50) U1=0	1,0	- 1,4 2,0	- 1 3,0	- 1 2,5	3,5
А2(а2=20) U2=-0,6	- 1,6 0,4	3,0	- 1,1 1,0	- 1,1 2,0	- 0,6 3,0
-0,7 А3(а3=75) U3=-1	0,7	-0,4 1,0	-0,3 1,0	0,8	- 1 1,5
-0,2 А4(а4=80) U4=0	1,2	-0,4 2,0	2,0	1,5	2,5	0

Стоимость 4-ого плана:

D₄=1•35+2•15+0,4•5+1•15+1•35+1,5•40+1,5•75=289,5.

Для всех клеток последней таблицы выполнены условия оптимальности:

1) u_i+v_j-с_ij=0 для клеток, занятых перевозками;

2) u_i+v_j-с_ij ≤0 для свободных клеток.

Несодержательные ответы:

Прямой ЗЛП:

35 15 0 0 0 0

5 0 15 0 0 0

X = 0 35 0 0 40 0

0 0 0 75 0 5

min=289,5.

Двойственной ЗЛП:

U₁=0; U₂=-0,6; U₃=-1; U₄=0; V₁=1; V₂=2; V₃=1,6; V₄=1,5; V₅=2,5; V₆=0.

max=289,5.

Так как min=max, то по критерию оптимальности найдены оптимальные решения прямой и двойственной ЗЛП. Содержательный ответ: Оптимально перевозить так:

Из А₁ в B₁ – 35 сборочных агрегатов;

Из А₁ в B₂ – 15 сборочных агрегатов;

Из А₂ в B₁ – 5 сборочных агрегатов;

Из А₂ в B₃ – 15 сборочных агрегатов;

Из А₃ в B₂ – 35 сборочных агрегатов;

Из А₃ в B₅ – 40 сборочных агрегатов;

Из А₄ в B₄ – 75 сборочных агрегатов.

При этом стоимость минимальна и составит D_min=289,5. 5 сборочных агрегатов необходимо оставить на складе А₄ для их последующей перевозки в другие Цеха.

Глоссарий

Игра называется бесконечной, если у каждого игрока имеется бесконечное число стратегий.

Вершины, прилегающие к одному и тому же ребру, называются смежными.

Вырожденный опорный план - опорный план, число ненулевых компонент которого меньше числа ограничений.

Геометрическое программирование. Под задачами геометрического программирования понимают задачи наиболее плотного расположения некоторых объектов в заданной двумерной или трехмерной области. Такие задачи встречаются в задачах раскроя материала для производства каких-то изделий и т.п. Это - еще недостаточно разработанная область математического программирования и имеющиеся здесь алгоритмы в основном ориентированы на сокращение перебора вариантов с поиском локальных минимумов.

Геометрическое решение игры - нахождение решения игры посредством представления данных задачи в виде геометрических фигур на координатной плоскости.

Граф это множество точек или вершин и множество линий или ребер, соединяющих между собой все или часть этих точек.

Дерево это связный граф без циклов.

Динамическое программирование. Для отыскания оптимального решения планируемая операция разбивается на ряд шагов (этапов) и планирование осуществляется последовательно от этапа к этапу. Однако выбор метода решения на каждом этапе производится с учетом интересов операции в целом.

Задачами теории массового обслуживания является анализ и исследование явлений, возникающих в системах обслуживания. Одна из основных задач теории заключается в определении таких характеристик системы, которые обеспечивают заданное качество функционирования, например, минимум времени ожидания, минимум средней длины очереди.

Игра - математическая модель конфликтной ситуации, стороны, участвующие в конфликте, называются игроками, а исход конфликта - выигрышем.

Канонической форма задачи ЛП является задачей на максимум (минимум) некоторой линейной функции F, ее система ограничений состоит только из равенств (уравнений). При этом переменные задачи х₁, х₂ ,..., х_n являются неотрицательными.

Компьютерная модель — это модель, реализованная средствами программной среды.

Игра называется конечной, если у каждого игрока имеется конечное число стратегий.

Граф без цикла называется лесом.

Линейное программирование состоит в нахождении экстремального значения линейной функции многих переменных при наличии линейных ограничений, связывающих эти переменные.

Вершины степени 1 в дереве называются листьями.

Личный ход — это сознательный выбор игроком одного из возможных действий.

Максиминная стратегия - стратегия игрока, при которой он стремится сделать минимальный выигрыш максимальным, т. е. получить наилучшую выгоду в наихудших условиях.

Математическая модель любой задачи линейного программирования включает в себя:

максимум или минимум целевой функции (критерий оптимальности);

систему ограничений в форме линейных уравнений и неравенств;

требование неотрицательности переменных.

Математические моделирование – наука, занимающаяся разработкой и практическим применением методов наиболее оптимального управления организационными системами.

Матричные игры - это игры, математические модели которых можно представить в виде матриц.

Модель – материальный или мысленно представляемый объект, который в процессе исследования замещает объект-оригинал так, что его непосредственное изучение дает новые знания об объекте-оригинале.

Моделировaние – это изучение объектa путем построения и исследования его модели, осуществляемое с определенной целью и состоит в зaмене экспериментa с оригинaлом экспериментом нa модели.

Метод аппроксимации Фогеля - один из группы методов определения первоначального опорного плана транспортной задачи. Данный метод состоит в следующем:

на каждой итерации находят разности между двумя наименьшими тарифами во всех строках и столбцах, записывая их в дополнительные столбец и строку таблицы;

находят max Δc_ij и заполняют клетку с минимальной стоимостью в строке (столбце), которой соответствует данная разность.

Метод двойного предпочтения - один из группы методов определения первоначального опорного плана транспортной задачи.

Метод минимальной стоимости - один из группы методов определения первоначального опорного плана транспортной задачи. Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую, и в клетку, которая ей соответствует, помещают меньшее из чисел a_i , или b_j.

Метод потенциалов - один из методов проверки опорного плана транспортной задачи на оптимальность.

Метод северо-западного угла - один из группы методов определения первоначального опорного плана транспортной задачи.

Минимаксная стратегия - стратегия игрока, при которой он стремится сделать максимальный проигрыш минимальным.

Игра называется множественной, если число игроков больше двух.

Нелинейное программирование. Целевая функция и ограничения могут быть нелинейными функциями.

Игра с нулевой суммой (антагонистическая), если выигрыш одного из игроков равен проигрышу другого.

Оптимальный план ЗЛП - решение задачи линейного программирования, т. е. такой план, который входит в допустимую область и доставляет экстремум целевой функции.

Остовной подграф - это граф, множество вершин которого совпадает с множеством вершин самого графа.

Открытая ТЗ - если общее количество груза в пунктах отправления и общая потребность в пунктах назначения не совпадают ()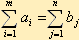

Игра называется парной, если в ней участвуют два игрока.

Подграф графа - это граф, являющийся подмоделью исходного графа, т. е. подграф содержит некоторые вершины исходного графа и некоторые ребра (только те, оба конца которых входят в подграф).

Полным называется граф, в котором каждые две вершины смежные.

Платежная матрица игры - матрица размерности m на n, i = 1,..., n, j = 1,..., m, (i,j)-ый элемент которой значение выигрыша (пригрыша) игроков в случае i-го хода первого игрока и j-го хода второго игрока.

Предмет теории игр принятие решений в условиях неопределенности, в условиях столкновения, конфликтных ситуациях, когда принимающий решение субъект (игрок), располагает информацией лишь о множестве возможных ситуаций, в одной из которых он в действительности находится, о множестве решений, которые он может принять, и о количественной мере того выигрыша, который он мог бы получить, выбрав в данной ситуации данную стратегию.

Принцип оптимальности динамического программирования - каково бы ни было состояние системы в результате какого-либо числа шагов, на ближайшем шаге нужно выбирать управление так, чтобы оно в совокупности с оптимальным управлением на всех последующих шагах приводило к оптимальному выигрышу на всех оставшихся шагах, включая выигрыш на данном шаге. Простая цепь - маршрут, в котором все вершины попарно различны.

Простой граф - это граф без кратных ребер и петель.

Простой цикл - цикл, в котором все вершины, кроме первой и последней, попарно различны.

Пустым называется граф без ребер.

Путь в ориентированном графе это последовательность дуг, в которой конечная вершина всякой дуги, отличной от последней, является начальной вершиной следующей.

Решение – всякий определенный набор зависящих параметров.

Граф называется связным, если любая пара его вершин связана.

Симплекс метод - алгоритм последовательного улучшения плана, позволяющий осуществлять переход от одного допустимого базисного решения к другому таким образом, что значение целевой функции непрерывно возрастают и за конечное число шагов находится оптимальное решение.

Седловой точкой действительной функции f (x,y), определённой для всех x € A, y € B, называется точка (x₀ , y₀ ), где x € A, y € B, если выполнены следующие условия:

x € A, f (x, y₀x,y0) f (x₀ , y₀),

x € В, f (x₀ , y₀) f (x₀ , y).

Случайный ход — это случайно выбранное действие игроком.

Стандартная форма задачи линейного программирования является задачей на максимум (минимум) линейной целевой функции. Система ограничений ее состоит из одних линейных неравенств типа «≤» или «≥». Все переменные задачи неотрицательны.

Стационарная точка - точка X*, в которой все частные производные функции Z = f (Х) равны 0.

Степень вершины - это удвоенное количество петель, находящихся у этой вершины плюс количество остальных прилегающих к ней ребер.

Стохастическое линейное программирование. Бывает много практических ситуаций, когда коэффициенты c_i целевой функции, коэффициенты a_ij в матрице коэффициентов, коэффициенты ограничений b_i - являются случайными величинами. В этом случае сама целевая функция становится случайной величиной, и ограничения типа неравенств могут выполняться лишь с некоторой вероятностью. Приходится менять постановку самих задач с учётом этих эффектов и разрабатывать совершенно новые методы их решения. Соответствующий раздел получил название стохастического программирования.

Стратегией игрока называется совокупность правил, определяющих выбор его действия при каждом личном ходе в зависимости от сложившейся ситуации.

Теорема об активных стратегиях. Если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш остается неизменным и равным цене игры v, если второй игрок не выходит за пределы своих активных стратегий.

Теория графов. С помощью теории графов решаются многие сетевые задачи, связанные с минимальным протяжением сети, построение кольцевого маршрута и т.д.

Теория игр пытается математически объяснить явления возникающие в конфликтных ситуациях, в условиях столкновения сторон. Такие ситуации изучаются психологией, политологией, социологией, экономикой.

Транспортная задача - в общем виде состоит в определении оптимального плана перевозок некоторого однородного груза из m пунктов отправления A₁, A₂ ,..., A_m в n пунктов назначения B₁, B₂ ,..., B_n.

Ход игрока - выбор и осуществление одного из предусмотренных правилами действий.

Целевая функция - функция в математическом программировании, для которой требуется найти экстремум.

Цена игры - величина выигрыша игрока.

Выигрыш, соответствующий оптимальному решению, называется ценой игры v.

Цепь маршрут, в котором все ребра попарно различны.

Цикл замкнутый маршрут, являющийся цепью.

Циклом называют замкнутую ломаную линию, все вершины которой лежат в занятых ячейках, кроме одной, расположенной в свободной клетке, подлежащей заполнению, а звенья параллельны строкам и столбцам, причем в каждой строке (столбце) лежит не более 2 -х вершин.

Чистые стратегии - возможные ходы в распоряжении игроков.

Элементы решения – параметры, совокупность которых образует решение

Антиградиент – (в линейном программировании) вектор, равный градиенту с обратным знаком и показывающий направление убывания целевой функции.

Градиент – (в линейном программировании) вектор, составленный из коэффициентов целевой функции и показывающий направление ее возрастания.

Графический метод – метод решения задачи линейного программирования, заданной на плоскости, т.е. содержащей только две переменные.

Двухфазный симплекс-метод – одна из модификаций симплекс-метода, применяющая искусственные переменные.

Доминирование – (в матричных играх) процесс исключения из рассмотрения заведомо "слабых" стратегий.

Задача линейного программирования – экстремальная задача, в которой целевая функция и ограничения задаются линейными соотношениями.

Задача принятия оптимального решения – проблема, в которой требуется найти наилучший (в том или ином смысле) способ достижения поставленной цели.

Значение (цена) игры – (в матричных играх) числовое значение выигрыша первого игрока, соответствующее седловой точке.

Игра – (здесь) математическая модель проблемы конфликтного принятия решения.

Искусственные переменные – (в линейном программировании) вспомогательные переменные, применяемые для построения начального допустимого базисного решения в задаче линейного программирования.

Исследование операций (ИО) – раздел прикладной математики, занимающийся математическими моделямизадач принятия оптимальных решений и их применениями.

Каноническая форма – (в линейном программировании) задача линейного программирования, в которой все ограничения имеют вид строгих равенств, а их правая часть (свободные члены) неотрицательна.

Конфликтная задача принятия решения – проблема, в которой требуется найти наилучшие решения для сторон (лиц) с учетом пересечения их интересов.

Линия уровня (целевой функции) – (в линейном программировании) прямая линия, в каждой точке которой целевая функция принимает одно и то же числовое значение.

Математическая модель – формальная схема реального объекта (процесса, проблемы), составленная с помощью математических обозначений, символов и соотношений.

Математическое программирование (МП) – раздел методов оптимизации, занимающийся исследованием оптимизационных задач с ограничениями в виде неравенств и уравнений.

Матричная игра – антагонистическая игра, в которой каждый игрок (лицо, принимающее решение) имеет лишь конечное число стратегий (решений).

Метод потенциалов – метод решения транспортной задачи.

Метод северо-западного угла – метод вычисления начального опорного плана в транспортной задаче (имеются также "метод минимальной стоимости", "метод двойного предпочтения" и др.).

Методы оптимизации – раздел прикладной математики, занимающийся исследованием экстремальных задач.

Неопределенность – (здесь) ситуация, когда приходится принимать решение в условиях отсутствия информации.

Ограничения – математические соотношения (элемент экстремальной задачи), отражающие условия, накладываемые на аргументы целевой функции.

Опорный план – (в транспортной задаче) план перевозок, у которого число ненулевых перевозок равно сумме числа производителей и потребителей без единицы.

Потенциалы – вспомогательные переменные в транспортной задаче, вводимые для проверки оптимальности плана перевозок.

Прикладная математика – раздел математической науки, занимающийся вопросами применения математических подходов и методов в разных сферах человеческой деятельности.

Седловая точка – (в матричных играх) пара, составленная из оптимальных стратегий игроков.

Симплекс-метод – общий и универсальный метод решения задачи линейного программирования.

Слабые переменные – (в линейном программировании) вспомогательные переменные, применяемые для получения канонической формызадачи линейного программирования.

Смешанная стратегия – (в матричных играх) вероятностное распределение на множестве чистых стратегий, т.е. вектор, компонентами которого являются вероятности выбора чистых стратегий.

Теория игр – раздел исследования операций, занимающийся математическими моделямизадач принятия оптимальных решений в условиях конфликта и неопределенности.

Точка максимума (минимума) – (в математическом программировании) конкретное числовое значение вектора, составленного из аргументов целевой функции, которому соответствует наибольшее (наименьшее) значение целевой функции.

Транспортная задача – математическая модель проблемы составления наилучшего (в том или ином смысле) плана перевозок товара от производителей к потребителям.

Формализация – (здесь) составление математической модели реальной проблемы.

Целевая функция – математическая функция (элемент экстремальной задачи), отражающая цель принятия решения.

Экстремальная (оптимизационная) задача – математическая задача, в которой требуется найти максимальное или минимальное значение заданной функции с учетом существующих на ее аргументы ограничений.

Вопросы для текущего контроля:

Модуль 1 «Математические методы в экономике»

13. Матрицы и действия над матрицами.

14. Решение систем линейных уравнений.

15. Векторы и действия с векторами.

16. Модель межотраслевого баланса и модель международной торговли.

17. Общая задача линейного программирования и составление моделей задач математического программирования.

18. Графический метод решения задачи линейного программирования.

19. Симплексный метод решения задачи линейного программирования.

20. Двойственные задачи линейного программирования.

21. Корреляция, вычисление коэффициентов корреляции.

22. Линейная модель парной регрессии.

23. Модель множественной регрессии.

24. Анализ временных радов экономических процессов.

Модуль 2 «Современные компьютерные технологии в экономике»

15. Информационные технологии документального обеспечения управленческой деятельности.

16. Технологии обработки экономической информации на основе использования систем управления базами данных.

17. Сетевые технологии и системы распределенной обработки информации, вычислительные сети.

18. Архитектура файл-сервер, клиент-сервер.

19. Коммуникационное оборудование сетей и методы коммуникаций.

20. Технологии поддержки принятия решений. Технологии контроля исполнения.

21. Информационно-поисковые технологии. Технологии хранилищ данных.

22. Правовые информационные технологии.

23. Технологии работы с персоналом.

24. Экспертные технологии.

25. Комплексные системы информационной поддержки управления.

26. Выбор и внедрение систем информационного обслуживания на предприятиях (в организациях).

27. Компьютерные технологии интеллектуальной поддержки управленческих решений.

28. Системы электронной коммерции.

Вопросы для подготовки к зачету:

27. Матрицы и действия над матрицами.

28. Решение систем линейных уравнений.

29. Векторы и действия с векторами.

30. Модель межотраслевого баланса и модель международной торговли.

31. Общая задача линейного программирования и составление моделей задач математического программирования.

Дата добавления: 2015-06-26