Вопрос № 5 Дайте обоснование векторной формулы момента силы относительно точки

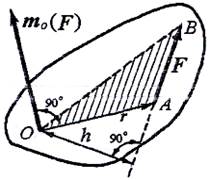Пусть даны сила F, приложенная в точке А тела, и некоторый центр О. Вращательный эффект силы F относительно точки О зависит от модуля силы F и кратчайшего расстояния h от точки О до линии дей­ствия силы. Это кратчайшее расстояние h называется плечом силы от­носительно данной точки (рис. 1.13). Кро­ме того, вращательный эффект силы зави­сит от положения в пространстве плоско­сти поворота треугольника ОАВ, проходя­щей через моментную точку О и линию действия силы F, и от направления пово­рота в этой плоскости. Для количественно­го измерения вращательного эффекта силы F, относительно заданной точки, введем понятие момента силы. Моментом силы относительно точки называется алгебраиче­ская величина, равная произведению модуля силы на кратчайшее рас­стояние от точки до линии действия силы.

Численное значение момента силы F относительно точки О бу­дем обозначать m_o(F). Тогда

mo(F) = ±Fh. (1)

Условились считать момент силы относительно точки положи­тельным, если сила стремится вращать тело вокруг заданного центра против хода часовой стрелки, и отрицательным — по часовой стрелке (рис. 1.14). Из опреде­ления величины момента силы относительно точки следует, что он не зависит от переноса силы вдоль линии ее действия и равен нулю, если линия действия силы проходит через моментную точку.

Геометрически численное значение момента силы F относи­тельно точки О выражается удвоенной площадью треугольника ОАB, вершиной которого является данная точка О, а основанием - сила F:

Момент силы относительно точки О можно принимать за ал­гебраическую величину лишь в случае плоской системы сил. Для про­странственной системы сил определение момента необходимо обобщить так, чтобы в определение этого понятия входило задание положения в пространстве плоскости, проходящей через линию силы и моментную точку. Это можно сделать, если момент силы относительно точки счи­тать вектором, приложенным в этой точке и равным по модулю произ­ведению величины силы на ее плечо. При этом вектор-момент силы должен быть направлен перпендикулярно к плоскости, в которой лежат сила и моментная точка, в ту сторону, откуда вращение тела силой пред­ставляется происходящим против хода часовой стрелки.

Обозначим вектор-момент силы F относительно точки О сим­волом mo(F). Тогда, рассматривая его величину, определяемую форму­лами (1)-(2), и принимая во внимание направление вектор-момента, приходим к заключению, что вектор-момент m0(F) можно определить с помощью следующего векторного произведения:

Итак, момент силы относительно некоторого центра равен векторному произведению радиус-вектора точки приложения силы на
вектор силы.

Дата добавления: 2015-06-04