Вопрос № 11 Дайте определение пары сил и обоснование определения момента пары. Вектор-момент пары и его направление

Система двух равных по величине, антипараллелъных и не лежащих на одной прямой сил (F1 F2), называется парой сил.

Плоскость, в которой расположена пара сил, называется плос­костью действия пары. Кратчайшее расстояние d между линиями дей­ствия сил пары называется плечом пары. Совокупность нескольких пар, действующих на тело, называется системой пар.

Пара сил не имеет равнодействующей, т.е. не может быть заменена одной эквивалентной ей силой. Докажем это исходя от противного. Допустим теперь, что данная пара сил (F1, F2) имеет равнодействующую R, не параллельную силам пары (рис. 1.22). Тогда, добавив к системе сил (F1, F2) уравновешивающую R*", мы получили бы систему трех сил (F1 F2, R**), находящихся в рав­новесии. Но этого не может быть, так как по теореме о трех силах линии действия этих сил должны пересекаться в одной точке, что невозможно. Так как силы, составляющие пару, не находятся в равновесии, не имеют равнодействующей и не могут быть уравновешены одной силой, то пара сил занимает особое место. Непосредственный опыт показывает, что пара сил, приложенная к твердому телу, способна привести его во вращательное движение, если этому не препятствуют наложенные на тело связи. Вращательное дейст­вие пары на тело будет тем больше, чем больше плечо пары и модули сил, образующих пару, и измеряется моментом пары. Численное значение момента пары равно произведению величи­ны одной из сил г.ары на плечо этой пары Условились считать положительным момент такой пары, кото­рая стремится повернуть тело против вращения часовой стрелки, и от­рицательным - момент пары, которая стремится повернуть тело по на­правлению вращения часовой стрелки (рис. 1.23). Тогда алгебраическая величина момента пары (F1 F2) может быть записана так:

M (F1,F2)=+-F1d=F2d

Очевидно, что момент пары равен моменту одной из ее сил от­носительно точки приложения другой. Кроме направления вращения и числового значения момента действие пары на тело, а следовательно, и ее момент зависят от того, как расположена плоскость действия пары, поэтому момент пары обладает определенным направлением в пространстве и, следовательно, есть ве­личина векторная.

Так как направление плоскости в пространстве определяется направлением прямой, перпендикулярной к этой плоскости, то вектор, изображающий момент пары, направляют перпендикулярно плоскости действия пары. . Сторона, в которую направлен вектор-момент пары, должна характеризовать направление вращения пары (рис. 1.24).

Итак, момент пары есть вектор, перпендикулярный к плоско­сти действия пары, направленный в ту сторону, откуда поворот тела данной парой виден происходящим против хода часовой стрелки. Легко видеть, что момент пары численно равен площади парал­лелограмма, построенного на силах пары (рис. 1.25, а). Следовательно, вектор-момент пары равен векторному произведению векторов AB и F,

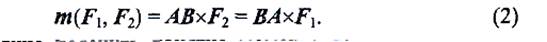
Чтобы лучше пояснить понятие момента пары сил, докажем следующую теорему.

Сумма моментов сил пары относительно любого центра равна моменту пары.

В самом деле, возьмем произвольный центр О и проведем из него радиус-векторы гх и г2 в точки А и. В, где приложены силы пары (F1 F2) (рис. 1.25, б). Тогда

что и требовалось доказать.

Понятие момента пары можно было бы определить как сумму моментов сил пары относительно некоторой точки. Из доказанной тео­ремы следует, что эта сумма не зависит от выбора точки и совпадает с введенным выше определением момента пары.

Вопрос о точке приложения вектор-момента рассмотрен ниже.

Дата добавления: 2015-06-04