Вопрос № 14Сформулируйте и докажите теорему об изменении плеча и сил пары

Теорема 3. Действие пары на абсолютно твердое тело не из­менится, если любым способом видоизменить модули сил и плечо пары, сохраняя постоянным их произведение, т.е. момент пары.

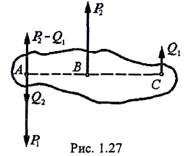Пусть мы имеем пару (Р1 Р2) (рис. 1.27). Разложим силу Р2 на две параллельные силы Q1 и (P1-Q1), приложенные в точках А я С. Силы (P2-Q1) и P1 имеют равно­действующую Q2, модуль которой

Q2=Pl-(P2-Ql) = Ql. В результате мы получили новую пару (Q1 Q2), плечо которой равно A С, причем величина силы Q2 и плечо АС удовле­творяют следующему соотношению:

Последнее равенство означает, что момент данной пары (P1 P2) равен моменту пары (Q1 Q2). Таким образом, теорема доказана.

Вопрос № 15 Сформулируйте и докажите теорему о сложении пар как угодно расположенных в пространстве Теорема 4, Система пар, действующих на абсолютно твердое тело, эквивалентна одной паре, вектор-момент которой равен гео­метрической сумме моментов слагаемых пар.Рассмотрим сначала сложение двух пар, лежащих в пересекаю­щихся плоскостях П1 и П2 (рис. 1.28). Приведем эти пары к общему плечу АВ, лежащему на линии пересечения этих плоскостей. В результате по­лучим две пары (F1 F2) и (Р1 Р2).

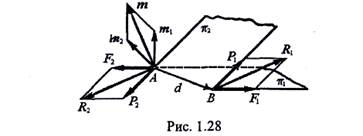Сложив далее силы F1 и Р1 а затем F2 и Р2 получим результи­рующую пару (R1 –R2). т-е- первая половина теоремы доказана. Найдем теперь момент этой результирующей пары:

но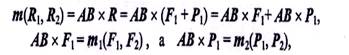

поэтому окончательно получим m(R1,R2)=m1(F1,F2)+m2(P1,P2), (1)

т.е. момент результирующей пары по величине и направлению опреде­ляется диагональю параллелограмма, построенного на вектор-моментах слагаемых пар, т.е. равен их геометрической сумме. Если на тело действует N пар, то, складывая их, последова­тельно применяя доказанную теоре­му, мы установим, что система пар эквивалентна равнодействующей паре с вектор-моментом

(2)

Геометрически момент равнодействующей пары определяется как замыкающая сторона векторного многоугольника. Очевидно, что для равновесия этих пар необходимо и достаточно, чтобы вектор-момент этой равнодействующей был бы равен нулю, т.е.

(3)

Геометрически последнее равенство означает, что векторный много­угольник, построенный на вектор-моментах составляющих пар, замкнут.

Отсюда получаем аналитическое условие равновесия системы пар в сле­дующей форме:

Т.е. для равновесия системы пар, приложенных к твердому те­лу, необходимо и достаточно, чтобы алгебраическая сумма проекций векторов-моментов всех пар системы на каждую из трех координат­ных осей равнялась нулю.

Дата добавления: 2015-06-04