Вопрос № 17 Сформулируйте и докажите теорему о приведении произвольной пространственной системы сил к главному вектору и главному моменту

Вопрос № 16 Сформулируйте и докажите лемму о параллельном переносе силы

Всякая сила, приложенная к абсолютно твердому телу в данной точке А, эквивалентна той же силе, приложенной в любой другой точке В и паре сил, момент которой равен моменту данной силы относительно новой точки приложения.

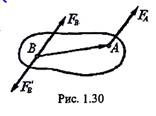Пусть к точке А твердого тела при­ложена сила F_A. Приложим к произвольно выбранной точке В две уравновешенные силы F_B и F'_B, которые равны по величине силе F_A и лежат на линии, параллельной ей (рис. 1.30). Тогда, согласно второй аксиоме, получившаяся система трех сил FA, FB, F'B

эквивалентна данной силе, т.е. (FA, FB, F'B) ~ FA, но силы FA и F'B со­ставляют пару сил, поэтому

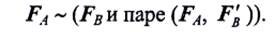
Эта лемма показывает, что данную силу можно переносить па­раллельно самой себе в любую точку тела, присоединив при этом соот­ветствующую пару. Пару, получающуюся при переносе силы з другую точку приложения, называют присоединенной парой. Её момент равен моменту данной силы FA относительно ее новой точки приложения В.

Пусть на твердое тело действует произвольная пространствен­ная система сил (F1 F2,....FN). Выберем произвольный центр О, назы­ваемый центром приведения, и перенесем все силы данной системы в этот центр. В результате получим N сил, приложенных в центре приведения, и N присоединенных пар, т.е. N вектор-моментов присоединенных пар (рис. 1.31, а). Складывая все си­лы, приложенные 2 центре О, получим одну результирующую силу

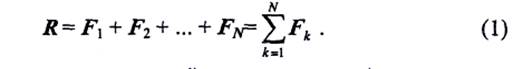
Сила R, равная геом сумме всех сил данной системы, называется главным вектором.

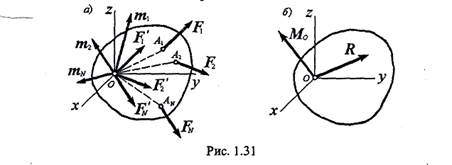
Здесь следует подчеркнуть, что вектор R есть главный вектор данной системы сил (F1 F2,....FN), а не равнод этой системы, так как главный вектор не эквивалентен исходной системе сил. Главный вектор R является равнодействующей системы сил (F’l, F’2,....F'N), а не заданной системы (F1 F2,....FN) (рис. 1. 31, а). Далее на основании теоремы 4 о сложении пар складываем мо­менты присоединенных пар, помня при этом, что момент каждой при­соединенной пары равен моменту исходной силы относительно центра приведения. В результате получим

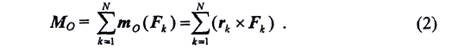Величина Mo равная геометрической сумме моментов всех сил

системы относительно центра приведения, называется главным моментом относительно этого центрам Таким образом, мы доказали сле­дующую теорему: произвольная пространственная система сил, действующих на абсолютно твердое тело, в общем случае эквивалентна одной силе, равной главному вектору этой системы и приложенной в про­извольно выбранном центре приведения О, и главному моменту отно­сительно этого центра приведения (рис. 1.31, б).
Из этой теоремы следует, что две произвольные пространствен­
ные системы сил, имеющие одинаковые главные векторы и главные мо­менты относительно одного центра приведения, эквивалентны.

Дата добавления: 2015-06-04