Момент силы относительно точки

Момент силы относительно точки и оси.

Силы, действующие на свободное твёрдое тело, могут вызвать как поступательное его смещение (сдвиг), так и поворот. Вращательный эффект действия силы количественно оценивается моментом силы относительно точки или относительно оси.

Момент силы относительно точки определим как векторное произведение

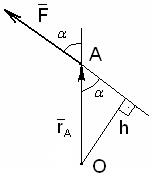
; (1)

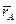- радиус- вектор точки приложения силы, Рис.14;

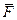- вектор силы.

Обсудим формулу (1), и убедимся в том, что она отвечает нашим интуитивным представлениям о вращательном эффекте действия силы на тело.

Модуль вектора равен

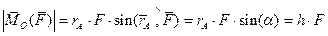. (2)

Величина 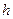называется плечом силы. Из (2) следует, что чем Рис.14. К определению момента силы 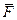относительно точки больше сила, тем больше её момент, что интуитивно понятно. Для уяснения влияния плеча 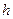, рассмотрим Рис.15, на которомизображён случай, когда сила приложенак гаечному ключу под углом . Ясно, что чем больше плечо 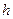силы 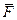, тем большим будет её момент относительно точки О, приложенный

к головке болта. Следовательно, формула (2) правильно количественно определяет

величину вращательного Рис.15. Момент силы 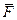, перпендикулярной гаечному ключу

действия силы относительно точки. Осталось понять, почему момент силы относительно точки вводится как величина векторная.

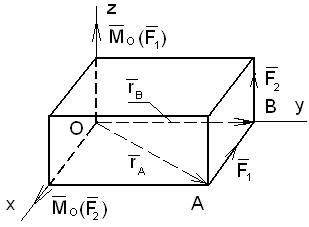В общем случае силы, действующие на тело, стремятся повернуть его вокруг некоторого центра в разных плоскостях. На Рис.16

на твёрдое тело в форме прямоугольного параллелепипеда действуют две силы и 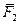. Видно, что сила стремится повернуть тело вокруг точки О в плоскости , а сила 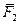стремится повернуть его вокруг того же центра в плоскости 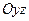. Вектор момента 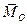, определённый формулой (1), перпендикулярен

Рис.16. Вектор момента силы как плоскости, в которой сила стремится

указатель плоскости поворота тела повернуть тело, и направлен так, чтобы при взгляде с его конца, поворот тела под действием силы был виден происходящим против хода часовой стрелки. Тем самым вектор 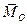указывает ориентацию плоскости, в которой сила стремится повернуть тело. Вот почему момент силы относительно центра должен определяться как величина векторная.

Упражнение 4.1.

Убедитесь в том, что вектор момента (1) не изменится, если сила будет

приложен в любой другой точке на линии действия силы.

Если силы, действующие на тело, расположены в одной плоскости, например, в плоскости , то векторы моментов этих сил относительно точки, лежащей в той же плоскости, будут либо совпадать с положительным направлением оси Oz, Рис. 17,

перпендикулярной плоскости , либо будут иметь противоположное направление.

В этом случае можно различать Рис.17. Моменты относительно точки эти два возможных направления сил, расположенных в одной плоскости

вектора момента с помощью знака. Для этого определим момент силы относительно точки как алгебраическую величину:

, (3)

в которой = 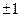. Можно заранее условиться выбирать здесь знак плюс, если при

взгляде со стороны положительного направления оси Oz силастремится повернуть тело против хода часовойстрелки, и выбирать знак минус при стремлении силы повернуть тело по ходу часовой стрелки.

Дата добавления: 2015-06-04