Момент силы относительно оси

Упражнения 4.2.

1. Разложите силу 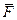на Рис.14 на две составляющих, одна из которых направлена вдоль радиус- вектора 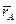, а другая - перпендикулярна ему, и получите формулу (2) для модуля момента силы 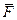относительно точки O.

2. Векторы 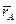и 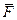в формуле (1) – полярные. К какому типу векторов относится вектор ?

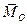Разложим момент силы (1) на составляющие по осям некоторой декартовой системы координат с началом в точке О. Для этого представим вектор

в виде

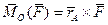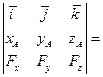
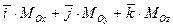= . (1)

Здесь 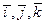- орты осей Ox, Oy, Oz; 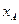, , 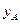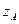- координаты точки приложения силы 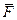; 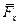, , 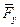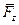- проекции вектора ;

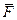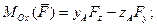
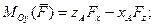
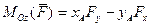- (2)

проекции вектора .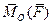

Проекции вектора 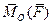на оси Ox, Oy, Oz называются моментом силы 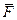относительно этих осей:

. ()

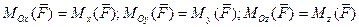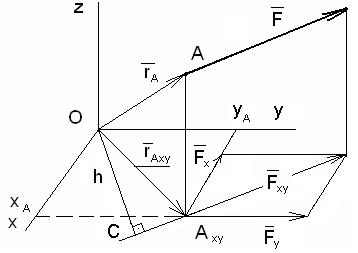
Упражнение 5.1.

Воспользуйтесь Рис.17 и найдите сумму моментов сил и 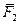относительно осей Ox, Oy, Oz. Убедитесь в том, что момент силы относительно некоторой оси равен нулю, если сила и ось расположены в одной плоскости. В этом случае вектор силы либо пересекает ось, либо ей параллелен.

Момент силы относительно оси можно вычислять по формулам (2), а можно действовать по–другому. Спроецируем вектор 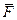на некоторую Рис. 18. Момент силы 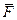относительно оси Oz плоскость Oxy, перпендикулярную оси Oz, Рис.18. В результате получим проекцию 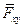, момент которой относительно точки О и есть момент силы 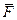относительно оси Oz:

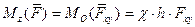; (3)

В нашем случае =+1. Действительно, представив радиус- вектор 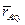и силу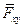

в виде разложений

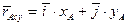; (4)

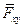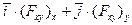= , (5)

можем получить:

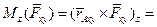
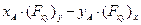
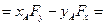
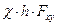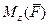= . (6)

Формула (6) совпадает с третьей формулой (2). Поэтому момент силы относительно оси можно вычислять либо по формулам (2), либо по алгоритму, приводящему к равенству (3). Из этого равенства видно, что момент силы относительно оси равен моменту проекции вектора силы на любую плоскость, перпендикулярную этой оси, относительно точки пересечения оси с указанной плоскостью.

Формула (3) показывает, что момент силы относительно оси равен нулю, если линия действия силы пересекает эту ось (в этом случае 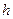=0) или если вектор силы параллелен оси (при этом 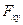=0). Оба этих случая можно объединить в один: “Момент силы относительно оси равен нулю, если вектор силы и ось расположены в одной плоскости”.

5. Пара сил и её свойства.

Рассмотрим две силы 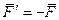, равные по модулю, направленные в противоположные стороны и не лежащие на одной прямой, Рис. 19. Очевидно, что сумма векторов и 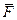, а также сумма их проекций на любую ось, равны нулю. Сумма моментов сил и 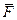относительно точки А равна:

. (1)

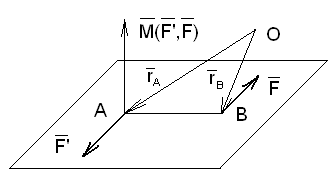
Отсюда следует, что вектор момента пары сил перпендикулярен плоскости, в которой действует пара и направлен так, чтобы при взгляде с его конца поворот тела под действием пары сил был виден происходящим против хода часовой стрелки.

Векторное произведение в правой части (1) количественно определяет действие пары сил на твёрдое тело и называется моментом пары сил.

Убедимся в том, что сумма моментов сил , , 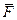( = - 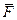) пары относительно любой другой точки будет такой же, как относительно точки А, (1). Для этого найдём сумму моментов этих сил относительно произвольно выбранной точки О, показанной на Рис.19:

=

=

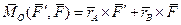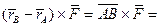
Рис.19. Вектор момента пары сил = 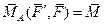. (2)

Из последней формулы следует, что сумма моментов двух сил, образующих пару, относительно любой точки равна моменту (1) этой пары. Значит вектор момента пары сил - свободный аксиальный вектор.

Так как действие пары сил на тело определяется вектором момента этой пары, то допустимы любые преобразования и перемещения пары сил, не изменяющие её момента, а именно:

- можно изменять плечо пары, изменяя при этом и модулисил пары так, чтобы вектор момента пары при этом не изменялся;

- можно перемещать пару сил в плоскости её действия и влюбуюпараллельную плоскость.

Действие на тело совокупности пар сил, расположенных в параллельных и пересекающихся плоскостях, эквивалентно действию на него одной пары сил, момент которой равен геометрической сумме моментов каждой пары сил. Иными словами, пары сил можно складывать. Это утверждение основано на аксиоме аддитивности воздействий, которая будет приведена ниже. Пока же сошлёмся на то, что момент пары сил - свободный вектор, а для таких векторов определено правило сложения. Для пар сил, расположенных в параллельных плоскостях, векторную сумму моментов этих пар при их сложении можно заменить алгебраической суммой, условившись о правиле знаков. Это правило может быть таким же, как и при вычислении моментов сил относительно точки в случае, когда эти силы расположены в одной плоскости (см. формулу (4.3)). Если совокупность пар сил уравновешена, то векторная (или алгебраическая) сумма моментов этих пар равна нулю.

Пару сил можно рассматривать как наглядное представление собственно момента при определении воздействия одного тела на другое.

Дата добавления: 2015-06-04