Уравновешенные системы сил. Условия уравновешенности системы сил. Уравнения равновесия

Назовём уравновешенной такую систему сил, добавление которой к другим

силам, действующим на свободное твёрдое тело, или исключение которой из совокупности действующих на тело сил, не изменяют состояния тела.

Одна сила не может быть уравновешенной. Из опыта известно, что если свободное твёрдое тело покоилось под действием некоторой уравновешенной системы сил, то добавление к ним ещё одной силы, не равной нулю, приведёт тело в движение, т. е. изменит состояние тела. Этот пример показывает, что состояние тела может измениться только в результате воздействий на него других тел.

Две силы могут образовать уравновешенную систему сил лишь в том случае, если они лежат на одной прямой, направлены в противоположные стороны, и их модули равны. Так как воздействия на тело аддитивны по взаимодействующим с ним телам, а векторная сумма двух указанных сил и сумма их моментов относительно любого центра равны нулю, то состояние тела не изменится, если к нему приложить две такие силы (или отбросить их, если они уже действовали на тело). Если к свободному твёрдому телу приложить две равные по модулю и противоположно направленные силы, не лежащие на одной прямой, то состояние тела изменится. Почему?

В соответствии с аксиомой аддитивности воздействий суммарное воздействие других тел на рассматриваемое тело равно векторной сумме воздействий каждого тела. Пусть 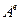- множество 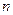тел, с которыми взаимодействует рассматриваемое свободное твёрдое тело 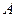. Найдём сумму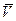 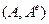всех силовых воздействий

на тело А:

. (1)

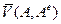- свободный вектор.

Очевидно, что для уравновешенной системы сил должно выполняться условие

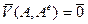. (2)

Однако условия (2) недостаточно для уравновешенности совокупности сил. Если на покоящееся свободное твёрдое тело подействует пара сил, то состояние тела изменится, (тело начнёт вращаться), хотя равенство (2) будет выполнено.

Поэтому надо сформулировать второе условие уравновешенности некоторой системы сил. Воспользуемся аксиомой аддитивности моментных воздействий по телам, оказывающим такие воздействия на выделенное тело, и учтём, что сумма моментов относительно некоторого центра 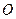двух сил, образующих пару, равна вектору момента этой пары сил. Тогда сумма 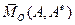моментов относительно опорной точки О всех сил, действующих на это тело со стороны его окружения, определится формулой:

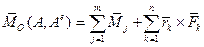, (3)

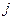Здесь - вектор момента - ой пары сил, действующей на тело; 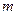- общее число таких пар сил; 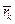- радиус- вектор точки приложения 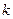- ой силы, исходящий из

центра О.

Чтобы свободное твёрдое тело не вращалось, вектор 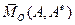должен быть равен нулю:

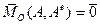. (4)

Величины 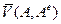и 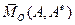называют главным вектором и главным моментом системы сил. Итак, необходимыми и достаточными условиями уравновешенности воздействий других тел на свободное твёрдое тело являются равенства нулю его главного вектора и главного момента относительно любой опорной точки О:

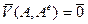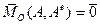; . (5)

Обратим внимание на то, что в условия (5) уравновешенности воздействий входят только внешние силы.

Из условий (5) следуют уравнения равновесия.

Выпишем теперь уравнения равновесия пространственной системы воздействий на свободное твёрдое тело. Проецируя условия (2) и (4) на оси некоторой инерциальной декартовой системы отсчёта 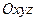, получим шесть уравнений равновесия:

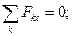
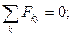
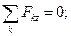(6)

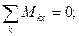
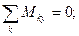
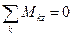. (7)

При получении уравнений (7) учтено определение момента силы относительно оси (см. равенства (5. 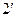)). Каждое уравнение (7) состоит из суммы проекций векторов моментов пар сил и суммы проекций векторов моментов сил, действующих на тело (см. (3)).

Три уравнения (6) указывают на необходимость равенства нулю суммы проекций на каждую из трёх осей некоторой декартовой системы отсчёта 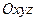всех силовых воздействий на свободное твёрдое тело. Три уравнения (7) моментов относительно каждой из трёх осей той же системы отсчёта показывают, что сумма моментов этих сил (включая пары сил) относительно каждой из этих осей также должна быть равна нулю, если эта система сил уравновешена.

Если воздействия на свободное твёрдое тело расположены в одной плоскости, то из шести уравнений (6), (7) будут иметь смысл только три уравнения: два уравнения проекций сил на оси и одно уравнение моментов сил относительно точки:

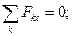
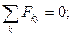
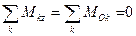. (8)

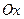Оси и 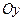, на которые проецируются силы, и точка, относительно которой пишется уравнение моментов, в системе уравнений (8), расположены в плоскости воздействий на тело.

Для систем, находящихся в равновесии, расстояния между двумя любыми их точками изменяться не может, что характерно для абсолютно твёрдого тела. Это означает, что уравнения равновесия применимы не только к одному телу, но и к изменяемой системе связанных между собой твёрдых тел, а также к деформируемым телам, например, к гибким нитям. Иными словами, при рассмотрении равновесия изменяемых и деформируемых систем, они считаются как бы затвердевшими. Это утверждение называют принципом отвердевания.

Дата добавления: 2015-06-04