Равновесие рычага, нагруженного противоположно направленными параллельными силами

На Рис.25 показан находящийся в равновесии невесомый рычаг АВ, нагруженный по концам противоположно направленными неравными параллельными силами и 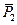. Пусть для определённости 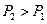. Рычаг на Рис.25 можно рассматривать как схему тачки, колесо которой в точке О опирается на землю; 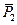- вес тачки с грузом, а - суммарная сила, которую рабочий прикладывает к её ручкам. С помощью тачки человек может приподнять такой груз, который он непосредственно руками поднять не в состоянии.

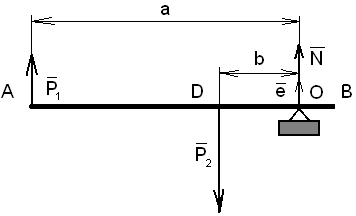Первое условие уравновешенности сил, действующих на рычаг, Рис.25, имеет вид 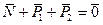. (1)

Из этого условия находим реакцию опоры в точке О: 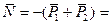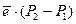; (2)

.

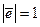Приравняем нулю сумму моментов относительно опорной точки О сил, действующих на рычаг:

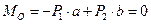. (3) Рис.25. Рычаг, нагруженный

Из (3) следует равенство противоположно направленными силами

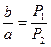, (4)

показывающее, что опорная точка О расположена вне отрезка AD ближе к точке

приложения большей силы.

Из (2) и (4) видно, что при стремлении модуля силы 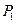к модулю силы , реакция 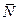устремляется к нулю, а опорная точка О уходит в бесконечность. Действительно, 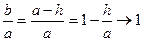, и, значит, 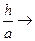0, ; .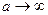

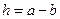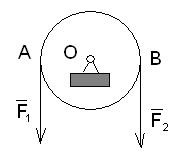Выполненный анализ показывает, что совокупность двух равных по модулю, противоположно направленных сил, не лежащих на одной прямой, не может быть эквивалентна одной силе. Как уже указывалось, такая система двух сил образует пару сил, действие которой на тело характеризуется вектором её момента (см. Раздел 5).

Упражнение.

На Рис.26 изображён простой блок, через который переброшена верёвка. Такой блок можно рассматривать как равноплечий рычаг. Пусть к одному концу верёвки прикреплена люлька, в которой сидит человек. С какой силой он должен тянуть другой конец верёвки, чтобы поднимать самого себя? Рис.26. Простой блок.

13. Действия над распределёнными нагрузками.

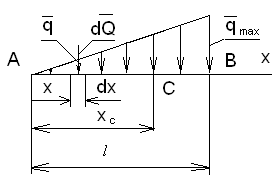
Пусть на прямолинейный участок АВ некоторого тела G со стороны другого тела H действует нагрузка, распределённая по линейному закону, Рис.27. Как оценить воздействие тела H на тело G?

Определим сначала силовую часть искомого воздействия.

Построим ось Ax и выделим на расстоянии x от начала А элементарный участок

длины dx. Интенсивность 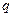нагрузки в точке 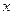найдём из подобия прямоугольных треугольников с катетами 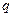и :

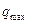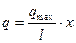. (1)

Сила 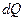, приходящаяся на участок ,

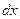определяется формулой

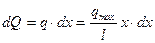. (2)

Если представить весь отрезок АВ разделённым на элементарные участки, то совокупное силовое воздействие на тело G равно сумме сил, действующих на каждый

Рис.27. Нагрузка, распределённая по участок, то есть равно интегралу

линейному закону . (3)

Теперь найдём моментную часть воздействия тела H на тело G, приняв в качестве опорной точки некоторую точку О, Рис. 28. Момент относительно точки О элементарной силы равен

. (4)

В соответствии с Рис.28 представим радиус- вектор 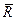в виде суммы 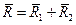, и учтём в (4) формулу (2). Примем во внимание, что 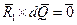. В результате формула (4) может быть преобразована к виду

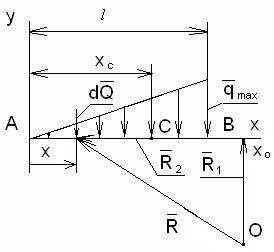
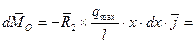
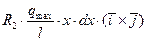= . (5)

Здесь ;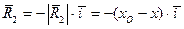

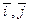- орты осей Ox и Oy; , -

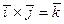орт оси Oz, направленной перпендикулярно чертежу на нас.

Представим выражение (5) в скалярной форме, учитывая, что, момент относительно точки О силы положителен в соответствии с принятым правилом знаков:

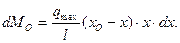(6) Рис.28. К вычислению момента

Интегрируя (6) по переменной x в пределах распределённой нагрузки от нуля до 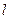, получим окончательное значение момента рассматриваемой нагрузки относительно точки О

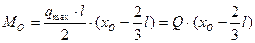. (7)

Как видно из последней формулы, искомый момент получился равным моменту силы 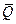, приложенной в точке С с абсциссой

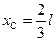. (8)

Нетрудно понять, что точка С - это центр силового воздействия тела H на тело G. Иными словами, если в качестве точки приведения выбрать точку С, то тело H не будет сопротивляться поворотам тела G вокруг точки С. Учитывая сказанное, часто на исходных силовых схемах нагрузку на тело, распределённую по линейному закону, сразу заменяют силой, определяемой формулой (3), и приложенной в центре С силового воздействия, координата которого задана формулой (8). Напомним, что в данном пособии сила - свободный вектор, и говорить о точке её приложения целесообразно только для исходной, заданной схемы нагружения конструкции.

Если нагрузка на некоторый участок тела длины 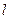распределена равномерно с интенсивностью 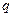, то суммарное силовое воздействие на тело получается равным

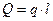, а центр силового воздействия расположен посередине отрезка .

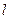Дата добавления: 2015-06-04