
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пара сил
|
|
|
|
Аналитическое задание и сложение сил
Силы можно задавать и складывать аналитически с помощью их проекций на оси координат (рис. 1.8, 1.9).
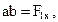
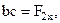
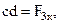
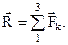
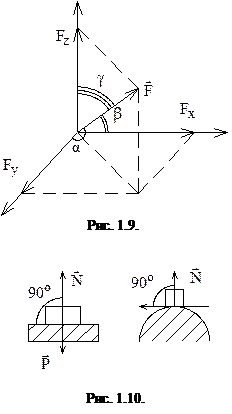
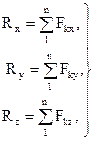 (1.3)
(1.3) 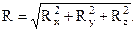 (1.4)
(1.4)

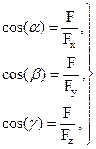 (1.5)
(1.5) 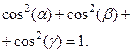
Очевидно, аналитически можно сложить любое число сил. Следует однако заметить, что при этом мы получим не равнодействующую, а главный вектор системы (в отдельных случаях он может являться равнодействующей).
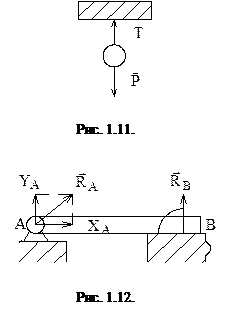 1.4. Связи и реакции
1.4. Связи и реакции
связей
Связями будем называть все те тела, которые ограничивают перемещение данного тела.
Условились действия связей на тело заменять силами, которые называются реакциями связей.
Очевидно, реакции связей всегда направлены в сторону, противоположную тому перемещению, которое они ограничивают.
Типы связей
Характер связей, т.е. соединения тел, исключительно многообразен. Для выявления основных особенностей взаимодействия контактирующих между собой тел связи обычно упрощают, относя их к тому или иному типу. Рассмотрим наиболее часто встречающиеся типы связей.
1. Гладкая поверхность (пренебрегаем трением). Реакция гладкой поверхности перпендикулярна этой поверхности (рис. 1.10).
2. Гибкая нить. Реакция нити всегда направлена по нити (рис. 1.11).
3. Неподвижный цилиндрический шарнир (подшипник).
В данном случае направление реакции и ее величина неизвестны и для их определения реакцию раскладывают по осям Х и У (рис. 1.12).
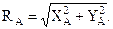
4. Подвижный цилиндрический шарнир.
 Реакция подвижного цилиндрического шарнира направлена перпендикулярно плоскости возможного перемещения (рис. 1.13).
Реакция подвижного цилиндрического шарнира направлена перпендикулярно плоскости возможного перемещения (рис. 1.13).
5. Жесткая заделка.
Реакция в данном случае состоит из трех компонентов: сил по осям Х, У и реактивного момента неизвестного направления (рис. 1.14).
Глава2. Системы сходящихся и параллельных сил
2.1. Сложение и
равновесие системы сходящихся сил
Если силы таковы, что линии действия их пересекаются в одной точке, то такая система сил называется сходящейся.
Очевидно, пользуясь аксиомой 3 такую систему сил можно заменить одной, их равнодействующей:
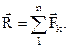
Величина и направление равнодействующей определяются замыкающей стороной силового (векторного) многоугольника (рис. 1.15). Для построения такого многоугольника каждая последующая сила откладывается из конца предыдущей силы. Линия действия равнодействующей проходит через точку пересечения сил.
Таким образом, для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник был бы замкнутым (рис. 1.16).
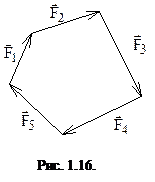 Следовательно в аналитическом виде можно записать для системы сходящихся сил:
Следовательно в аналитическом виде можно записать для системы сходящихся сил:
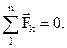
Значит:
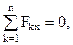 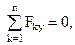 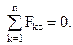
| (1.6) |
Уравнения (1.6) определяют аналитические условия равновесия системы сходящихся сил.
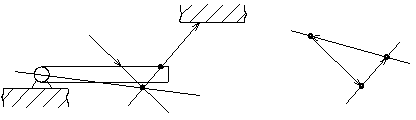
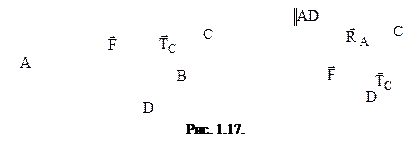 Теорема: е сли тело находится в равновесии под действием трех непараллельных сил, то эти силы пересекаются в одной точке.
Теорема: е сли тело находится в равновесии под действием трех непараллельных сил, то эти силы пересекаются в одной точке.
Из предыдущего следует, что эти три силы составляют замкнутый треугольник. Складывая любые две из них по аксиоме 3 замечаем, что тело будет находится в равновесии под действием двух сил. Но из аксиомы 1 вытекает, что эти две силы направлены по одной прямой, т.е. линии действия всех сил пересекаются в одной точке.
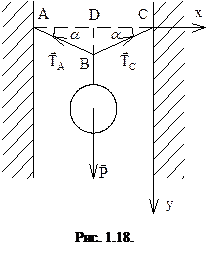 На основе этой теоремы можно непосредственно определять направление неизвестных реакций связей. Так, например, для невесомой балки AB (рис. 1.7) реакция неподвижного цилиндрического шарнира A пройдет через точку пересечения силы
На основе этой теоремы можно непосредственно определять направление неизвестных реакций связей. Так, например, для невесомой балки AB (рис. 1.7) реакция неподвижного цилиндрического шарнира A пройдет через точку пересечения силы 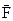 и натяжения нити
и натяжения нити 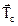 . При известной силе
. При известной силе 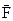 величина реакции
величина реакции 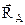 найдется построением силового треугольника.
найдется построением силового треугольника.
Пример 1.1. Определить натяжения троса ABC, на котором подвешен уличный фонарь весом 150 Н. (рис. 1.18). Длина всего троса равна 20 м, отклонение от горизонта BD=0,1 м. Весом троса пренебречь.
Решение. На основе условий равновесия системы схождения сил (1.6) можно записать:
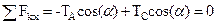 , ,
| (а) |
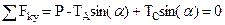
| (б) |
Из уравнения (а) находим  . Тогда из (б) найдем
. Тогда из (б) найдем 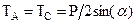 . По условию задачи
. По условию задачи  , откуда
, откуда 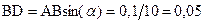 . Следовательно
. Следовательно 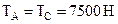 , т.е. натяжение троса в 50 раз превышает вес фонаря. Увеличение веса фонаря, например за счет намерзания на нем льда, может привести к обрыву троса.
, т.е. натяжение троса в 50 раз превышает вес фонаря. Увеличение веса фонаря, например за счет намерзания на нем льда, может привести к обрыву троса.
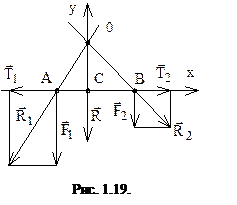 2.2. Сложение системы параллельных сил
2.2. Сложение системы параллельных сил
Теорема 1. Равнодействующая двух параллельных сил направленных в одну сторону им параллельна, при этом модуль равнодействующей равен сумме модулей слагаемых сил, а линия действия ее делит расстояние между силами на части, обратно пропорциональные силам.
Две параллельные силы 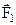 и
и 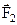 можно преобразовать в две сходящиеся силы
можно преобразовать в две сходящиеся силы  и
и 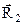 (рис. 1.19), которая на основе аксиомы 3 может быть заменена из равнодействующей
(рис. 1.19), которая на основе аксиомы 3 может быть заменена из равнодействующей 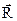 . Для этого приложим в точках A и B две уравновешенные силы
. Для этого приложим в точках A и B две уравновешенные силы 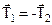 . Тогда с учетом аксиомы 2 получим:
. Тогда с учетом аксиомы 2 получим:
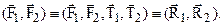
Найдем модуль равнодействующей:
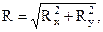
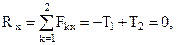
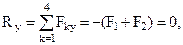 т.е.
т.е.
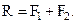
| (1.7) |
Рассматривая подобие треугольников АСО и треугольника ВСО с соответствующими силовыми треугольниками можно найти следующее отношение:

| (1.8) |
Очевидно, полученные выводы позволяют сложить любое число параллельных сил, направленных в одну сторону. Таким образом, система указанных параллельных сил всегда может быть заменена одной силой – их равнодействующей.
Теорема 2. Равнодействующая двух параллельных сил, направленных в противоположные стороны, им параллельна, направлена в сторону большей силы и делит расстояние между силами внешним образом на части обратно, пропорциональные силам.
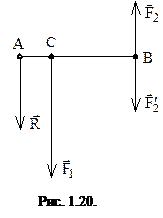 Пусть для определенности
Пусть для определенности 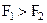 (рис. 1.20). Пользуясь предыдущим результатом разложим силу
(рис. 1.20). Пользуясь предыдущим результатом разложим силу 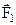 на две ей параллельные силы:
на две ей параллельные силы: 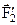 , приложенную в точке B и равную по модулю силе
, приложенную в точке B и равную по модулю силе 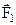 , и силу
, и силу 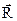 , величина и точка приложения которой найдется из выражения:
, величина и точка приложения которой найдется из выражения:
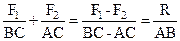 . .
| (1.9) |
Так как силы 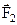 и
и 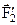 уравновешены, то на основе аксиомы 2 их можно отбросить. Следовательно, оставшаяся сила
уравновешены, то на основе аксиомы 2 их можно отбросить. Следовательно, оставшаяся сила 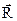 будет являться равнодействующей антипаралллельных сил
будет являться равнодействующей антипаралллельных сил 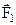 и
и 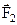 .
.
Теорема 3. Если тело находится в равновесии под действием трех сил, две из которых параллельны и не равны, то третья сила им параллельна.
В самом деле, складывая эти две силы устанавливаем, что, во-первых, их равнодействующая им параллельна и во-вторых, что тело находится в равновесии под действием двух сил, которые по аксиоме 1 должны быть параллельны по одной прямой. Следовательно, третья сила параллельна заданным.
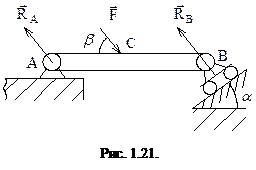 Так, например, для невесомой балки BA (рис. 1.21) при
Так, например, для невесомой балки BA (рис. 1.21) при 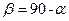 реакция неподвижного цилиндрического шарнира
реакция неподвижного цилиндрического шарнира 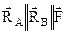 . Если AC=CB, то как это следует из (1.9),
. Если AC=CB, то как это следует из (1.9), 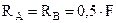 .
.
Из (1.9) следует, что две антипараллельные равные силы не имеют равнодействующей, т.е. их нельзя заменить одной силой. Такая система двух равных антипараллельных сил называется парой сил. Очевидно, пара сил оказывает вращательный эффект на тело. Этот вращательный эффект однозначно определяется тремя параметрами:
- плоскостью действия;
- направлением поворота;
- 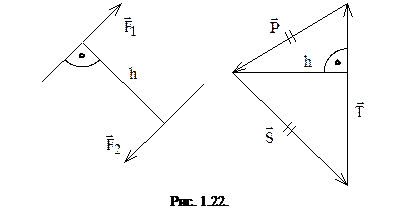 модулем (величиной) момента пары, который равен произведению модуля одной из сил пары на расстояние между силами.
модулем (величиной) момента пары, который равен произведению модуля одной из сил пары на расстояние между силами.
На рис. 1.22 изображен две пары сил, моменты которых определяются выражениями:
 , , 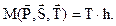
| (1.10) |
Момент пары сил считается положительным, если поворот наблюдается происходящим против часовой стрелки отрицательным, если пара сил поворачивается по часовой стрелке.
Свойства пары сил
1. Действие пары сил на тело не изменится, если у нее произвольным образом изменить силы и плечо таким образом, чтобы их произведение оставалось постоянным, т.е. при неизменном моменте пары.
2. Пару сил можно переносить в плоскости ее действия, при этом сохраняются все параметры пары сил.
3. Пару сил можно повернуть в плоскости ее действия на любой угол.
4. Действие нескольких пар сил, приложенных в одной плоскости можно заменить одной парой сил, момент которой равен алгебраической сумме заданных пар сил.
Условие эквивалентности двух пар сил
Две пары сил будут эквивалентными (взаимозаменяемыми), если они имеют общую плоскость действия, одинаковые направления и равные моменты.
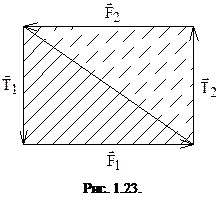 На рис. 1.23 изображены две эквивалентные пары сил
На рис. 1.23 изображены две эквивалентные пары сил
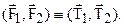
|
|
|
|
|
Дата добавления: 2015-06-04; Просмотров: 569; Нарушение авторских прав?; Мы поможем в написании вашей работы!