Приведение плоской системы сил к данному центру

Докажем необходимость и достаточность условий равновесия (1.11)-(1.13). Для этого возьмем любую произвольную плоскую систему сил, и, пользуясь теоремой о параллельном переносе силы, перенесем все заданные силы в точку О.

Дано: 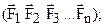требуется упростить данную систему сил (рис. 1.29,а). Перенесем все силы параллельно самим себе в произвольную точку 0, добавив при этом присоединенные пары сил, моменты которых равны моментам заданных сил относительно центра приведения 0.

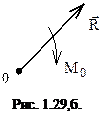Таким образом после переноса всех сил в точку 0 мы получили систему 2 n параметров. Так как все силы пересекаются в одной точке О, то их всегда можно сложить по аксиоме 3 и заменить одной силой, которая называется главным вектором системы:

(1.14)

Так как присоединенные пары сил расположены в одной плоскости, то их можно сложить и заменить одной парой сил, момент которой называется главным моментом системы M₀:

(1.15)

Вывод. Любую плоскую систему сил всегда можно заменить одной силой – главным вектором 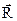– и одной парой сил – главным моментом М₀ (рис. 1.29,б).

Случаи приведения плоской системы сил

1. R 0; М₀=0 – случай равнодействующей.

В этом единственном случае главный вектор системы является ее равнодействующей.

2. R=0; М₀ 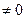– случай результирующей пары сил. В этом единственном случае величина и направление главного момента не зависят от выбора центра приведения.

3. R 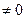;M₀ 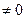– общий случай. Можно показать, что общий случай всегда можно привести к одной равнодействующей в новом центре приведения .

4. R=0; M₀=0 – случай равновесия плоской системы сил.

Очевидно, для того, чтобы имел место случай 4, необходимо и достаточно, чтобы для заданной системы сил выполнялись условия (1.11)-(1.13).

Дата добавления: 2015-06-04