Равновесие системы тел

Приведение произвольной плоской системы сил к равнодействующей

Найдем такую точку , в которой заданная система сил приводится к равнодействующей (рис. 1.30).

Воспользуемся теоремой о параллельном переносе силы.

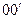Перенесем главный вектор в точку , при этом расстояние выберем из условия:

.

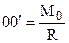(1.16)

Силу R в точке 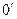обозначим и добавим присоединенный момент

.

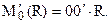(1.17)

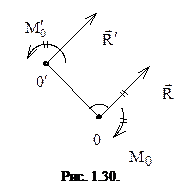Из сравнения (1.16) и (1.17) следует, что главный момент 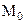и присоединенный момент равны по величине и противоположны по направлению, т.е. в сумме они дают 0. Следовательно 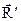является равнодействующей данной системы сил.

Очевидно, изложенный метод может быть применен всегда, т.е. произвольную плоскую систему сил можно привести либо к равнодействующей (случай 1), либо к паре сил (случай 2).

В реальных условиях в равновесии как правило находится система тел, связанных между собою известным образом. Т.к. вся система тел находится в равновесии, то, очевидно, каждое из тел, входящих в систему, также находится в равновесии и для каждого из этих тел можно записать условия равновесия (1.11)-(1.13). Это позволит определить внутренние реакции связей. Следовательно, в общем случае число уравнений равновесия будет равно S=k*n, где k- число условий равновесия для одного тела. n – число тел.

Пример 1.4. Определить реакции шарниров A, B, C, для конструкции, изображенной на рис. 1.31.

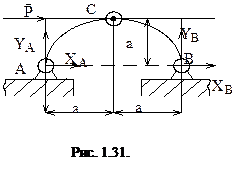Рассмотрим равновесие системы двух тел для которых:

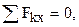
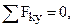
Составим уравнения равновесия:

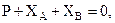
	(а)
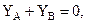
	(б)
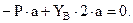
	(в)

Так как в этих уравнениях содержится 4 неизвестных, то для увеличения числа уравнений рассмотрим отдельно равновесие тела АС (рис. 1.32):

	(г)
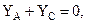
	(д)
	(е)

Из уравнений (а)-(е) найдем:

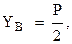
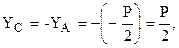
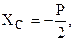
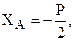
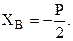
Так как некоторые проекции реакций получились с минусом, то в действительности они направлены в сторону противоположную указанной на рис. 1.31 и 1.32.

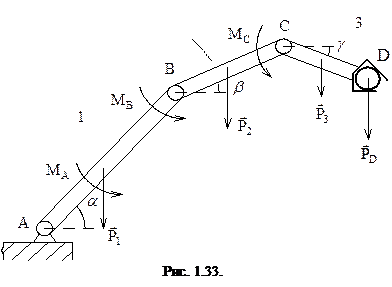Пример 1.5. Механизм робота-манипулятора состоит их трех звеньев, которые в положении равновесия расположены в вертикальной плоскости (рис. 1.33). Определить моменты сил приводов в шарнирах A, B, С, если длины звеньев l ₁ = 0,8 м, l ₂ = 0,5 м, l ₃ = 0,3 м, их массы , , 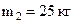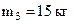. Рука манипулятора CD несет груз массой 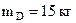. Звенья считать однородными стержнями; , .

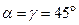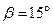Решение. Для определения момента в шарнире C рассмотрим отдельно равновесие рука CD. Очевидно, для определения 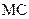достаточно найти сумму моментов действующих на звено 3 сил и прировнять ее нулю. Заметим, что реакции шарнира C x_C и y_С момента относительно точки C не не создают ()на рисунке они не показаны. Тогда

.

Аналогично для звеньев 2 и 3 имеем:

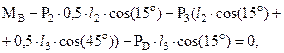
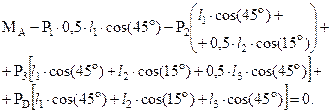
Решая полученные уравнения относительно искомых моментов, получим:

; ; .

Дата добавления: 2015-06-04