Опоры и опорные реакции балок

Условия равновесия произвольной плоской системы сил

Теорема Вариньона о моменте равнодействующей

Если система сил имеет равнодействующую 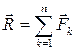, то момент равнодействующей относительно любого центра О равен сумме моментов всех сил системы относительно того же центра О:

.

Пример 3. Найти момент силы 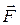относительно точки О (рис. 6).

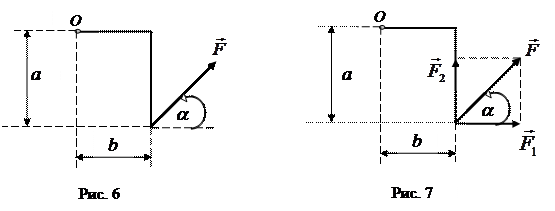Решение. Разложим силу на составляющие и (рис. 7), причем .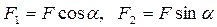

Момент силы 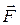относительно точки О найдем по теореме Вариньона:

.

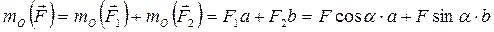Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на каждую координатную ось (x, y) и алгебраическая сумма моментов этих сил относительно любой точки, лежащей в плоскости действия сил, были равны нулю.

1. Шарнирно–подвижная опора (рис. 8) допускает поворот вокруг оси шарнира и линейное перемещение параллельно опорной плоскости. Если пренебречь трением на опоре и в шарнире, то реакция такой связи будет направлена перпендикулярно опорной плоскости и неизвестна только по модулю (одно неизвестное).

2. Шарнирно–неподвижная опора (рис. 9) допускает только поворот вокруг оси шарнира и не допускает никаких линейных перемещений. Реакция такой опоры будет направлена перпендикулярно оси шарнира, модуль и направление ее заранее не известны. Обычно при решении задач такую реакцию разлагают на две взаимно перпендикулярные составляющие, не известные по модулю, но известные по направлению.

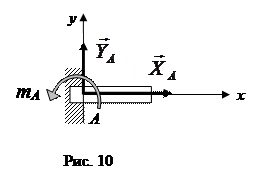
3. Жесткая заделка (рис. 10) не допускает ни линейных перемещений, ни поворотов защемленного конца балки. Поэтому реакцию жесткой заделки заменяют силой реакции 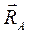, не известной по модулю и направлению, и парой сил m_A, момент которой также не известен. Силу реакции 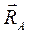разлагают на две взаимно перпендикулярные составляющие и .

Таким образом, для нахождения реакции жесткой заделки надо определить три неизвестные величины , и m_A.

Дата добавления: 2015-06-04