Решение. 1. Установим, является ли ферма жесткой

1. Установим, является ли ферма жесткой.

Данная ферма состоит из m = 13 стержней и n = 8 узлов и для нее выполняется соотношение m = 2 n - 3 (13 = 16 – 3), поэтому данная ферма является жесткой без лишних стержней.

2. Определение реакций опор.

Для определения опорных реакций рассмотрим равновесие фермы в целом как единого твердого тела. На нее действуют заданные силы 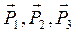и реакции связей 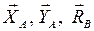(рис. С2, а).

Составим условия равновесия для полученной плоской системы сил:

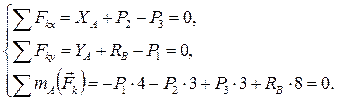
Решая полученную систему, найдем

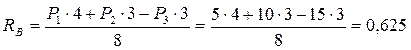кН.

Y_A = P ₁– R_B = 5– 0,625 = 4,375 кН, X_A = Р ₃ - P ₂ = 15 – 10 = 5 кН.

3. Определение усилий в стержнях фермы методом вырезания узлов.

Стержни, сходящиеся в узле фермы, являются для данного узлового соединения связями. Отбросим мысленно связи и заменим их действие на узлы реакциями. Направления реакций всех стержней покажем от узлов внутрь стержня в предположении, что стержни растянуты. Если в результате решения реакция стержня получится отрицательной, это будет означать, что соответствующий стержень сжат.

Рассмотрим узел А, к которому приложены только два неизвестных усилия 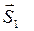и 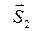(рис. С2, б).

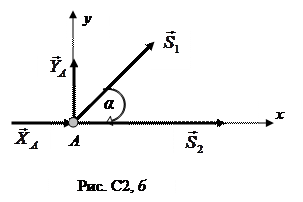
Составим для этого узла условия равновесия:

Из треугольника ACD (рис. С2, а) найдем

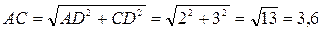м,

.

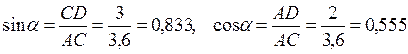Из уравнений равновесия находим:

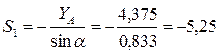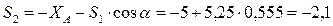кН.

кН

Зная 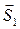и , перейдем к узлу С (рис. С2, в).

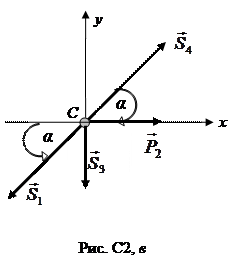Условия равновесия имеют вид:

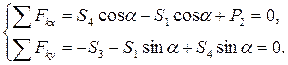
Решая полученные уравнения, найдем

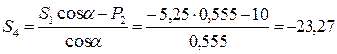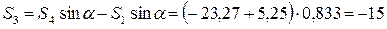кН,

кН.

Рассмотрим узел D (рис. С2, г)

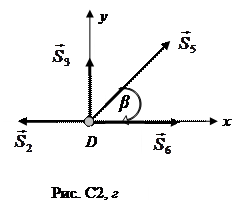Для узла D условия равновесия имеют вид:

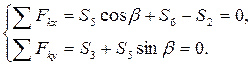
Из треугольника DEK (рис. С2, а) найдем

м,

.

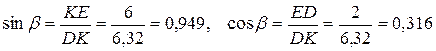Из уравнений равновесия находим

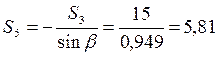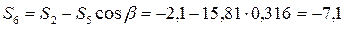кН,

кН.

Таким образом, усилия в стержнях 4, 5 и 6 равны:

S ₄ = -23,27 кН, S ₅ = 15,81 кН, S ₆ = -7,1 кН.

Знаки усилий показывают, что стержень 5 растянут, а стержни и 4 и 6 сжаты.

4. Определение усилий в стержнях методом сечений.

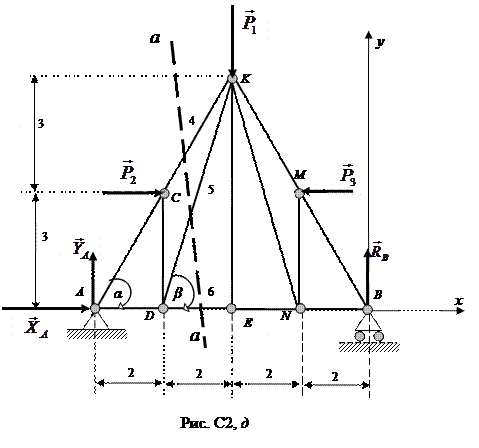
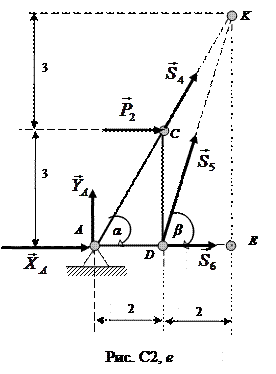
Для определения усилий S ₄, S ₅ и S ₆ мысленно разрежем ферму сечением а – а (рис. С2, д) и рассмотрим левую часть фермы (рис. С2, е). Действие отброшенной правой части на левую представим силами .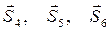

По-прежнему условно предполагаем, что стержни растянуты. Знак «минус» в ответе укажет на то, что стержень сжат.

Усилие S ₅ найдем из уравнения

.

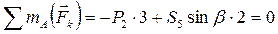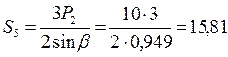кН.

Для определения S ₆ составим уравнение

.

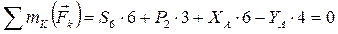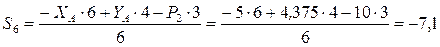кН.

Усилие S ₄ найдем из уравнения

.

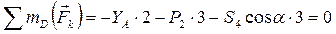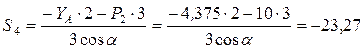кН.

Ответ: S ₄ = -23,27 кН, S ₅ = 15,81 кН, S ₆ = -7,1 кН.

РАВНОВЕСИЕ СИСТЕМЫ ТВЕРДЫХ ТЕЛ

В статике твердого тела наряду с равновесием одного тела рассматриваются системы сочлененных материальных тел, т.е. совокупности твердых тел, касающихся друг друга своими поверхностями или соединенных друг с другом шарнирами, гибкими нитями или стержнями.

При решении задач, в которых рассматривается равновесие системы тел, число неизвестных может превысить число уравнений статики, составленных для системы в целом. Кроме того, часто требуется найти силу, с которой одно сочлененное тело действует на другое. Для решения таких задач необходимо рассматривать равновесие каждого тела отдельно, составляя для него соответствующие уравнения равновесия. При этом остальные тела составной системы являются связями, наложенными на рассматриваемое тело. Метод, основанный на рассмотрении равновесия отдельных частей системы твердых тел, называют методом расчленения.

Задачи на равновесие системы сочлененных тел, находящихся под действием произвольной плоской системы сил, рекомендуется решать в следующем порядке:

1. Выделить систему сочлененных тел, равновесие которых нужно рассмотреть.

2. Изобразить активные (заданные) силы.

3. Отбросить связи, заменив их реакциями связей.

4. Убедиться в том, что систему в целом, как одно твердое тело, решить нельзя (число неизвестных более трех).

5. Наметить общий путь решения, т.е. принять, как целесообразнее расчленить данную систему: рассматривать равновесие каждого из сочлененных тел отдельно или же всей системы в целом и некоторых тел. Определить общее количество искомых сил.

Затем необходимо определить общее количество независимых уравнений равновесия, которые можно составить при данном расчленении. В статически определимой задаче число неизвестных должно равняться числу уравнений равновесия.

6. Выбрать систему координат.

7. Составить уравнения равновесия для каждого твердого тела или для каждой системы тел, равновесие которых исследуется.

8. Решить систему всех уравнений равновесия.

Задача С3

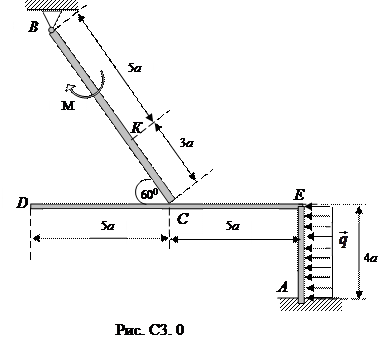
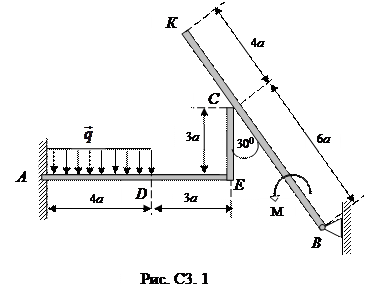
Балка ВС и уголок соединены шарниром в точке С или свободно опираются друг на друга (рис. С3.0 – С3.2). На конструкцию действуют пара сил с моментом М = 20 Нм, равномерно распределенная нагрузка интенсивности q = 5 Н/м и две силы. Эти силы, их направления и точки приложения указаны в табл. С3.

Определить реакции связей в точках А, В и С, вызванные действующими нагрузками. При окончательных расчетах принять а = 0,5 м.

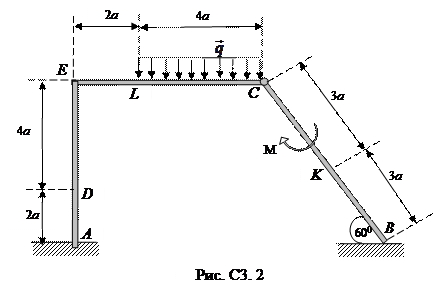Таблица С3

Силы

F ₁ = 10 Н

F ₂ = 20 Н

F ₃ = 30 Н

F ₄ = 40 Н

Номер условия

Точка приложения  

α ₁, град.

Точка приложения

α ₂, град.

Точка приложения

α ₃, град.

Точка приложения

α ₄, град.

K

-

-

E

-

-

-

-

D

-

-

K

-

-

K

D

-

-

D

-

-

K

-

-

K

-

-

-

-

D

E

K

-

-

-

-

-

-

-

-

K

E

-

-

E

-

-

K

K

D

-

-

-

-

-

-

-

-

K

E

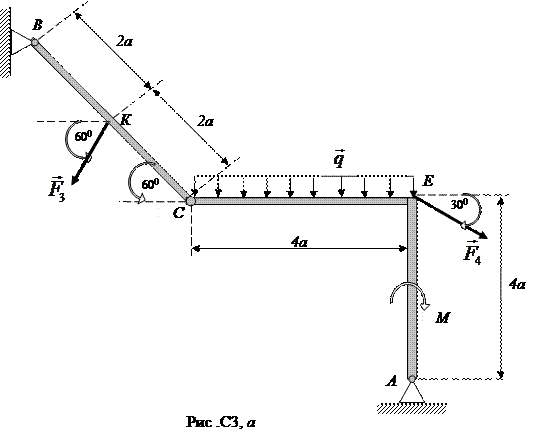
Пример С3. Балка ВС и уголок соединены шарниром в точке С. На конструкцию действуют пара сил с моментом М, равномерно распределенная нагрузка интенсивности 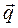и две силы 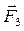и 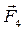(рис. С3, а).

Определить реакции связей в точках А, В и С, вызванные действующими нагрузками, если М = 20 Нм, q = 5 Н/м, F ₃ = 30 H, F ₄ = 40 H, а = 0,5 м.

Решение.

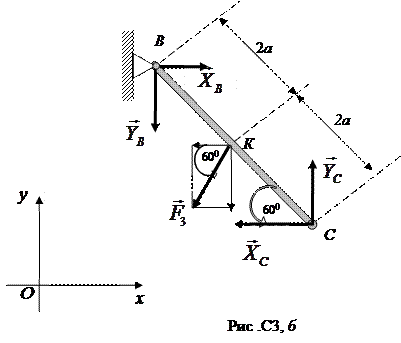
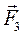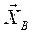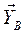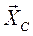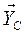1. Для определения реакций связей расчленим систему и рассмотрим равновесие балки ВС (рис. С3, б). Изображаем действующие на балку силы: активную силу , составляющие и шарнира В, и , составляющие шарнира С. Для полученной плоской системы сил составим три уравнения равновесия:

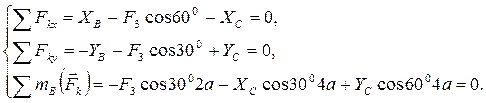
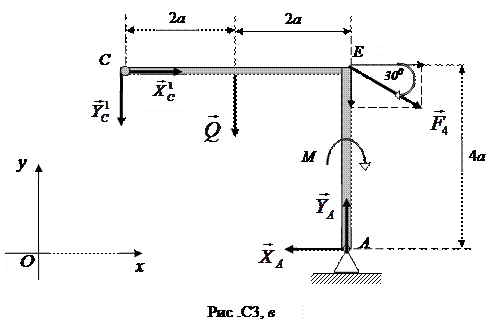
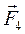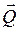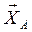2. Теперь рассмотрим равновесие уголка (рис. С3, в). На тело действуют пара сил с моментом М, активная сила , равномерно распределенная нагрузка, которую заменим силой , приложенной в середине участка СЕ (численно ). Реакцию шарнира А разложим на составляющие и 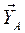. Реакцию шарнира С представим в виде двух составляющих 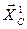и 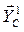, которые, согласно аксиоме статики о равенстве действия и противодействия, равны по модулю и противоположны по направлению силам 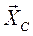и 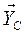, т.е. , .

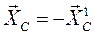Для этой плоской системы сил составим три уравнения равновесия:

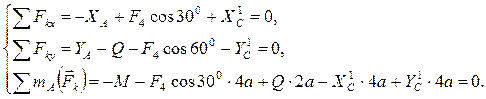
3. Решаем полученные системы уравнений. Подставим данные задачи в уравнения:

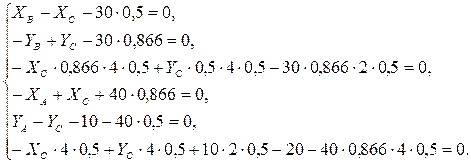
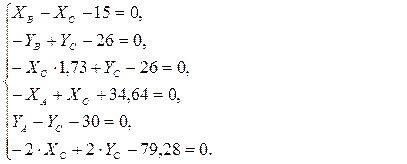
Из третьего уравнения находим 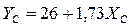и подставляем в шестое уравнение:

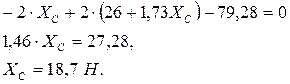
Тогда .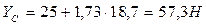

Их первого уравнения найдем: .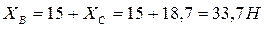

Из второго уравнения .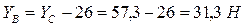

Из четвертого уравнения .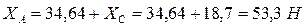

Из пятого уравнения .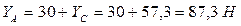

Ответ: Х_А = 53,34 Н, Y_А = 87,3 Н, Х_В = 33,7 Н, Y_В = 31,3 Н,

Х_С = 18,7 Н, Y_С = 57,3 Н.

Дата добавления: 2015-06-04