Расчет плоских ферм

При перекрытии больших пролетов (мосты, промышленные здания и т.п.) и в крупных строительных кранах часто применяются сквозные конструкции, называемые фермами.

Фермой называется жесткая конструкция из прямолинейных стержней, соединенных на концах шарнирами. Если все стержни фермы лежат в одной плоскости, ферму называют плоской. Места соединения стержней фермы называют узлами.

Все внешние нагрузки к ферме прикладываются только в узлах. При расчете фермы трением в узлах и весом стержней пренебрегают. Стержни фермы работают только на растяжение или на сжатие. Ограничимся рассмотрением жестких плоских ферм, без лишних стержней, образованных из треугольников. В таких фермах число стержней m и число узлов n связаны соотношением

m = 2 n -3.

Если m> 2 n- 3, то ферма статически неопределимая;

если m< 2 m- 3, конструкция перестает быть геометрически неизменяемой, получает подвижность (становится механизмом).

Расчет ферм сводится к определению опорных реакция и усилий в ее стержнях.

Опорные реакции находят обычными методами статики, рассматривая ферму в целом как твердое тело.

Усилия в стержнях можно определить двумя методами.

Метод вырезания узлов. Этим методом удобно пользоваться, когда надо найти усилия во всех стержнях фермы. Он сводится к последовательному рассмотрению условий равновесия сил, сходящихся в каждом узле.

При решении задач методом вырезания узлов рекомендуется такая последовательность действий:

1. Определить реакции опор, пользуясь уравнениями равновесия для всей фермы, рассматривая её как твердое тело;

2. Вырезать узел, в котором сходятся два стержня, и, рассматривая его равновесие под действием активных сил и реакций разрезанных стержней; определить эти реакции из двух уравнений проекций сил, приложенных к узлу, на декартовы оси координат;

3. Переходя от узла к узлу, рассматривать аналогично равновесие каждого узла; при этом в каждом узле должно быть только два неизвестных усилия в стержнях.

Метод сечений (метод Риттера). Этим методом удобно воспользоваться для определения усилий в отдельных стержнях фермы, в частности, для проверочных расчетов. Идея метода состоит в том, что ферму разделяют на две части сечением, проходящим через три стержня, в которых (или в одном из которых) требуется определить усилия, и рассматривают равновесие одной из этих частей. Действие отброшенной части заменяют соответствующими силами, направляя их вдоль разрезанных стержней от узлов, т.е. считая стержни растянутыми. Затем составляют уравнения равновесия, беря центры моментов (или ось проекций) так, чтобы в каждое уравнение вошло только одно неизвестное усилие.

При расчете ферм методом сечений рекомендуется такая последовательность действий:

1. Определить реакции опор, пользуясь уравнениями равновесия для всей фермы, рассматривая её как твердое тело;

2. Разрезать мысленно ферму, к которой приложены все внешние силы, на две части так, чтобы число разрезанных стержней не превышало трех, и заменить действие отброшенной части искомыми усилиями стержней, полагая, все стержни растянутыми;

3. Составить уравнения равновесия для части фермы так, чтобы в каждое уравнение входило одно неизвестное усилие. Для этого нужно составить уравнение моментов относительно точек, где пересекаются линии действия двух неизвестных усилий; или, если два стержня параллельны, то можно составить уравнение проекций на ось, перпендикулярную этим стержням, в которое также войдет одно неизвестное усилие;

4. Решая каждое из составленных уравнений, найти искомые усилия в стержнях; если в ответе получается знак «минус», то это означает, что стержень сжат, а не растянут.

ЗАДАЧА С2

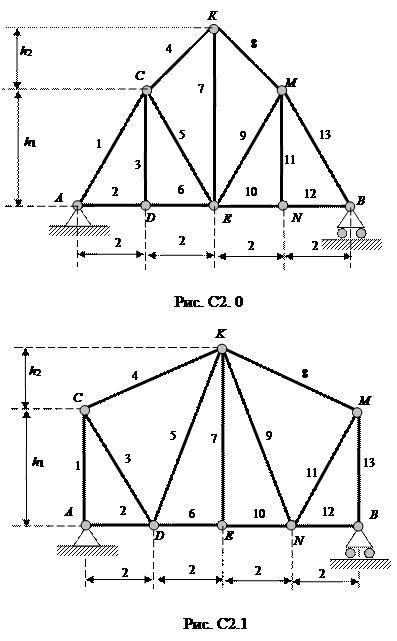
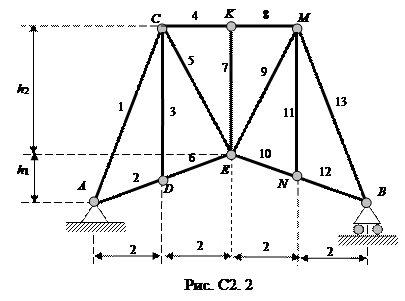
Определить реакции опор фермы от заданной нагрузки, а также усилия в стержнях методом вырезания узлов и методом сечений. Схемы ферм показаны на рис. С2.0 – С2.2. Необходимые для расчета данные приведены в табл. С2.

Таблица С2

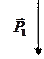
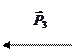
Силы				h 1, м	h 2, м	Номера стержней
Номерусловия	Р 1 = 5кН	Р 2 = 10 кН	Р 3 = 15 кН
Точка приложения силы
	К	С	М			4, 5, 6
	Е	М	С			8, 9, 10
	К	С	М			4, 5, 6
	Е	М	С			8, 9, 10
	К	С	М			4, 5, 6
	Е	М	С			8, 9, 10
	К	С	М			4, 5, 6
	Е	М	С			8, 9, 10
	К	С	М			4, 5, 6
	Е	М	С			8, 9, 10

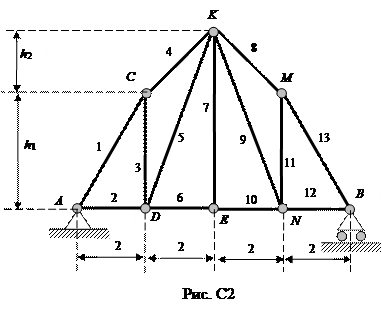
Пример С2. Для фермы, изображенной на рис. С2, определить реакции опор, а также усилия в стержнях 4, 5 6 методом вырезания узлов и методом сечений, если Р ₁ = 5 кН, Р ₂ = 10 кН, Р ₃ = 15 кН, h ₁ = h ₂ = 3 м.

Дата добавления: 2015-06-04