Решение задачи. 1. Расположив оси проекций, как указано на рис

Решение задачи

1. Расположив оси проекций, как указано на рис. 84, найдем модуль равнодействующей системы параллельных сил:
∑ X_i = Р₁ - Р₂ + Р₃ + Р₄ - Р₅ = 10 - 16 + 15 + 8 - 8 = 9,
R = 9 кн.

Таким образом, равнодействующая направлена вправо.

2. Определим расстояние ВО от нижнего конца балансира до линии действия R из уравнения Вариньона (центр моментов в точке В):
-R*BO = -Р₁*BA + Р₂*BC - Р₃*BD - Р₄*BE.
Отсюда
BO = (Р₁*BA - Р₂*BC + Р₃*BD + Р₄*BE)/R = (10*90 - 16*70 + 15*40 + 8*25)/9 = 64,5 см.

Следовательно, линия действия равнодействующей пересекает находящийся в вертикальном положении балансир на расстоянии 64,5 см от нижнего конца В. Здесь (в точке О) и нужно поместить ось балансира

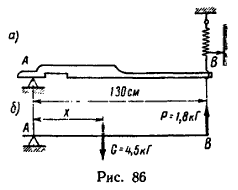
Условие задачи Масса неоднородного стержня составляет 4,5 кг. Для определения положения центра тяжести стержня его левый конец положен на гладкую опору, а правый зацеплен крюком динамометра (рис. 86, а). При горизонтальном положении стержня динамометр показывает усилие 1,8 кГ. Расстояние АВ=130 см от левой опоры до динамометра определено путем непосредственного измерения. Определить положение центра тяжести стержня. << задача 68 || задача 71 >>

1. Рассмотрим стержень как рычаг с опорой в точке А. Кроме реакции опоры, на него действуют две нагрузки: вес G=4,5 кГ (1 кг массы притягивается к земле силой, равной 1 кГ), приложенный в центре тяжести на искомом расстоянии х от опоры А, и усилие пружины динамометра Р=1,8 кГ (рис. 86, б).

2. Составим уравнение равновесия рычага:
∑ M_A(P_i) = 0,

В данном случае относительно точки А моменты создают две силы Р и G:
M_A(P) = +P * AB и M_A(G) = -Gx.

Следовательно,
P * AB - Gx = 0.

Решаем полученное уравнение:
x = P * AB / G = 1,8 * 130 / 4,5 = 52 см.

Центр тяжести стержня расположен на расстоянии 52 см от левой опоры.

Задачу 23 просто решить графическим методом. Для этого нужно начертить в масштабе расположение нитей и, выбрав масштаб для сил (например, 0,2 кГ/мм), построить на векторе G силовой треугольник и, измерив его стороны, найти T_A и T_B (графическое решение рекомендуется выполнить самостоятельно).

Графо-аналитический метод с использованием свойств подобных треугольников целесообразно применять к решению таких задач в том случае, если в схеме конструкции или устройства имеется треугольник, подобный силовому.

Если же в схеме конструкции нет треугольника, подобного силовому, то решение графо-аналитическим методом целесообразнее производить с использованием тригонометрических свойств, потому что при наличии линейных размеров необходимые для решения задачи значения углов, как правило, найти очень просто.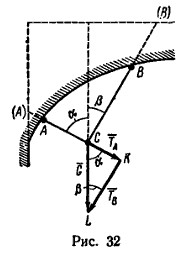

Необходимо отметить, что в задачах, подобных 22 и 23, усилия, вызываемые нагрузкой в стержнях кронштейнов или нитях устройств, удерживающих груз, не зависят от длины этих нитей или стержней.

Допустим, что груз (задача 23) удерживается нитями, прикрепленными не к вертикальной стенке и горизонтальному потолку, как на рис. 30, а к двум точкам криволинейной (сводчатой) поверхности (рис. 32). Но если при этом углы α и β, образуемые нитями CB и CA с вертикалью, остаются такими же, как и на рис. 30, то усилия T_A к T_B не изменяются, хотя сами нити в данном случае становятся короче.

Дата добавления: 2015-06-04