Окружность и круг

Основные формулы

Длина окружности радиуса R вычисляется по формуле:

L = 2πR.

Площадь круга радиуса R вычисляется по формуле:

S = πR² .

Длина l дуги окружности радиуса R вычисляется по формулам:

l = Rα, где α – радианная мера дуги;

,

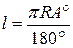где – градусная мера дуги.

Площадь S сектора круга радиуса R, центральный угол которого равен α радиан (А градусов), вычисляется по формулам:

;

.

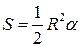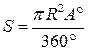Некоторые теоремы об окружностях

28.Угол, вписанный в окружность, измеряется половиной дуги, на которую он опирается.

29. Касательная к окружности перпендикулярна радиусу, проведенному через точку касания.

30. Отрезки двух касательных, проведенных из одной точки окружности равны.

31. Точка касания двух окружностей лежит на линии, соединяющей центры этих окружностей.

32. Если из точки вне окружности проведены к этой окружности секущая и касательная, то произведение секущей на ее внешнюю часть равно квадрату касательной.

Пример 11. Радиус окружности равен 1. Найдите величину острого вписанного угла, опирающегося на хорду, равную .

Решение. Обозначим концы хорды буквами А и В, а центр окружности – О. Найдем α –величину угла АОВ – центрального угла, опирающегося на ту же хорду, что и вписанный угол. По теореме косинусов

АВ² = АО² + ВО² – 2 АО∙ВО∙cosα,

отсюда cosα = – ½. Следовательно, α = 120º. Центральный угол измеряется дугой, на которую опирается, а вписанный угол – половиной дуги, на которую опирается (теорема 28). Значит искомая величина вписанного угла равна 60º.

Ответ: 60º.

Пример 12. Дуга окружности DС, не содержащая точки В, составляет 118º, а дуга окружности ВС, не содержащая точки D, составляет 29º. Найдите вписанный угол DСВ. Решение. Угол DСВ опирается на дугу DВ. Найдем Аº – градусную меру дуги DВ:

Аº = 360º – 118º – 29º = 213º. Тогда по теореме 28 угол DCB равен 213º: 2 = 106,5º, или 106º30¢.

Ответ: 106º30¢.

Пример 13. Угол между хордой DB и касательной ВС к окружности равен 58º. Найдите величину меньшей дуги, стягиваемой хордой DB. Решение. Проведем диаметр ВМ. По теореме 29 ВМ ВС. Следовательно, угол МВD равен

90º – 58º = 32º. Тогда по теореме 28 градусная мера дуги МD составляет 2∙32º = 64º, а значит градусная мера дуги DВ равна 180º – 64º = 116º.

Ответ: 116º.

Пример 14. Три окружности, радиусы которых 60 см, 20 см и 40см, касаются друг друга внешним образом. Найдите радиус окружности, проходящей через центры данных окружностей.

Решение. Обозначим буквами А, В и С центры окружностей. Требуется найти радиус окружности, проходящей через эти точки, т.е. окружности, описанной около треугольника АВС. Из теоремы 31 следует, что расстояние между центрами касающихся окружностей равно сумме длин их радиусов. Таким образом, АВ = 80 см, ВС = 60 см, а АС = 100 см. Вычислим площадь треугольника АВС по формуле Герона: .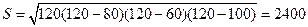

Площадь треугольника АВС можно также вычислить по формуле .

Решая уравнение , получим, что R = 50.

Ответ: 50 см.

Дата добавления: 2015-06-04