Шар, сфера

Конус

Введем следующие обозначения:

R – радиус основания конуса, H – высота конуса, l – образующая конуса, V – объем конуса, S_бок. – площадь боковой поверхности конуса.

Основные формулы:

S_бок. = pR l; V = 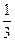pR²H.

Пример 7. В основании правильной четырехугольной пирамиды лежит квадрат со стороной равной 3, а высота ее равна 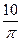. Найдите объем конуса, описанного около пирамиды.

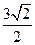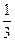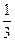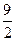
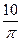Решение. Основанием конуса является круг, в который вписан квадрат, лежащий в основании призмы. Радиус этого круга равен половине диагонали квадрата: R = . Следовательно, объем конуса V = pR²H = p = 15.

Ответ: 15.

Пример 8. Площадь боковой поверхности конуса равна 15p. Радиус его основания равен 3. Найдите высоту конуса.

Решение. По формуле для вычисления площади боковой поверхности конуса pR l = 15p. Откуда следует, что образующая конуса l = 5. Высоту конуса найдем по теореме Пифагора: 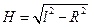= 4.

Ответ: 4.

Введем следующие обозначения:

R – радиус шара, S – площадь сферической поверхности (площадь поверхности шара), V – объем шара, h – высота шарового сегмента, S_сегм. – площадь сферической части поверхности сегмента, V_сект. – объем шарового сектора.

Основные формулы:

.

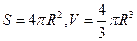S_сегм. = 2pRh

V_сект. =

Пример 9. Площадь поверхности одного шара в 16 раз больше площади поверхности другого шара. Во сколько раз объем первого шара больше объема второго шара?

Решение. Обозначим буквами R₁ и R₂ радиусы первого и второго шаров соответственно, а буквами S₁ и S₂ – площади поверхностей этих шаров. Тогда S₁ = 16S₂, отсюда следует, что

R₁² = 16R₂², R₁ = 4R₂. Тогда

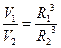= 64.

Ответ: 64.

Тренировочные задания

1) [4] Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 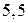. Найдите объем параллелепипеда.

(Отв. 665,5).

2) [4] В цилиндрический сосуд налили 2100 см³ воды. Уровень воды при этом достиг высоты 20 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 5 см. Чему равен объем детали?

(Отв. 525 см³).

3) [4] В сосуд, имеющий форму правильной треугольной призмы, налили 1900 см³ воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 20 см до отметки 22 см. Найдите объем детали.

(Отв. 190 см³).

4) [4] В основании прямой призмы лежит прямоугольный треугольник с катетами 10 и 9. Боковые ребра равны 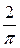. Найдите объем цилиндра, описанного около этой призмы.

(Отв. 90,5).

5) [4] Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 40.

(Отв. 120).

6) [4] Объем конуса равен 48. Через середину высоты параллельно основанию конуса проведено сечение, которе является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

(Отв. 6).

7) [4] Диагональ куба равна 3. Найдите площадь его поверхности.

(Отв. 18).

8) [4] Найдите объем параллелепипеда 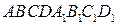, если объем треугольной пирамиды равен 3.

(Отв. 18).

9) [4] Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду?

(Отв. 2).

10) [4] Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 3 раза?

(Отв. 3).

11) [9] Бильярдный шар весит 360 г. Сколько граммов весит шар вдвое меньшего радиуса, сделанный из того же материала?

(Отв. 45).

Дата добавления: 2015-06-04