Геометрична оптика

3.1. Закони геометричної оптики. Абсолютний та відносний показники заломлення. Хід світлових променів з менш оптично густого середовища в більш оптично густе й навпаки. Явище повного внутрішнього відбивання.

3.2. Принцип Ферма. Закони геометричної оптики як наслідок принципу Ферма.

3.3. Центровані оптичні системи. Тонкі лінзи. Типи лінз. Фокусна відстань лінзи. Оптична сила лінзи. Побудова зображень за допомогою лінз. Формула тонкої лінзи. Правила знаків.

3.4. Оптичні призми.

3.5. Око як оптична система. Будова ока. Акомодація ока. Корекція дефектів зору. Адаптація ока. Спектральна чутливість ока. Роздільна здатність ока. Бінокулярний зір.

3.1. Геометрична оптика заснована на деяких положеннях, які спочатку були встановленні як експериментальні закони. Розглянемо ці закони:

1) закон прямолінійного поширення світла – в однорідному прозорому середовищі світло поширюється прямолінійно;

2) закон незалежності поширення світлових променів – світлові промені, які поширюються в просторі, під час перетину не впливають один на одного;

3) закон оборотності світлових променів – якщо світловий промінь поширюється з точки 1 в точку 2, то в зворотному напрямі з точки 2 в точку 1 він поширюється по тому самому шляху;

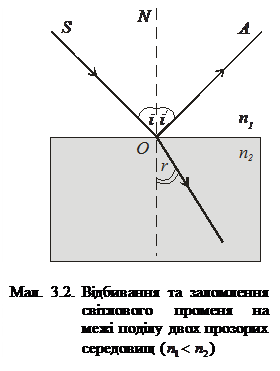
4) закон відбивання світла – промінь падаючий, промінь відбитий і пер­пендикуляр, поставлений в точку падін 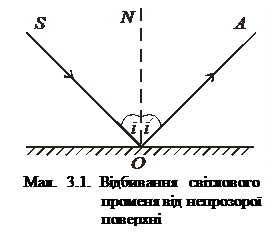ня, лежать в одній площині; при цьому кут падіння дорівнює куту відбивання: 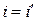(мал. 3.1). Кут між падаючим променем (SO) і перпендикуляром (NO) у точку падіння називають кутом падіння (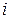). Кут між відбитим променем (OA) і перпендикуляром (NO) у точку падіння називають кутом відбивання (NO) називають кутом відбивання ().

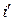5) закон заломлення світла – промінь падаючий, промінь заломлений і
перпендикуляр, поставлений в точку падіння, лежать в одній площині; при цьому для будь-якого кута падіння відношення синуса кута падіння до синуса кута заломлення є величина стала для двох певних середовищ і називається відносним показником заломлення (мал. 3.2):

.

Кут між заломленим променем (OB) і продовженням перпендикуляра (NO) в точку падіння називають кутом заломлення ().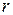

Усі прозорі середовища характеризуються абсолютним показником заломлення. Абсолютним показником заломлення називають відношення синуса кута падіння до синуса кута заломлення, коли падаючий промінь йде із вакууму або із повітря в дане середовище. Абсолютний показник заломлення вакууму дорівнює одиниці (). Показник заломлення повітря вважають таким, що дорівнює одиниці, хоч його більш точне значення при нормальних умовах .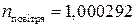

Позначимо абсолютний показник заломлення першого середовища 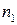, а другого ‑ 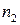. Тоді відносний показник заломлення 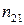дорівнює відношенню абсолютних показників заломлення: .

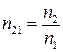З теорії електромагнітного поля випливає, що абсолютний показник заломлення є числом, яке показує в скільки разів швидкість світла у вакуумі (с) більша за швидкість світла в даному середовищі (v):

.

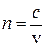Якщо 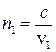, , 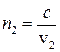то закон заломлення можна подати у вигляді:

.

Абсолютний показник заломлення залежить від частоти (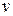) або від дов­жини (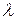) світлової електромагнітної хвилі Для вакууму частота й довжина хвилі зв’язані між собою співвідношенням: 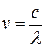. Різним частотам, або довжинам хвиль відповідають різні показники заломлення. Залежність показника заломлення від довжини (частоти) хвилі називають дисперсією. Розрізняють нормальну дисперсію ( 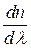< 0), коли із збільшенням довжини хвилі показник заломлення зменшується і аномальну дисперсію ( 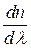> 0), коли із збільшенням довжини хвилі показник заломлення збільшується.

Середовище, що характеризується більшим показником заломлення, називають більш оптично густим. Промінь світла, що проходить з менш оптично густого середовища в більш оптично густе середовище, наближається

а) б)

Мал. 3.3. Хід світлового променя через межу поділу двох прозорих середовищ ()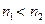

до перпендикуляра, поставленого в точку падіння (мал. 3.3,а). На основі закону оборотності світлових променів промінь, що йде з більш оптично густого середовища в менш оптично густе, відхиляється від перпендикуляра, поставленого в точку падіння (мал. 3.3,б).

Коли світло поширюється з більш оптично густого середовища в менш оптично густе, то на межі їхнього поділу відбувається перерозподіл світлових потоків у залежності від кута падіння. Розглянемо окремі випадки (мал. 3.4). Якщо кут падіння дорівнює нулю (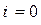), то світловий промінь (1) без заломлення проходить з одного середовища в інше. Для деякого кута падіння (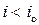) світловий промінь на межі поділу двох середовищ поділяється на відбитий (2) та заломлений (3). Для будь-якої пари прозорих середовищ завжди існує певний кут падіння 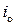при якому кут заломлення 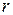досягає максимального значення й заломлений промінь (4) ковзає по межі поділу двох середовищ.

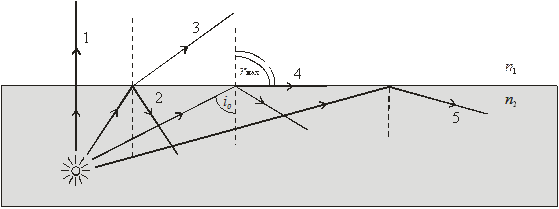
Мал. 3.4. Хід світлових променів з більш оптично густого середовище в менш
оптично густе ()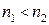

Такий кут падіння називають граничним кутом повного внутрішнього відбивання. Якщо кут падіння перевищуватиме кут 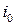(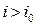), то заломлення світлового променя не відбувається й відбитий промінь (5) повністю залишається в більш оптично густому середовищі. Таке явище називають повним внутрішнім відбиванням. Граничний кут повного внутрішнього відбивання для даних середовищ знаходиться за допомогою закону заломлення. Якщ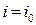о , то 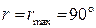. Тоді . Звідки .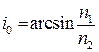

3.2. Деякі задачі геометричної оптики зручно розв’язувати, користуючись принципом Ферма, який був сформульований в 1660 році французьким математиком Ферма: світло поширюється по такому шляху, на подолання якого йому необхідний мінімальний час.

Нехай світло поширюється в середовищі з показником заломлення n. Тоді швидкість світла в цьому середовищі дорівнює: v 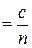, де c швидкість світла у вакуумі. Час, протягом якого світло проходить деяку відстань S у середовищі з показником заломлення n, визначається співвідношенням:

,

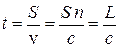де S геометрична довжина шляху, 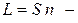оптична довжина шляху. Отже, оптичною довжиною шляху називають добуток геометричної довжини шляху на показник заломлення середовища, в якому поширюється світловий промінь.

Нехай світло проходить кілька середовищ з показниками заломлення (мал. 3.5). З точки А світло потрапляє в точку В шляхом АМNB, 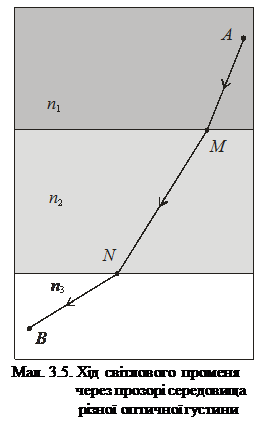для подолання якого час

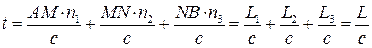
повинен мати найменше значення. Оскільки швидкість світла у вакуумі є величина стала, то принцип Ферма можна сформулювати так: світло поширюється по такому шляху, оптична довжина якого є мінімальною.

Виявляється, що чотири закони геометричної оптики є наслідком принципу Ферма: закон прямолінійного поширення світла оскільки мінімальний оптичний шлях між двома точками середовища являє собою пряму, то в однорідному прозорому середовищі світло поширюється прямолінійно; закон оборотності світлових променів оптичний шлях, який є мінімальним під час поширення світла з точки 1 в точку 2, буде мінімальним й під час поширення світла з точки 2 в точку 1.

Одержимо за допомогою принципу Ферма закон відбивання світла. Нехай світло поширюється в однорідному прозорому середовищі від точки А до точки В, відбиваючись від плоскої поверхні MN в точці О (мал. 3.6). Спочатку продовжимо пряму ОА та зафіксуємо на ній в будь-якому місці точку В'. З точки В' проводимо перпендикуляр до поверхні MN (точка С). На продовженні цього перпендикуляра треба відкласти відрізок СВ, причому СВ=СВ'. Відрізок СВ обмежується точкою В, в яку і потрапляє світловий промінь з точки А. Отже, точки В' і В є симетричними. Сполучимо точки В і О. Від точки О поставимо перпендикуляр ОК до поверхні MN. Трикутник ВОВ' є рівнобедреним, тому ОВ' = ОВ.

Визначимо на поверхні MN положення іншої точки О', яку треба з’єднати з точками А, В і В'. Трикутник ВО'В' є також рівнобедреним, тому ВО' = О'В. Тоді довжини шляхів від точки А до точки В записуються так:

АО + ОВ = АО + О'В', АО' + О'В = АО' + О'В'.

Лінія АОВ' є прямою, лінія АО'В' є ламаною при будь-якому положенні точки О'. Оскільки будь-яка ламана завжди більша за пряму між тими самими точками, то тоді маємо:

АО + ОВ < АО' + О'В.

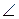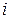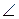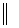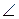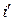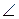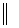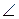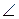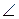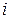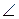Отже, геометричний та оптичний шлях АОВ є найменшим. При цьому АОК () = ОВ'С,томущо ОК ВВ', АВ' – січна. КОВ () = ОВС, оскільки ОК СВ, ОВ – січна. Але ОВС = ОВ'С, тому що трикутник ВОВ' є рівнобедреним. Тому АОК () = КОВ (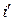). Таким чином, кут падіння дорівнює куту відбивання .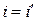

Одержимо за допомогою принципу Ферма закон заломлення світла. Нехай світловий промінь поширюється з менш оптично густого середовища (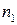) від точки А в більш оптично густе середовище (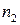) до точки В (мал. 3.7). Для будь-якого променя оптична довжина шляху дорівнює:

.

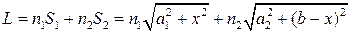Щоб знайти мінімальне значення оптичної довжини шляху, знайдемо першу похідну від L по x та прирівняємо її до нуля:

.

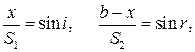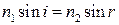Оскільки то або .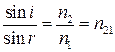

3.3. Оптичною системою називають пристрій, який формує дійсне оптичне зображення об’єкта або перетворює світловий потік. Оптична система складається з лінз, призм, прозорих пластинок, дзеркал тощо, скомбінованих між собою так, щоб одержувати оптичне зображення об’єкта або перетворювати світловий потік. У загальному випадку оптичні системи мають дві й більше заломлюючих поверхонь. Практичного значення набули системи, для яких центри кривизни всіх заломлюючих поверхонь лежать на одній прямій. Оптичні системи, що мають таку властивість називають центрованими. Пряму лінію, на якій лежать центри кривизни заломлюючих поверхонь оптичної системи, називають головною оптичною віссю оптичної системи.

До найпростіших центрованих систем відноситься лінза. Вона складається з двох заломлюючих поверхонь, які обмежують прозору речовину, наприклад, скло. Одна із заломлюючих поверхонь обов’язково повинна бути сферичною, друга – або сферичною, або плоскою (мал. 3.8). У залежності від комбінації заломлюючих повер 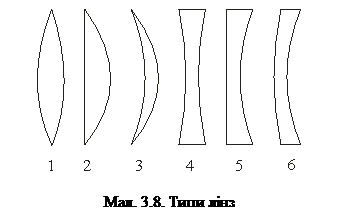хонь лінзи можуть бути: двоопуклі (1), плоско-опуклі (2), вгнуто-опуклі (3),
двовгнуті (4), плоско-вгнуті (5), опукло-вгнуті (6). При цьому лінзи 1-3 є збірними, лінзи 4-6 є розсіюючими, якщо матеріал, з якого вони виготовлені, є більш оптично густим, ніж навколишнє

середовище.

Розглянемо двоопуклу лінзу (мал. 3.9). Лінзу називають тонкою, якщо її товщина АВ досить мала в порівнянні з радіусами кривизни 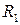і 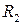заломлюю 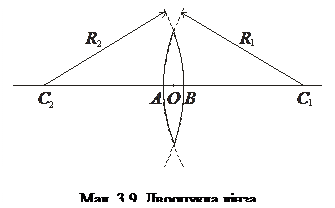чих поверхонь. При цьому вважається, що вершини цих поверхонь А і В зливаються в точку О, яку називають оптичним центром лінзи. Будь-яка пряма, що проходить через оптичний центр лінзи, називається оптичною віссю лінзи. Оптична вісь , яка проходить через центри кривизни і заломлюючих поверхонь та оптичний центр лінзи, називається головною оптичною віссю лінзи.

Промені, які є паралельними до головної оптичної осі, заломлюються в збірній лінзі й перетинаються в точці F, яка лежить на цієї осі й називається фокусом лінзи (мал. 3.10,а). Для розсіюючої лінзи фокусом є точка на головній оптичній осі, в якій перетинаються не самі промені, а їх уявні продовження в бік, що протилежний напрямку поширення світла (мал. 3.10,б). Відстань від фокусу лінзи до її оптичного центру називають фокусною відстанню (f). Площина, яка перпендикулярна до головної оптичної осі й проходить через фокус лінзи, називається фокальною площиною.

Мал. 3.10. Хід світлових променів через тонку лінзу:

а) збірна лінза; б) розсіююча лінза

Фокусна відстань лінзи може бути розрахована за формулою:

де 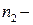показник заломлення матеріалу, з якого виготовлена лінза; 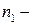показник заломлення середовища, що оточує лінзу; 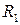і радіуси кривизни заломлюючих сферичних поверхонь.

Відповідно до типу лінз формулу (1) записують згідно правила знаків: якщо заломлююча поверхня знаходиться ліворуч від центру кривизни, то радіус кривизни цієї поверхні є додатним; якщо заломлююча поверхня знаходиться праворуч від центру кривизни, то радіус кривизни цієї поверхні є від’ємним. Розглянемо приклади:

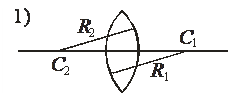для двоопуклої лінзи 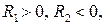тому формула (3.1) набуває вигляду:

для двовгнутої лінзи 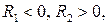тому формула (3.1) набуває вигляду:

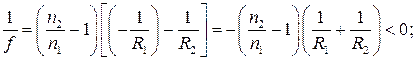
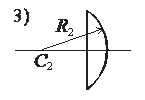для плоско-опуклої лінзи 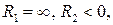тому формула (3.1) набуває вигляду:

для плоско-вгнутої лінзи 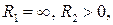тому формула (3.1) набуває вигляду:

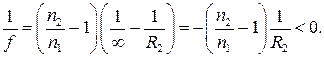
Величина, яка є оберненою до фокусної відстані, називається оптичною силою лінзи:

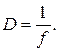
Оптична сила визначає збірну або розсіюючу здатність лінзи. У системі СI оптична сила вимірюється в діоптріях (дптр). Оптичну силу в 1 діоптрію має лінза з фокусною відстанню 1м. Оптична сила збірних лінз є додатною, розсіюючих лінз – від’ємною. Оптична сила оптичної системи, яка складається з кількох лінз, дорівнює алгебраїчній сумі оптичних сил цих лінз. Наприклад, оптична система з двох збірних лінз має більшу оптичну силу й меншу фокусну відстань, ніж кожна з них окремо.

Оптичні зображення предметів, які можна дістати за допомогою лінз, поділяються на дійсні та уявні. Дійсні зображення створюються збіжними пучками променів у точках, де вони перетинаються. Дійсні зображення можна спостерігати на екрані або фотоплівці, які знаходяться в точках перетину променів. Якщо промені, що виходять з оптичної системи, розходяться, то подумки їх можна продовжити в протилежному напрямку, де вони перетинаються. Точку перетину цих променів називають уявним зображенням точки предмета. Сукупність таких точок складають уявне зображення предмета. Уявне зображення неможливо одержати на екрані або зафіксувати на фотоплівці, але інша оптична система (збірна лінза, око людини) здатна перетворити уявне зображення на дійсне.

Тонкі лінзи дають неспотворені зображення предметів, якщо падаюче світло є монохроматичним, а розміри предметів є малими в порівнянні з відстанями від предметів до лінз. Для побудови зображень предметів за допомогою тонких лінз досить використати два промені: перший промінь йде від крайньої точки предмета паралельно головній оптичній осі й після заломлення в лінзі він перетинає фокус; другий промінь йде від тієї самої точки предмета через оптичний центр лінзи без зміни напрямку. Розглянемо приклади.

1. Предмет АВ знаходиться за подвійним фокусом лінзи:

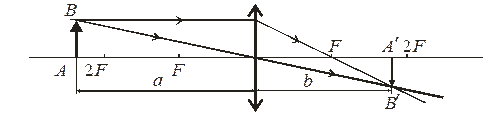
Зображення А'В' є дійсним, оберненим й зменшеним (а – відстань від предмета до лінзи, b – відстань від лінзи до зображення).

2. Предмет АВ знаходиться на подвійному фокусі лінзи:

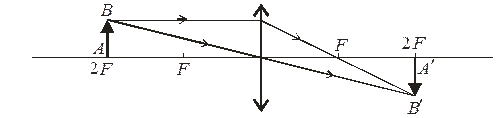
Зображення А'В' є дійсним, оберненим й таким самим за розміром, як предмет АВ.

3. Предмет АВ знаходиться між фокусом та подвійним фокусом лінзи:

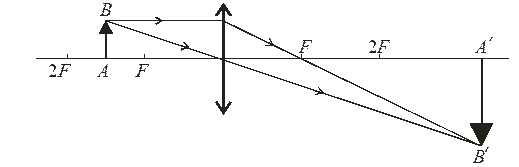
Зображення А'В' є дійсним, оберненим й збільшеним. 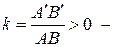збільшення лінзи.

4. Предмет АВ знаходиться у фокусі лінзи:

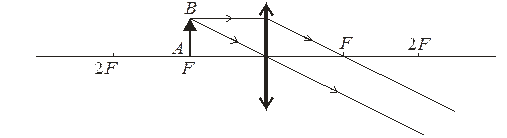
Зображення відсутнє, оскільки після лінзи промені є паралельними.

5. Предмет АВ знаходиться між фокусом лінзи та самою лінзою:

Зображення А'В' є уявним, прямим й збільшеним.

6. Предмет АВ знаходиться між фокусом та подвійним фокусом лінзи:

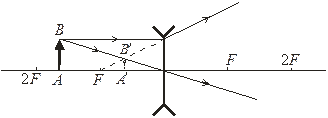
Для будь-якого положення предмета АВ його зображення А'В' буде уявним, прямим й зменшеним.

Формулою тонкої лінзи називають рівняння вигляду:

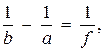
яку для кожного конкретного випадку треба записувати відповідно до правила знаків: відстань від оптичного центру лінзи за напрямком поширення променів є додатною; відстань від оптичного центру лінзи проти напрямку поширення променів є від’ємною. Для збірної лінзи фокусна відстань є додатною, для розсіювальної лінзи – від’ємною.

Для побудов 1, 2, 3 відстані 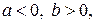тому формула тонкої лінзи набуває вигляду:

.

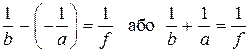Для побудови 4 відстані 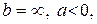тому формула тонкої лінзи набуває вигляду:

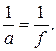
Для побудови 5 відстані тому формула тонкої лінзи набуває вигляду:

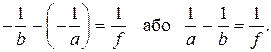
Для побудови 6 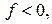тому формула тонкої лінзи набуває вигляду:

3.4. Оптичні призми є складовою частиною оптичних систем. Вони виготовляються з матеріалів, які є прозорими для електромагнітних хвиль оптичного діапазону, а їх зовнішній вигляд досить часто не відповідає математичному поняттю призми. Оптичні призми поділяють на три класи: спектральні, відбиваючи й поляризаційні. Поляризаційні призми вивчатимуться в розділі хвильової оптики, який стосується поляризованого світла.

Спектральні призми просторово розділяють електромагнітні хвилі за довжиною хвилі. Таке розділення білого світла на монохроматичні складові є результатом явища дисперсії. Для видимого діапазону такі призми виготовляють із скла, для ультрафіолетової області – із кварцу, для інфрачервоної області – із фтористого літію, хлористого магнію. Розглянемо деякі типи спектральних призм:

1) тригранна призма (мал. 3.11). Бокові грані цієї призми утворюють між собою кут g, який називають заломлюючим 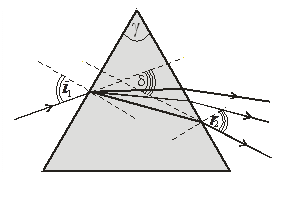кутом. Для призм цього класу він дорівнює 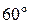. Якщо на призму падає біле світло, то поза призмою спостерігається спектр. Спектром називають залежність інтенсивності світла від довжини (частоти) хвилі. Кут відхилу променів d можна визначити за допомогою формули ;

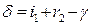2) призма Аббе. Для цієї призми розкладання білого світла на спектр 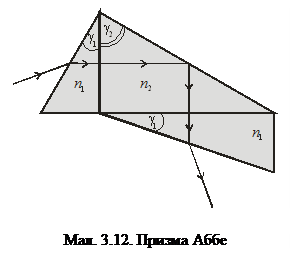супроводжується відхилом світлового пучка на кут 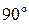(мал. 3.12). Призма складається з двох прямокутних призм із заломлюючим кутом 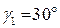та прямокутної, відбиваючої призми із заломлюючим кутом .

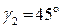Показники заломлення призм є однаковими ;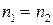

3) призма Амічі є призмою прямого ходу (мал. 3.13).Вона складається із трьох або більшої кількості прямокутних призм. Бокові призми виготовляються із скла (крон) з меншим показником заломлення 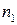, а центральна призма із скла (флінт) з більшим показником заломлення ().

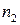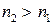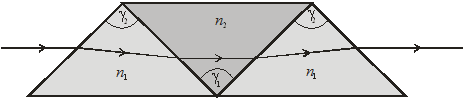
Мал. 3.13. Призма Амічі

Середній промінь спектра проходить призму Амічі без відхилу, а інші промені, що мають більшу або меншу довжину хвилі, відхиляються від середнього променя по обидві сторони.

Відбиваючі призми використовують для зміни напрямку поширення світлового пучка, зменшення геометричних розмірів оптичних приладів, повернення зображення предметів. На відміну від спектральних призм відбиваючі призми просторово не розділяють світлові промені в залежності від довжини хвилі. Відбивання світлових променів від граней призми є повним внутрішнім відбиванням, тобто грані призми перетворюються на ніби дзеркальні. Існує залежність між кількістю відбиваючих граней й повертанням зображення предмету: якщо відбивання світлових променів відбувається в однієї площині, то призма з парною кількістю відбиваючих граней дає пряме зображення предмету; призма з непарною кількістю відбиваючих граней дає обернене зображення предмету. Для різних ділянок оптичного діапазону відбиваючі призми виготовляють з тих самих матеріалів, що й спектральні призми. Розглянемо деякі типи відбиваючих призм:

1) тригранна прямокутна рівнобедрена призма може відбивати світлові промені як від гіпотенузи (мал. 3.14,а), так й від катетів (мал. 3.14,б). У випадку (а) вона змінює напрям ходу променів на кут 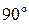й повертає зображення предмета (одна відбиваюча грань). У випадку (б) вона змінює напрям ходу променів на кут 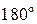, але зображення залишається прямим (дві відбиваючих грані);

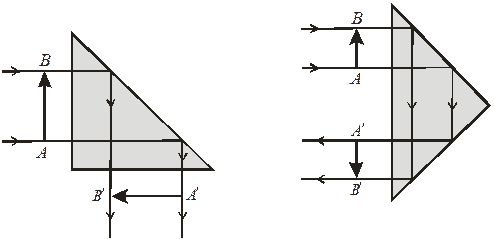
а) б)

Мал. 3.14. Тригранна прямокутна рівнобедрена призма

2) прима Дове є призмою прямого зору (мал. 3.15). Вона зберігає напрям ходу світлових променів й повертає зображення предмета (одна відбиваюча грань);

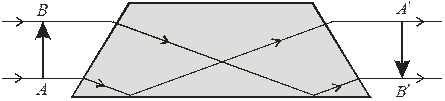
Мал. 3.15. Призма Дове

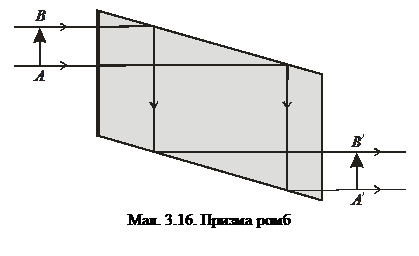3) призма ромб (мал. 3.16) зберігає напрям ходу світлових променів й дає пряме зображення предмета (дві відбиваючих грані);

4) пентапризма (мал. 3.17) змінює напрям ходу променів на кут 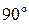й дає пряме зображення предмета (дві відбиваючих грані).

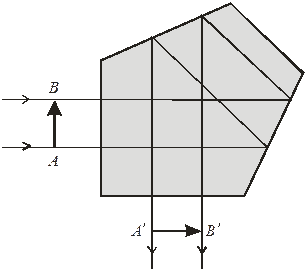
Мал. 3.17. Пентапризма

Дата добавления: 2015-06-04