Метод координат

Пример 15. Найдите площадь четырехугольника, вершины которого имеют координаты (2;3), (2;7), (9;0), (9;4).

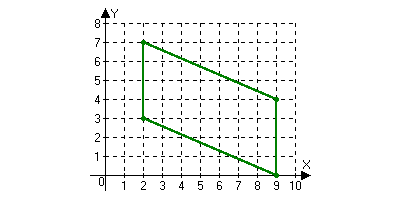
Решение. Данный четырехугольник является параллелограммом. В качестве основания параллелограмма возьмем сторону параллельную оси ординат. Ее длина равна 4. Тогда длина высоты, опущенной на основание, равна 7. Площадь параллелограмма равна 7×4 = 28.

Ответ: 28.

Пример 16.

Найдите площадь треугольника, вершины которого имеют координаты А(2;3), В(6;9), С(8;2).

Решение.

Рассмотрим прямоугольник с вершинами М(2;2), N(2;9), P(8;9) и C(8;2). Его площадь равна произведению длин сторон MN и MC: 6×7 = 42. Вычислим площади треугольников ANB, BPC и MAC: S_ANB = ½ AN×NB = 12, S_BPC = ½ BP×BC = 7, S_MAC = ½ MA×MC = 3. Вычтем из площади прямоугольника MNPC площади треугольников ANB, BPC и MAC и, тем самым найдем площадь треугольника АВС: 42 – 12 – 7 – 3 = 20.

Ответ: 20.

Тренировочные задания

1) [2] В треугольнике длины сторон рвны 3, 5, n, где n – натуральное число. Укажите возможные значения n.

(Отв. 3, 4, 5, 6, 7).

2) [2] В равнобедренной трапеции диагональ составляет с боковой стороной угол 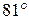. Боковая сторона равна меньшему основанию. Найти острый угол трапеции.

(Отв. ).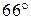

3) [2] Около окружности описана равнобедренная трапеция с боковой стороной, равной 10. найти среднюю линию трапеции.

(Отв. ).

4) [2] Найти высоту прямоугольного треугольника, опущенную на гипотенузу, если эта высота делит гипотенузу на отрезки, равные 3 и 12.

(Отв. ).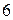

5) [2] Найти гипотенузу прямоугольного треугольника, если радиус описанной около этого треугольника окружности равен 4.

(Отв. ).

6) Отношение периметров двух ромбов с равными острыми углами равно 3. Найдите отношение площадей этих ромбов.

(Отв. 9).

7) Найти площадь ромба, если длина одной из его диагоналей равна 12, а длина другой на 25% больше.

(Отв. 90).

8) Найти длину дуги в 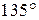, если радиус окружности равен 3.

(Отв. ).

9) [2] Найти радиус описанной около треугольника окружности, если его сторона, равная 4, лежит против угла в .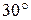

(Отв. ).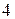

10) [2] В параллелограмме угол между высотами, проведенными из вершины тупого угла, равен . Найти тупой угол параллелограмма.

(Отв. ).

11) Вписанный треугольник разбивает окружность на дуги, длины которых равны 120, 280 и 320. Найдите наибольший угол треугольника.

(Отв. ).

12) [2] Биссектриса угла А параллелограмма ABCD делит сторону BC на отрезки BK = 49 и

KC = 81. Найти периметр параллелограмма.

(Отв. ).

13) [4] Один из углов равнобедренного треугольника равен . Найдите другие углы треугольника.

(Отв. ).

14) [4] Один из углов равнобедренного треугольника на 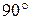больше другого. Найдите меньший угол треугольника.

(Отв. ).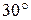

15) [4] В треугольнике ABC AD – биссектриса, угол C равен , угол CAD равен 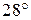. Найдите угол B.

(Отв. ).

16) [4] Найдите острый угол между биссектрисами острых углов прямоугольного треугольника.

(Отв. ).

17) [4] В треугольнике ABC угол A равен 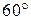, угол В равен . AD, BE и СF – биссектрисы, пересекающиеся в точке О. Найдите угол AОF.

(Отв. ).

18) [4] В прямоугольнике диагональ делит угол в отношении . Меньшая сторона прямоугольника равна 6. Найти диагональ данного прямоугольника.

(Отв. ).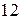

19) [4] Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.

(Отв. ).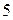

20) [4] Найдите площадь четырехугольника, вершины которого имеют координаты .

(Отв. ).

Дата добавления: 2015-06-04