Распределение Бозе – Эйнштейна

Идеальный газ из бозонов (бозе–газ) – описывается квантовой статистикой Бозе –Эйнштейна.

Распределение Бозе–Эйнштейна – закон, выражающий распределение частиц по энергетическим состояниям в бозе–газе: при статистическом равновесии и отсутствии взаимодействия среднее число частиц в i - ом состоянии с энергией Е_i при температуре системы Т равно

_Б-Э = , где

k – постоянная Больцмана,

T – термодинамическая температура,

μ – химический потенциал – термодинамическая функция состояния, определяющая изменение внутренней энергии системы.

Одним из условий термодинамического равновесия системы является равенство химического потенциала для всех частей системы.

Для систем бозонов с постоянным числом частиц химический потенциал может принимать только отрицательные значения (μ < 0).

Величину называют также числом заполнения энергетического уровня с энергией Е_i (далее будем для краткости писать просто Е).

Из анализа распределения Б – Э следует, что число бозонов, находящихся на одном энергетическом уровне (в одном состоянии), ничем не ограничено и при малых значениях параметра 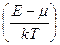может оказаться очень большим, а при Е = 0 в системе бозонов может происходить бозе – конденсация, с которой связаны такие явления, как сверхпроводимость и сверхтекучесть.

Рассмотрим случай малых чисел заполнения (будем считать

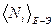<< 1). Это условие выполняется при >> 1 или при >> 1. Тогда можно записать

, где .

Отсюда следует, что при малых числах заполнения, или, как говорят, в случае разреженного газа бозонов распределения Б – Э переходит в классическое распределение Максвелла – Больцмана.

< N>

I – статистическое распределение Максвелла – Больцмана;

II –статистическое распределение Бозе – Эйнштейна

Газ, свойства которого в силу тождественности частиц в квантовой механике отличаются от свойств классического идеального газа, называется вырожденным газом.

Газ бозонов является вырожденным. Только в случае, когда 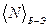<< 1, вырождение снимается и разреженный бозе–газ ведёт себя подобно классическому газу.

Обычные газы, атомы которых являются бозонами, при нормальных температурах и давлениях не являются вырожденными и подчиняются классической статистике. Вырождение для них наступает либо при очень низких температурах, либо при очень высоких давлениях, т.е. тогда, когда эти газы перестают быть идеальными.

С помощью распределения Бозе–Эйнштейна описываются свойства теплового излучения, теплоёмкость кристаллов и многие другие физические явления.

Для систем бозонов с переменным числом частиц химический потенциал равен нулю (μ = 0). Распределение Бозе–Эйнштейна для систем с переменным числом частиц принимает вид

.

Пример: пользуясь распределением Б – Э можно получить формулу

Планка для равновесного излучения.

Рассмотрим излучение, находящееся внутри замкнутой полости, стенки

которой нагреты до комнатной температуры Т. Это излучение представляет собой идеальный газ фотонов, т.е. систему бозонов с переменным числом частиц, распределение по энергиям которых с учётом того, что описывается выражением

Плотность квантовых состояний g(E), т.е. число состояний приходящихся на единичный энергетический интервал, для фотонов описывается выражением

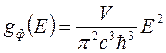, где

V – объём полости; с – скорость света в вакууме; Е/с – импульс фотонов

(по аналогии с плотностью квантовых состояний 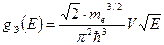для нерелятивистских электронов с импульсом )

Энергия излучения в узком энергетическом интервале от Е до (Е+dE) складывается из энергий отдельных фотонов и равна

< N_ф>^.g_ф (E)^. E ^. dE

В частотном интервале, соответствующему данному энергетическому интервалу

от до

можно получить выражение для той же самой энергии с помощью объёмной спектральной плотности энергии излучения и_ω,Т, представляющей собой энергию излучения в одиночном частотном интервале, отнесённую к единице объёма

u_ω,T^..V^.dω = <N_ф>g_ф(E)E^.dE.

Тогда, заменив dE на 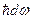и Е на 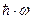получим

.

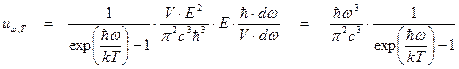Дата добавления: 2015-06-04