Динамическая система

Динамический элемент системы

Динамический элемент характеризуется тем, что его выход в любой момент времени tзависит не только от входа в настоящий момент t, но и от значений входа и, быть может, выхода в прошлые моменты времени t-1, t - 2,...

Например, в статической форме линейная связь между национальным доходом N и потреблением С в любой год t может быть представлена в форме (индекс времени t опушен, но подразумевает­ся по умолчанию):

С = aN (статический элемент),

где а — доля фонда потребления в национальном доходе.

В динамике эта связь может быть представлена в виде:

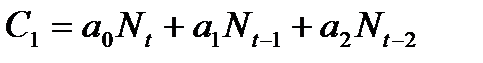(динамический элемент),

т.е. потребление в текущий год t зависит от величины национального дохода не только в настоящий год t, но и в предшествующие годы t-1, t-2.

Таким образом, в динамическом элементе причина переходит в следствие не мгновенно, а с некоторым запозданием.

Система называется динамической, если в ее составе имеется хотя бы один динамический элемент.

Пример 1.1. Экономика в форме модели Солоу как динамическая система. В модели Солоу экономика рассматривается как замкну­тое единое неструктурированное целое, производит один универ­сальный продукт, который может как потребляться, так и инве­стироваться.

В этой модели рассматривается пять макроэкономических пока­зателей (эндогенных переменных):

Y— валовой внутренний продукт (ВВП);

I — валовые инвестиции;

С — фонд потребления;

К— основные производственные фонды;

L — число занятых в производственной сфере.

Первые три переменные (Y,I,C) являются показателями типа потока (их значения накапливаются в течение года), переменные K, L — мгновенные переменные (их значения могут быть измерены, вообще говоря, в любой момент непрерывного времени).

Модель Солоу с дискретным временем. Модель Солоу с дискрет­ным временем задается системой уравнений вида:

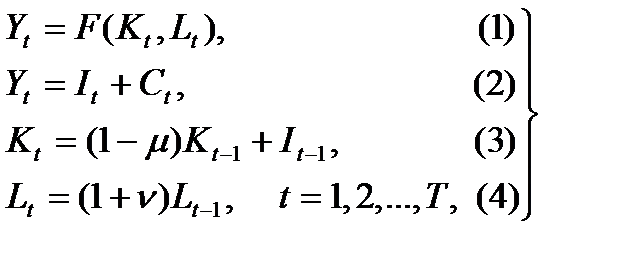(1.1.1)

где t = 0 — базовый год;

t=T — конечный год изучаемого периода;

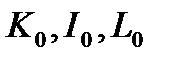считаются заданными.

С содержательной точки зрения эти уравнения имеют следую­щий смысл. Первое уравнение задает ВВП как производственную функцию от ресурсов — основных производственных фондов и числа занятых, второе уравнение — распределение ВВП на валовые инвестиции и потребление. Третье уравнение — это рекуррентное соотношение для определения ОПФ будущего года по значениям ОПФ и инвестиций текущего года. В этом уравнении µ — коэффи­циент выбытия (износа) ОПФ в расчете на год. Данный коэффици­ент предполагается постоянным. Из уравнения видно, что инвести­ции, сделанные в текущем году, материализуются в фонды в будущем году, т.е. лаг капиталовложений равен одному году. Четвертое урав­нение — это рекуррентное соотношение для определения числа за­нятых в будущем году на основании числа занятых в текущем году. Как видим, данное уравнение основано на гипотезе постоянства го­дового темпа прироста числа занятых ν.

С точки зрения классификации элементов на статические и ди­намические, уравнения (1.1.1) (каждое из которых является форма­лизованной записью элемента) могут быть истолкованы следующим образом. Первое уравнение задает нелинейный статический элемент (вход — 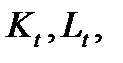выход — 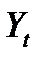), второе уравнение — линейный статиче­ский элемент (вход — 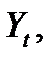выход — 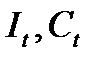), третье уравнение — ли­нейный динамический элемент (вход — 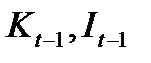, выход — 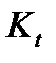), чет­вертое уравнение — линейный динамический элемент (вход — 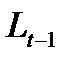, выход — ).

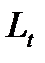Таким образом, экономика в форме модели Солоу, видимым образом неструктурированная, на самом деле структурируется в контур с обратной связью, показанный на рис. 1.2. Тем самым эко­номика в форме модели Солоу является динамической системой, по­скольку в ее составе имеются динамические элементы.

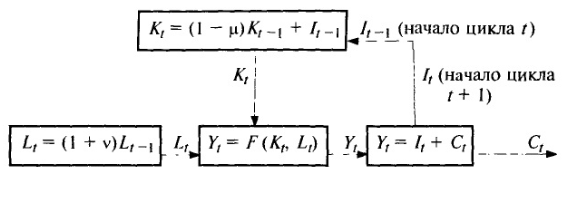
Рис. 1.2 Структурная схема модели Солоу

Структурную схему, представленную на рис. 1.2, можно перестроить с управленческой точки зрения. В самом деле, в реальной экономике одним из наиболее важных рычагов управления являет­ся распределение ВВП на накопление (валовые инвестиции) и по­требление. Поэтому статическое распределительное звено (второе уравнение (1.1.1)) на самом деле можно рассматривать как управ­ляющее. Подобный вариант структуры показан на рис. 1.3. На этой схеме первое и третье звенья вместе образуют объект управления, второе (распределительное) звено играет роль управляющего, а вы­ход четвертого звена L_t служит входом в систему, выходом которой является потребление C_t. Сама система из управляемого объекта и управляющего звена выделена пунктиром.

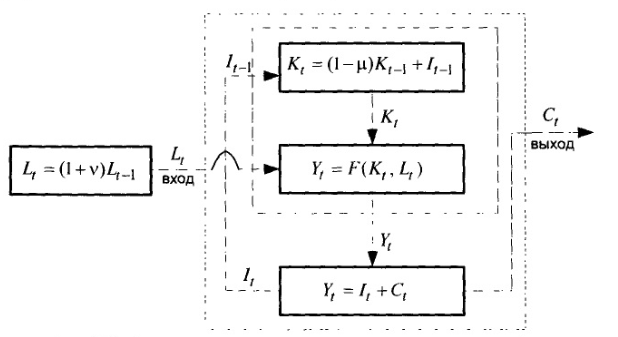
Рис. 1.3. Скорректированная структурная схема модели Солоу

Модель Солоу с непрерывным временем. Предположим теперь, что время, измеряемое вначале с дискретностью в один год, будет из­меряться с дискретностью 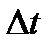(например, полугодие, квартал, месяц, декада, день). При дискретности в один день время можно считать практически непрерывным.

При дискретности 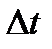модель Солоу будет выглядеть следующим образом:

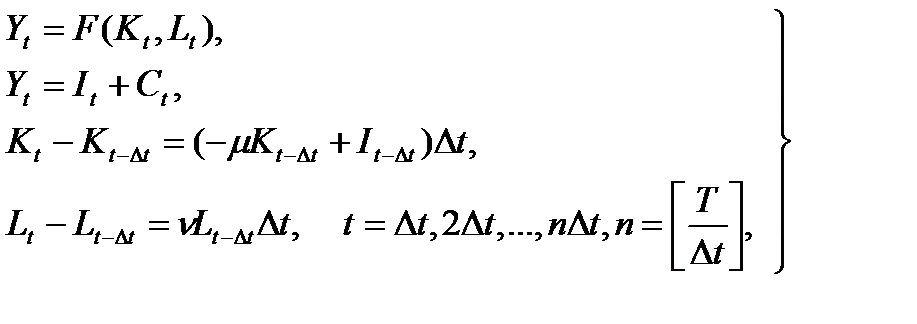(1.1.2)

где Y_t, I_t, C_t — соответственно ВВП, инвестиции и потребление за год, начинающийся в момент t;

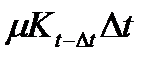—выбытие фондов за время ();

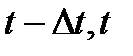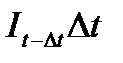—инвестиции за время ();

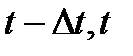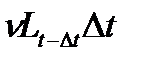— прирост числа занятых за время ().

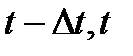При переходе к пределу при 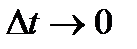уравнения (1.1.2) принимают следующую форму (уравнения модели Солоу с непрерывным временем):

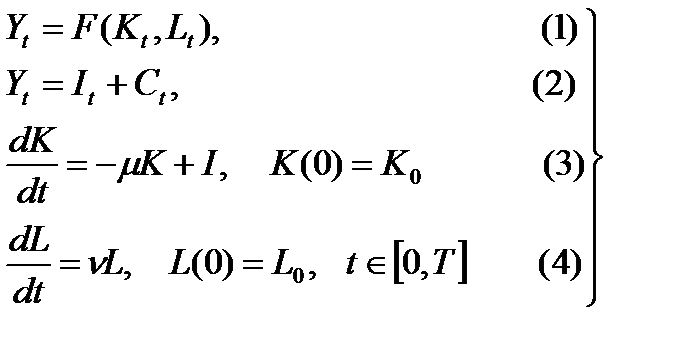(1.1.3)

Данная модель может быть представлена в такой же структурной форме, как это показано на рис. 1.2, 1.3, однако при этом уравнения (3), (4) (1.1.1) должны быть заменены уравнениями (3), (4) (1.1.3).

Следует отметить, что модель Солоу в дискретной форме (1.1.1) имодель Солоу в непрерывной форме (1.1.3),несомненно, являют­ся разными моделями и расчеты по ним приводят к разным, однако достаточно близким, результатам. ►

Как видно из примера 1.1, экономические динамические системы могут быть представлены в форме конечно-разностных уравне­ний (дискретное время) и в форме дифференциальных уравнений (непрерывное время). Между математическими методами диффе­ренциальных и конечно-разностных уравнений нет существенного различия: при решении дифференциальных уравнений на ЭВМ их приближенно заменяют на конечно-разностные; напротив, любое конечно-разностное уравнение можно приближенно заменить диф­ференциальным.

З а м е ч а н и е. При характеристике модели Солоу обычно го­ворят, что в ней экономика представляет собой неструктурирован­ное целое и производит один агрегированный продукт, который может как потребляться, так и инвестироваться. Данное утвержде­ние можно интерпретировать как представление экономики в виде одного динамического элемента (ведь экономика неструктурированна!).

Однако при более детальном знакомстве с моделью (как это сле­дует из примера 1.1) становится ясно, что экономика в форме мо­дели Солоу состоит из четырех элементов, объединенных в контур обратной связи. Кроме того, экономика нелинейна, поскольку связь между выпуском и затратами ресурсов задается в виде нелинейной производственной функции.

Таким образом, даже агрегированное модельное представление экономики позволяет сделать вывод о том, что она является слож­ной динамической системой.

Дата добавления: 2015-06-04