Инерционное звено

Инерционное звено задается дифференциальным уравнением первого порядка

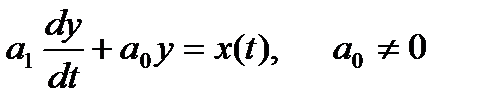(1.2.2)

Уравнение (1.2.2) можно привести к стандартному виду путем деления его на а₀:

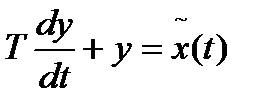, (1.2.3)

где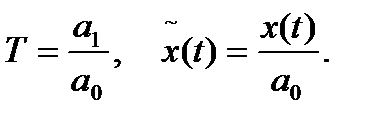

(Содержательный смысл постоянной времени T будет выяснен ниже.)

Инерционное звено описывает процесс «отработки» заданного входного воздействия x(t) (значок «-» опустим), таким образом, что скорость «отработки» пропорциональна разности между входом и выходом:

Пример 1.2. Модель освоения введенных производственных мощностей. Обозначим через x (x= const) введенную производственную мощность, а через y(t) – фактическое производство на базе этой мощности в момент t (фактическое использование мощности, ). Сделав предположение, что прирост производства пропор­ционален недоиспользованной мощности:

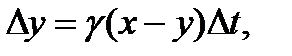
приходим к уравнению инерционного звена:

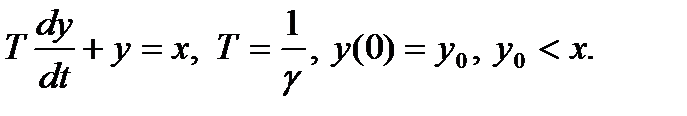(1.2.4)

В соответствии с теорией линейных дифференциальных уравнений (см. Приложение 1) общее решение неоднородного уравнения есть сумма общего решения однородного уравнения и частного ре­шения неоднородного.

Общее решение однородного уравнения

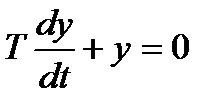(1.2.5)

имеет вид:

у = се^λt.

Подставив его в (1.2.5), получим:

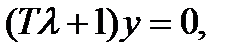
но 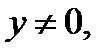поэтому приходим к характеристическому уравнению (от­носительно К):

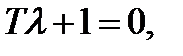или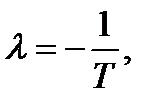

Поскольку частным решением неоднородного уравнения (1.2.4) является у = x, то общее решение этого уравнения примет вид:

.

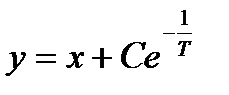Константу С находим из начального условия

, ,

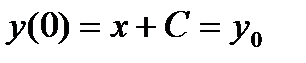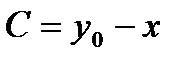поэтому окончательно имеем

.

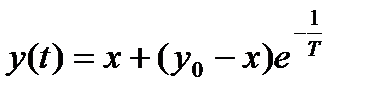Переходный процесс освоения производственных мощностей, описываемый этим решением, завершается выходом на заданный размер мощности

.

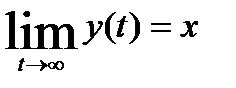Общая картина переходного процесса показана на рис. 1.4

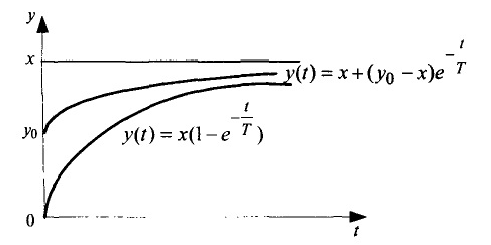
Рис. 1.4. Переходный процесс освоения производственных мощностей

При 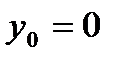решение примет вид:

,

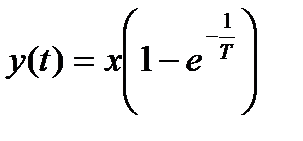поэтому 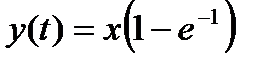, т.е. постоянную времени T можно определить как длину промежутка времени, в течение которого переходный процесс проходит основную часть (≈2/3) своего пути от 0 до х. ►

Пример 1.3. Модель установления равновесной цены. В модели рассматривается рынок одного товара, время считается непрерыв­ным, спрос d и предложение s линейно зависят от цены:

, , .

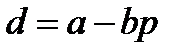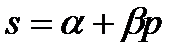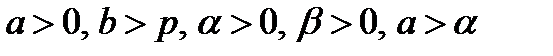Основное предположение модели состоит в том, что изменение цены пропорционально превышению спроса над предложением:

, .

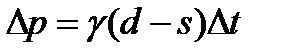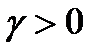т.е, в случае действительного превышения спроса над предложени­ем цена возрастает, в противном случае — падает.

Из основного предположения модели вытекает следующее дифференциальное уравнение для цены:

,

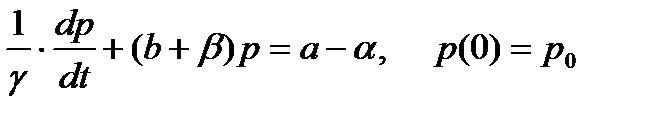т.е. процесс описывается уравнением инерционного звена с 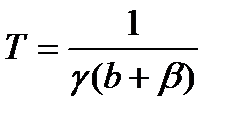и 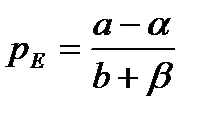, где p_E — равновесная цена (точка пересечения прямых спроса и предложения). Таким образом, цена как выход инерционного звена ведет себя так, как это показано на рис. 1.4 ►

Дата добавления: 2015-06-04