Колебательное звено

Колебательное звено задается дифференциальным уравнением второго порядка

(1.2.11)

с отрицательным дискриминантом, составленным из коэффициентов в левой части уравнения (1.2.11) .

Колебательное звено описывает циклические процессы в эко­номике.

Пример 1.4. Однономенклатурная система управления запасами как колебательное звено. Пусть и — фактические интенсивности расхода и поступления товара в систему управления запа­сами в момент t. Поскольку интенсивность расхода заранее неиз­вестна, то всегда будет образовываться запас y(t) ( если y(t) > 0, то это действительно запас, y(t) < 0, то это дефицит). Изменение запаса следующим образом связано с интенсивностями расхода и поставок:

, или . (1.2.12)

Управлять интенсивностью поставок можно только по известно­му значению запаса y(t) (ведь интенсивность расхода неизвестна!).

Имеется два варианта управления:

1) изменение поставок пропорционально (с обратным знаком) величине запаса (при положительном запасе интенсивность поставок уменьшается, при отрицательном — увеличивается):

, ;

2) изменение интенсивности поставок пропорционально (с об­ратным знаком) как запасу, так и скорости его изменения:

, , ,

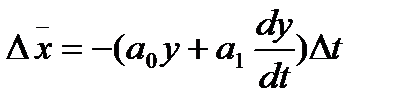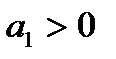(при положительном запасе интенсивность поставок уменьшается, при отрицательном — увеличивается, при положительной скорости роста запаса интенсивность поставок уменьшается, при отрицатель­ной — увеличивается).

П е р в ы й с л у ч а й. Взяв производную от обеих частей (1.2.12)

и подставив в это выражение , получаем дифференциальное уравнение второго порядка для запаса:

. (1.2.13)

Это уравнение колебательного звена с а₂=1, a₁=0 и дискриминантом d=-4a₀<0. Характеристическое уравнение имеет вид (подставляем в однородное уравнение y=Сe^λt):

λ²+a₀=0.

Его корни взаимно сопряженные мнимые:

, , .

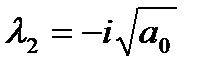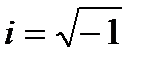Пусть на вход системы, находившейся в начальный' момент в состоянии равновесия x=0, у=0, y'(0)=0, начали поступать заявки на товар с интенсивностью x(t)=x= const. Таким образом, интен­сивность расхода можно представить в виде графика, показанного на рис. 1.5.

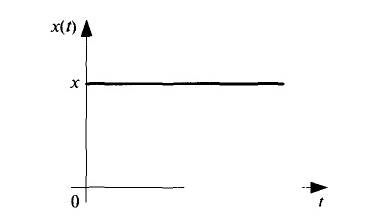
Рис. 1. 5 Интенсивность расхода

Или алгебраически:

где χ(t) – Функция Хэвисайда.

Производная от функции Хэвисайда равна обобщенной функ­ции Дирака δ(t), которая принимает бесконечно большое значение в точке t=0, равна нулю при t≠ 0 и .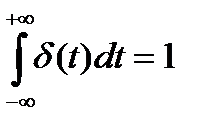

Поскольку

,

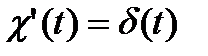то в этой ситуации , и уравнение (1.2.13) принимает вид:

, y(0)=0, y’(0)=0 (1.2.14)

Решим это уравнение операторным методом, применив преоб­разование Лапласа к обеим частям уравнения:

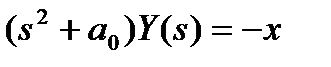, (1.2.15)

где — преобразование Лапласа выхода y(t);

— преобразование Лапласа от правой части (12.15),

поскольку ,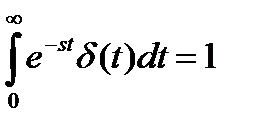

Из (1.2.15) находим преобразование Лапласа выхода y(t):

, .

И, наконец, по табл. 1.1 восстанавливаем выход:

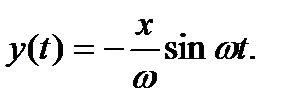
Таким образом, в первом случае при постоянной интенсивности расхода x запас y(t) будет испытывать незатухающие гармонические колебания с амплитудой (рис. 1.6).

При таких незатухающих колебаниях промежутки, когда имеет­ся действительный запас y(t)> 0, будут чередоваться с промежутка­ми дефицита y(t)<0, что крайне отрицательно скажется на финан­совом положении организации, отвечающей за систему управления запасами. Для того чтобы система управления запасами снова во­шла в состояние равновесия, необходимо учитывать не только величину запаса у(t), но и скорость его изменения , как это и предусмотрено во втором случае.

Рис. 1.6. Поведение запаса при поставке, пропорциональной запасу

В т о р о й с л у ч а й. Снова, как и в первом случае, берем про­изводную от обеих частей (1.2.12) и подставляем в это выражение . Получаем дифференциальное уравнение второго порядка для запаса:

(1.2.16)

Уравнение (1.2.16) отличается от (1.2.13) наличием в левой час ти члена , пропорционального скорости изменения запаса.

Характеристическое уравнение имеет вид:

.

Его корни взаимно сопряженные комплексные с отрицательной действительной частью:

, ,

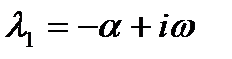где , .

Если с момента времени t = 0 на вход системы стали поступать заявки на товар с постоянной интенсивностью x(t)=x= const, то уравнение (1.2.16), описывающее поведение системы, принимает вид

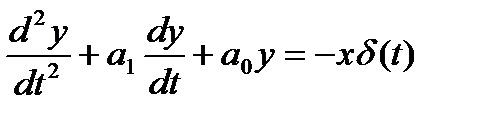, y(0)=0, y’(0)=0. (1.2.17)

Снова решим это уравнение операторным методом. Имеем:

,

откуда

.

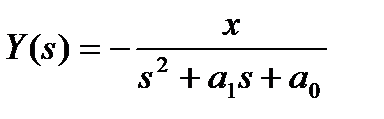Представив в виде , где , , из табл. 1.1 находим

.

Таким образом, поведение запаса описывается затухающими гармоническими колебаниями с амплитудой 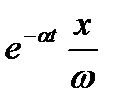, график которых приведен на рис. 1.7. ►

Рис. 1.7. Поведение запаса при поставке, пропорциональной запасу и скорости его изменения

Дата добавления: 2015-06-04