Передаточная функция

Понятие передаточной функции динамического элемента связа­но с операторным методом решения дифференциального уравнения. Суть метода состоит в сведении решения дифференциального урав­нения к решению алгебраического уравнения. В основе метода — переход от первоначальных функций времени х(t), y(t) к их образам X(s), Y(s) — преобразованиям Лапласа этих функций. Необходимые сведения о преобразованиях Лапласа даны в Приложении 1, здесь же напомним только определение преобразования Лапласа для не­которой функции f(t):

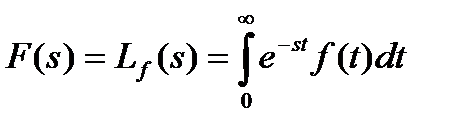, (1.2.7) а также формулу обратного перехода от образа к прообразу:

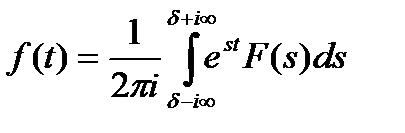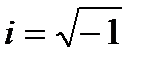, (1.2.8)

Образ производной можно найти по образу функции:

,

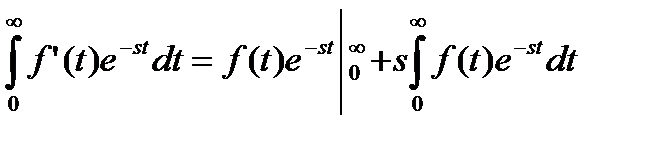поэтому

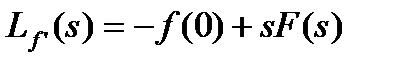. (1.2.9)

.

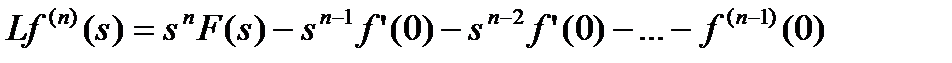В частности, при f (0) =0, .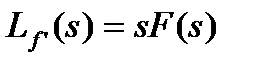

При , .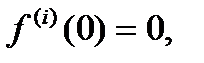

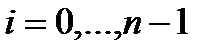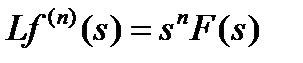В табл. 1.1 приведены преобразования Лапласа некоторых

функций.

Таблица 1.1. Преобразования Лапласа типовых функций

f(t), t> 0	F(s)
δ(t)	1
χ(t)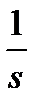
t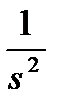

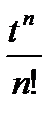
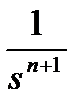
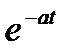
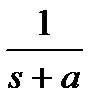
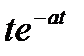
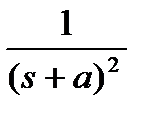
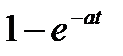
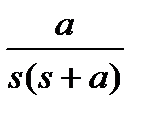
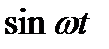
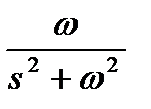
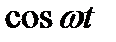
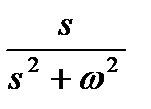
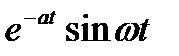
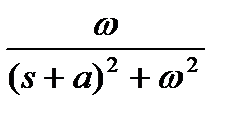
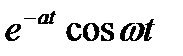
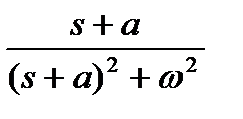
Применим преобразование Лапласа к обеим частям уравнения динамического элемента (1.2.1) (пользуясь формулой (1.2.9) для об­раза производных):

,

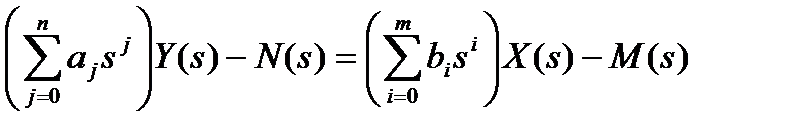где ,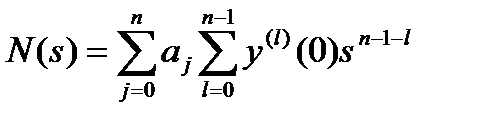

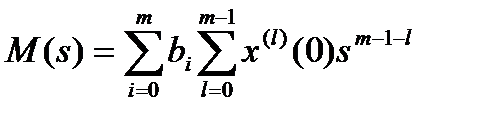
откуда

Y(s) = G(s)X(s)+R(s), (1.2.10)

где , ,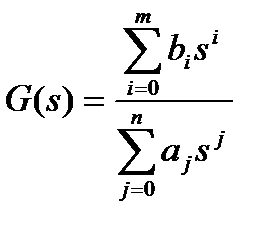

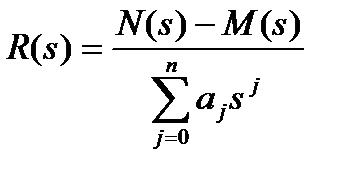R(s)= 0 при 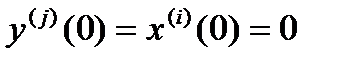, j=0,1,…,n-1, i=0,1,…,m-1

Передаточной функцией G(s) динамической системы (подсистемы, элемента) называется отношение образа выхода к образу входа при нулевых условиях.

Из (1.2.10) видно, что передаточная функция линейного дина­мического элемента является дробно-рациональной функцией па­раметра s. Например, передаточная функция инерционного звена равна (см. (1.2.3))

.

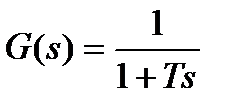В передаточной функции динамической системы (подсистемы, звена) содержатся все сведения о ее поведении при нулевых на­чальных условиях. В самом деле, по входу x(t) находим его образ X(s), затем умножаем этот образ на передаточную функцию, тем са­мым получаем образ выхода Y(s) = G(s)X(s) и, наконец, пользуясь либо табл. 1.1, либо непосредственно формулой (1.2.8), определяем выход y(t). Если начальные условия ненулевые, то к этому решению еще добавится «шлейф», образ которого — R(s).

Дата добавления: 2015-06-04