Колебания и волны

1.1 Механические гармонические колебания.

· Уравнение гармонических колебаний и его решение:

^*,

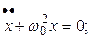
где х – значение колеблющейся величины в момент времени t; А – амплитуда колебаний (максимальное значение колеблющейся величины); – фаза колебаний в момент времени t; 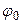– начальная фаза в момент времени t =0; ω ₀ – собственная циклическая частота колебаний.

· Период гармонических колебаний:

; ,

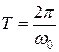где ν – частота колебаний (число полных колебаний в единицу времени).

· Скорость точки, совершающей колебания:

· Ускорение точки, совершающей колебания:

.

Амплитуда скорости и ускорения соответственно равны 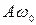и 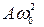. Фаза скорости отличается от фазы смещения на , а фаза ускорения на .

· Сила, под действием которой точка массой m совершает колебания:

,

где 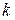– коэффициент упругости, .

· Кинетическая энергия материальной точки, совершающей гармонические колебания:

.

^* В пособии используется функция косинуса.

· Потенциальная энергия материальной точки, совершающей гармонические колебания под действием упругой силы F:

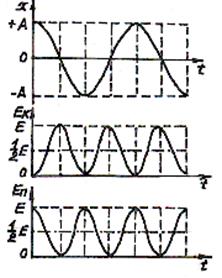
· Полная энергия:

.

На Рис.1 изображены графики зависимости энергий от времени. Энергии 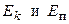изменяются с частотой 2 ω₀, т.е. с частотой, которая в 2 раза превышает частоту изменения х от времени.

Рис.1

1.2 Гармонические осцилляторы: пружинный, физический и математический маятники, колебательный контур (системы, совершающие гармонические колебания).

· Период колебаний пружинного маятника:

,

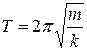где m – масса тела, подвешенного на пружине; k – жесткость пружины.

· Период колебаний математического маятника:

,

где l – длина маятника, g – ускорение свободного падения.

· Период колебаний физического маятника:

= ,

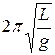где I – момент инерции маятника относительно оси колебаний; m – масса маятника; d – расстояние от центра масс маятника до оси колебаний; - приведенная длина физического маятника.

1.3 Сложение гармонических колебаний.

· При сложении двух одинаково направленных гармонических колебаний одинаковой частоты получается гармоническое колебание той же частоты с амплитудой:

;

и с начальной фазой, определяемой из уравнения:

,

где А₁, А₂ – амплитуды составляющих колебаний; 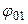, – их начальные фазы.

При сложении колебаний: используют метод вращающего вектора амплитуды, рис.2.

· При сложении двух взаимно перпендикулярных колебаний одинаковой частоты с амплитудами А₁ и А₂ и начальными Рис.2

фазами 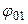, уравнение траектории результирующего движения в координатах x, y имеет вид:

.

1.4 Затухающие колебания.

· Уравнение затухающих колебаний и его решение:

, ,

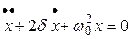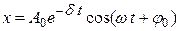где А(t)= – амплитуда затухающих колебаний; А₀ – амплитуда колебаний в момент t =0; δ – коэффициент затухания (); r – коэффициент сопротивления; – циклическая частота затухающих колебаний; ω₀ – собственная циклическая частота свободных незатухающих колебаний той же колебательной системы.

· Время релаксации:

,

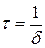где τ – промежуток времени, в течение которого амплитуда затухающих колебаний уменьшится в е раз (е – основание натурального логарифма).

· Логарифмический декремент затухания λ:

,

где A(t), A(t+T) – амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающихся на период; N – число колебаний, совершаемых за время уменьшения амплитуды в е раз.

1.5 Вынужденные колебания.

· Уравнение вынужденных колебаний и его установившееся решение:

; ,

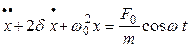где 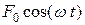– внешняя периодическая сила, действующая на колеблющуюся материальную точку и вызывающая колебания; ω – циклическая частота изменения внешней вынуждающей силы.

· Амплитуда вынужденных колебаний:

.

· Резонанская частота и резонанская амплитуда:

, .

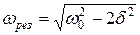1.6 Электромагнитные колебания.

· Уравнение свободных колебаний в идеальном колебательном контуре и его решение:

, ,

где q – заряд на обкладках конденсатора в момент времени t; q_{ma x} – амплитуда колебаний заряда конденсатора с циклической частотой конденсатора ω₀, называемой собственной частотой контура:

,

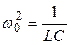и периодом:

- формула Томсона,

где С – емкость конденсатора, L – индуктивность катушки, составляющих колебательный контур.

· Полная энергия идеального колебательного контура:

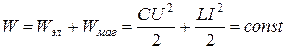
или

,

где С – емкость конденсатора, L – индуктивность катушки, составляющих колебательный контур.

В контуре возникают электрические колебания, сопровождающиеся превращениями энергий электрического 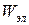и магнитного 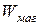полей.

1.7 Свободные затухающие колебания в электрическом колебательном контуре.

· Уравнение затухающих колебаний в контуре и его решение:

,

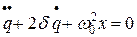
где 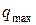– величина заряда на пластинах конденсатора в момент времени t =0; 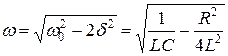- частота затухающих колебаний; - собственная частота; 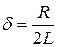- коэффициент затухания.

· Логарифмический декремент затухания:

,

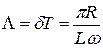где R – активное сопротивление контура; L – индуктивность контура; ω – частота затухания контура.

· Добротность Q контура:

,

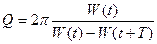где 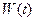- энергия, запасенная в контуре к моменту времени t; - уменьшение энергии за период колебаний Т.

В случае слабого затухания добротность:

.

1.8 Вынужденные электрические колебания.

· Уравнение, описывающее изменения заряда на конденсаторе и установившиеся вынужденные колебания при последовательном включении в контур напряжения :

, ,

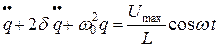где ;

( – сдвиг по фазе между зарядом и приложенным напряжением).

· Сила тока при установившихся колебаниях:

,

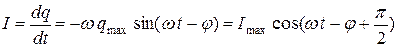где амплитуда тока:

.

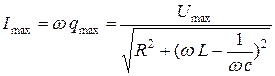Силу тока можно записать в виде:

,

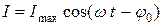где - сдвиг по фазе между током и приложенным напряжением.

Этот сдвиг по фазе находят по формуле:

.

1.9 Упругие (механические) волны – механические возмущения, распространяющиеся в упругой среде.

· Уравнение плоской волны, распространяющейся вдоль положительного направления оси х в однородной непоглощающей среде:

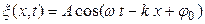
или

,

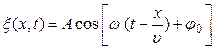где - смещение точек среды с координатой х в момент времени t; А - амплитуда волны; ω – циклическая частота волны; 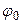– начальная фаза волны (определяется выбором начала отсчета x и t); υ – фазовая скорость; k – волновое число.

· Фаза волны:

.

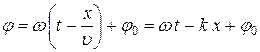· Длина волны:

.

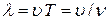· Волновое число:

.

· Волновой вектор – вектор 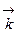, направленный по нормали к волновой поверхности, а модуль, которого равен волновому числу k.

· Уравнение плоской волны, распространяющейся в направлении, определяемом волновым вектором :

.

· Уравнение сферической волны:

,

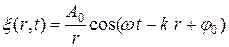где r – расстояние от центра волны до рассматриваемой точки среды. Это уравнение справедливо лишь для r, превышающих размеры источника.

· Фазовая υ и групповая U скорости, а также связь между ними:

; ; .

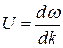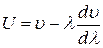· Скорость распространения звуковых волн в газах:

,

где R – универсальная газовая постоянная; µ - молярная масса газа; - отношение молярных теплоемкостей газа при постоянном давлении и объеме; T – термодинамическая температура.

2.0 Электромагнитные волны.

· Уравнения плоской электромагнитной волны:

;

,

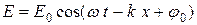где и - соответственно амплитуды напряженностей электрического и магнитного полей волны; ω – циклическая частота; 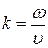- волновое число; 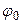– начальная фаза колебаний в точках с координатой х =0.

· Фазовая скорость электромагнитной волны:

,

где - скорость распространения света в вакууме; 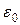и - соответственно электрическая и магнитная постоянные; 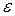и - соответственно электрическая и магнитная проницаемости среды.

· Связь между мгновенными значениями напряженностей электрического Е и магнитного Н полей электромагнитной волны:

.

· Объемная плотность энергии электромагнитного поля:

.

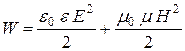· Плотность потока электромагнитной волны – вектор Умова-Пойнтинга:

; ,

где w – объемная плотность энергии волны, 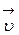- фазовая скорость волны.

· Интенсивность электромагнитной волны I – величина, численно равная энергии, которую переносит волна за единицу времени через единицу площади поверхности, расположенной перпендикулярно к направлению распространения волны:

; ,

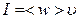где <w> – среднее значение объемной плотности энергии электромагнитного поля волны; 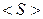- среднее значение модуля вектора Умова-Пойнтинга.

Пример 1. Материальная точка участвует одновременно в двух колебательных процессах, происходящих в одном направлении по гармоническому закону с одинаковой частотой, амплитудами А₁ =5 см и А₂ =10 см и сдвигом по фазе 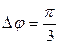. Определить амплитуду и начальную фазу результирующего процесса.

Дано: А₁ =5 см; А₂ =10 см; .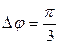

Найти: А; .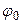

Решение. Законы движения для каждого из процессов могут быть записаны в виде:

, ,

где , 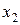- смещения от общего для обоих процессов положения равновесия; ω – циклическая частота. (Поскольку начальная фаза 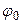определяется выбором начала отсчета времени, можно положить 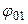=0, = ).

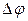Закон движения точки, участвующей в двух колебательных процессах:

, (1)

где x – результирующее смещение точки от положения равновесия.

Поскольку оба колебания гармонические с одинаковой частотой и одного направления, результирующее колебание точки гармоническое с той же частотой и закон движения может быть записан также в виде:

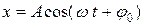, (2)

где А – амплитуда результирующего колебания; 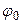– его начальная фаза, равная сдвигу по фазе относительно первого колебания.

Неизвестные А и 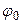могут быть найдены либо аналитическим методом, либо методом векторного сложения колебаний.

Ø Аналитический метод. Согласно уравнений (1) и (2) получим:

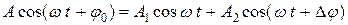. (3)

Используя формулы косинуса суммы двух углов, перепишем уравнение (3):

.

Это уравнение будет тождеством относительно переменной t, если коэффициенты пр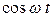и () и (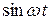) в левой части тождества равны соответствующим коэффициентам в правой части:

; .

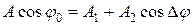Решая эту систему уравнений относительно неизвестных А и 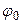, получаем:

;

.

Ø Векторный метод. Любой гармонический процесс можно привести в однозначное соответствие с вращением вектора с угловой скоростью ω, равной циклической частоте колебаний. Модуль вектора равен амплитуде колебаний, угол 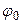, образованный этим вектором с осью ох, равен начальной фазе колебаний. Проекция вектора на ось ох в любой момент времени будет меняться по гармоническому закону:

.

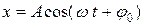При сложении колебаний, происходящих с одинаковой частотой, угол между векторами и 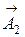не изменяется с течением времени и равен Δφ – разности начальных фаз. Поэтому при сложении таких колебаний все векторы можно показать для момента t =0. Векторы и 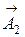показаны на рис.3 (), ().

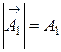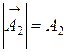Рис.3

Вектор направлен вдоль оси ох, поскольку начало отсчета времени выбрано так, что 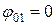. Угол наклона вектора 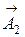к оси ох равен .

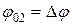Согласно теореме косинусов амплитуда результирующего колебания:

.

Угол наклона вектора к оси ох и будет начальной фазой результирующего колебания:

,

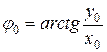причем 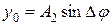, , откуда .

Таким образом, оба метода дают достаточно простые решения задачи.

Выполним вычисления:

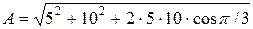=13 см.

=41⁰=0,23 π.

Ответ: А =13 см, 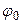=0,23 π.

Пример 2. Математический маятник длины l =50 см совершает небольшие колебания в среде, в которой коэффициент затухания δ =09 с^-1. Определить время τ и число полных колебаний N, по истечении которых амплитуда маятника уменьшится в пять раз. Во сколько раз должен возрасти коэффициент трения, чтобы колебания оказались невозможными?

Дано: l =50 см=0,50 м; δ =09 с^-1.

Найти: τ, N, .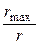

Решение: При отсутствии трения колебания маятника в вертикальной плоскости происходят по гармоническому закону с собственной циклической частотой:

. (1)

Вследствие трения колебания маятника будут затухающими:

,

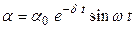где α – угол отклонения нити маятника от вертикали в момент t. (Записанный закон движения соответствует такому началу отсчета времени, что при t =0 маятник проходит через положение равновесия, т.е. α =0).

Период затухающих колебаний:

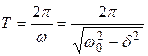, (2)

а амплитуда A затухающих колебаний изменяется со временем по экспоненциальному закону:

. (3)

Запишем выражение (3) для моментов времени t и t+τ:

, .

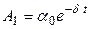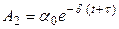Отношение амплитуд 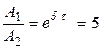. Логарифмируя это выражение, находим

.

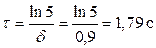Число полных колебаний, прошедших за время τ, равно отношению:

.

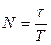Определим из выражения (1) собственную циклическую частоту математического маятника и, подставив её в выражение (2), получим:

.

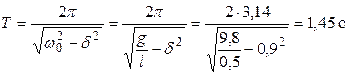Из сравнения T и τ видно, что 1< N <2 (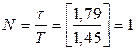), т.е. по прошествии двух полных колебаний амплитуда уменьшится уже больше, чем в 5 раз, что соответствует уменьшению энергии маятника больше, чем в 25 раз (полная энергия колебательного движения маятника пропорциональна квадрату амплитуды, ).

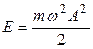Затухающие колебания по записанному выше закону возникают только при условии δ < ω₀ (это очевидно из выражения периода (2): при δ > ω₀ период и циклическая частота оказываются мнимыми величинами). При происходит апериодический процесс.

Предельное значение коэффициента затухания δ, при котором возможны колебания, δ_max = ω₀, причем , где m – масса маятника, постоянная по условию задачи; r – коэффициент трения. Следовательно, искомое значение отношения коэффициентов трения:

.

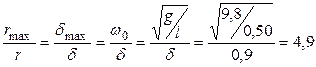Ответ: τ =1,79 с; N =1; 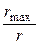=4,9.

Пример 3. В вакууме вдоль оси х распространяется плоская электромагнитная волна. Интенсивность волны, т.е. средняя энергия, проходящая через единицу поверхности за единицу времени, составляет 21,2 мкВт/м². Определить амплитуду напряженности электрического поля волны.

Дано: =1; μ =1; I =21,2 мкВт/м²=2,12×10^-5 Вт/м².

Найти: Е₀.

Решение: Так как интенсивность электромагнитной волны определяется как средняя энергия, проходящая через единицу поверхности за единицу времени, то

, (1)

где < S> – среднее значение модуля вектора плотности потока электромагнитной энергии – вектора Умова-Пойнтинга. Согласно определению,

,

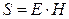где E и H – соответственно мгновенные значения напряженностей электрического и магнитного полей волны, описываемые уравнениями:

;

,

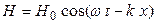где E₀ и H₀ – соответственно амплитуды напряженностей электрического и магнитного полей волны; ω – циклическая частота; k=ω/υ – волновое число (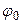 - начальная фаза колебаний принята равной нулю).

Мгновенное значение модуля вектора Умова-Пойнтинга:

,

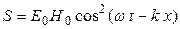а его среднее значение, учтя, что :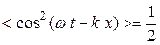

. (2)

В бегущей электромагнитной волне мгновенные значения E и H в любой точке связаны соотношением:

,

откуда (учтя, эта электромагнитная волна распространяется в вакууме):

. (3)

Подставим (3) в (2) и учитывая (1), получим искомую амплитуду напряженности электрического поля волны:

.

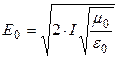Выполним вычисления:

.

Ответ: .

Дата добавления: 2015-06-04